文章标题：《VanillaNet: the Power of Minimalism in Deep Learning》
文章地址：https://arxiv.org/abs/2305.12972
github地址：https://github.com/huawei-noah/VanillaNet

华为诺亚方舟实验室和悉尼大学，2023年5月代码刚开源的文章

---

作者说，在卷积网络中加入人为设计的模块，达到了更好的效果，复杂度也增加了。尽管这些很深很复杂的神经网络被优化得很好，达到了令人满意的性能，但是这给部署带来了挑战。

比方说 ResNets 里的 shortcut 操作大量的芯片内存。另外，像 AS-MLP 的 axial shift 和 Swin Transformer 的 shift window self attention 这些复杂的操作需要复杂的工程实现，包括重写 CUDA 的代码。

而 ResNet 的发展看起来让大家放弃了用纯的卷积层来构造网络。就像 ResNet 它自己说的：没有 shortcut 的普通网络将出现梯度消失，导致 $34$ 层的普通网络性能比 $18$ 层的差。 另外，像 AlexNet 和 VGGNet 这种简单网络的性能被 ResNets 和 ViT 等深度复杂网络所超越，于是更少人花心思去设计和优化简单的网络。

于是提出了 VanillaNet，这是一种新颖的神经网络架构，强调设计的优雅和简单，同时在计算机视觉任务中保持卓越的性能。VanillaNet 通过避免过多的 depth、shortcuts 和复杂的操作（如self-attention）来实现这一点，从而产生了一系列精简的网络，这些网络解决了固有的复杂性问题，非常适合资源有限的环境。

(1)

为了训练这个 VanillaNet，作者对面临的挑战进行了全面分析，并且制定了叫做 “deep training” 的策略。简单来说就是准备好网络之后，在训练的时候逐渐消除卷积层之间的非线性层（激活函数），最后把卷积层也合并成一个。

假设激活函数（通常可以是ReLU或Tanh）表示为 $A(x)$，再结合一个恒等映射（identity mapping），写成如下形式：

$$A^{\prime }(x)=(1-\lambda )A(x)+\lambda x\text{\hspace{1em}(1)}$$
其中 $\lambda$ 是个超参数，用于调整这个函数 $A^{\prime }(x)$ 的非线性能力。

设总的 epochs 数是 $E$，当前是第 $e$ 个 epoch，则 $\lambda =\frac{e}{E}$。

所以开始的时候 $\lambda =0$，这表现为一个完整的激活函数，没有恒等映射。
随着训练的进行，最后 $\lambda =1$，两个卷积之间没有激活函数了。

画个图给你看：

最后把这两层卷积也合并起来，bn层也融合进来，BN融合的公式如下：

代码如下：

    def _fuse_bn_tensor(self, conv, bn):
        kernel = conv.weight
        bias = conv.bias
        running_mean = bn.running_mean
        running_var = bn.running_var
        gamma = bn.weight
        beta = bn.bias
        eps = bn.eps
        std = (running_var + eps).sqrt()
        t = (gamma / std).reshape(-1, 1, 1, 1)
        return kernel * t, beta + (bias - running_mean) * gamma / std

(2)

这么弄了之后，为了增强网络的非线性的能力，又提出了一种有效的，基于级数的激活函数。它包含多个可学习的仿射变换。
原文如下所示：

公式写得很复杂，根据代码的理解，简单来说就是设计了一组卷积核，参数是可学习的，对激活后的数据做一次卷积，再加上BN。
把这些操作包装起来叫做自己的 Activation。画个图给你看：

他说这个实际上比真正的卷积的计算量要小，并且给了一堆证明：

这个 Activation 是作者封装的激活函数，代码如下：

class activation(nn.ReLU):
    def __init__(self, dim, act_num=3, deploy=False):
        super(activation, self).__init__()
        self.act_num = act_num
        self.deploy = deploy
        self.dim = dim
        self.weight = torch.nn.Parameter(torch.randn(dim, 1, act_num*2 + 1, act_num*2 + 1))
        if deploy:
            self.bias = torch.nn.Parameter(torch.zeros(dim))
        else:
            self.bias = None
            self.bn = nn.BatchNorm2d(dim, eps=1e-6)
        weight_init.trunc_normal_(self.weight, std=.02)

    def forward(self, x):
        if self.deploy:
            return torch.nn.functional.conv2d(
                super(activation, self).forward(x), 
                self.weight, self.bias, padding=self.act_num, groups=self.dim)
        else:
            return self.bn(torch.nn.functional.conv2d(
                super(activation, self).forward(x),
                self.weight, padding=self.act_num, groups=self.dim))

    def _fuse_bn_tensor(self, weight, bn):
        kernel = weight
        running_mean = bn.running_mean
        running_var = bn.running_var
        gamma = bn.weight
        beta = bn.bias
        eps = bn.eps
        std = (running_var + eps).sqrt()
        t = (gamma / std).reshape(-1, 1, 1, 1)
        return kernel * t, beta + (0 - running_mean) * gamma / std
    
    def switch_to_deploy(self):
        kernel, bias = self._fuse_bn_tensor(self.weight, self.bn)
        self.weight.data = kernel
        self.bias = torch.nn.Parameter(torch.zeros(self.dim))
        self.bias.data = bias
        self.__delattr__('bn')
        self.deploy = True

VanillaNet 的主要卖点就是以上两个东西。

整体网络很简单，看起来像 VGG 或是 AlexNet：

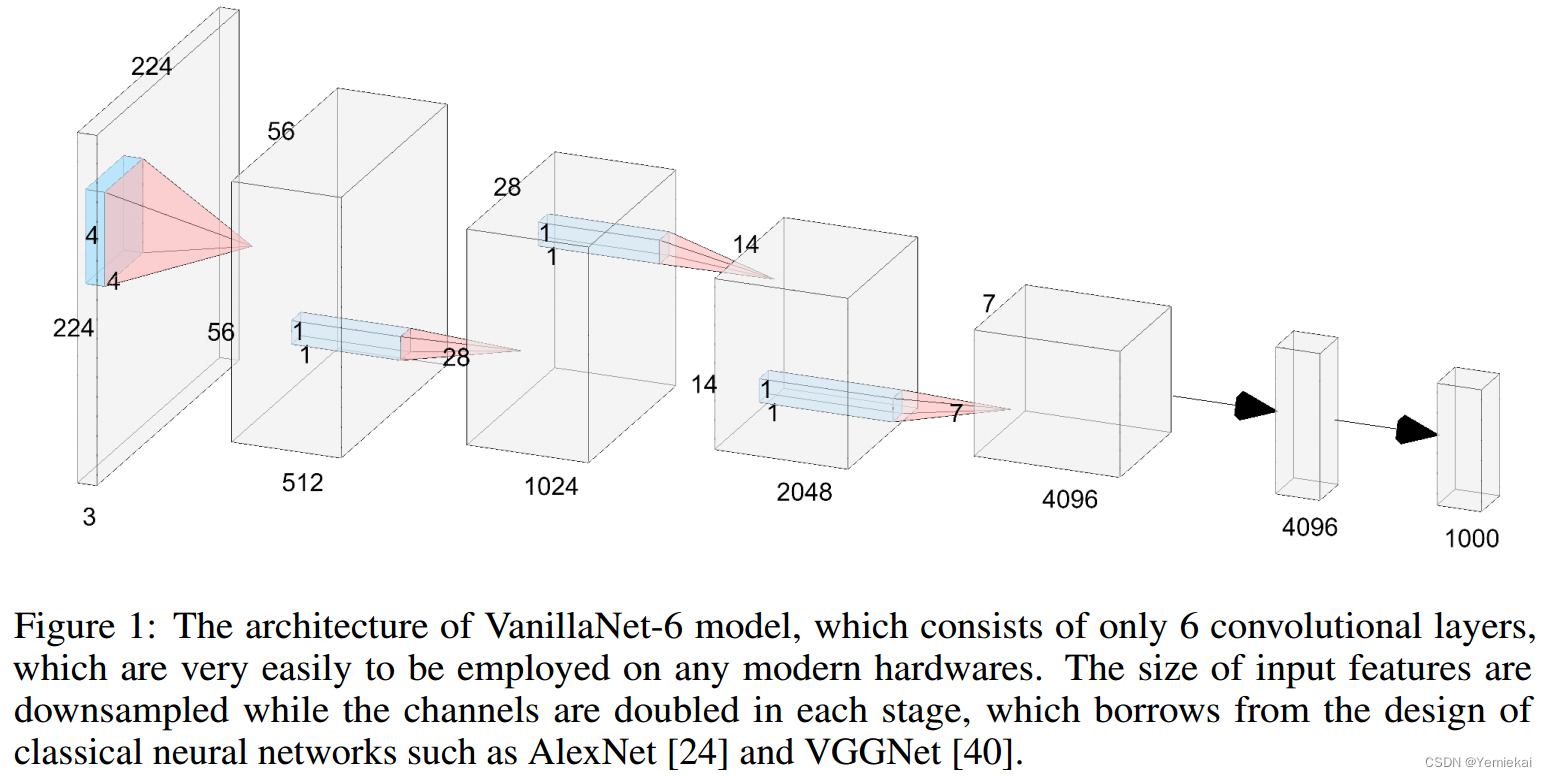
实验部分自己看。