快排
归并排序和快速排序的时间复杂度都是 O(nlogn)
左右两边设置哨兵,分成左边小于x, 右边大于x。
(先分交换, 再递归)
#include<iostream>
using namespace std;
const int N=1e6+10;
int n;
int q[N];
void quick_sort(int q[], int l , int r)
{
if(l>=r)
{
return;
}
int x=q[l],i=l-1,j=r+1; //在两侧, 因为调整的时候,交换之后需要往中间移动。
//以下思路是 先 移动,再交换
while(i<j)
{
do{
i++;
}while(q[i]<x);
do{
j--;
}while(q[j]>x);
if(i<j)
swap(q[i],q[j]);
}
//递归处理左右两边
quick_sort(q, l,j);
quick_sort(q,j+1, r);
}
int main()
{
scanf("%d", &n);
for(int i=0; i<n; i++ )
{
scanf("%d", &q[i]);
}
quick_sort(q,0,n-1);
for(int i=0; i<n; i++ )
{
printf("%d,", q[i]);
}
}
为什么说快速排序一般优于归并排序?
quicksort通常比其他排序算法快得多,因为它在原地运行,而不需要创建任何辅助数组来保存临时值。与merge sort相比,这是一个巨大的优势,因为分配和释放辅助数组所需的时间是显而易见的。就地操作也提高了quicksort的位置。
练习题 https://www.acwing.com/problem/content/788/
快速选择 算法的时间复杂度是 O(n)
只需要递归一边即可,不需要两边都排好,这样时间复杂度就降下来了。

具体需要的时间就是:

第k 个 数

快速选择算法
#include<iostream>
#include<vector>
using namespace std;
const int N=1e6+10;
int n, k;
int q[N];
int quick_sort(int left, int right,int k)
{
if( left == right ) // 一定 在 区间 里 面
{
return q[left];
}
int x=q[left], l = left-1, r=right+1;
while( l < r )
{
do
{
l++;
}while(q[l]<x);
do
{
r--;
}while(q[r]>x);
if(l < r)
{
swap(q[l],q[r]);
}
}
int sl = r - left + 1 ; // 计算 左 边 一共 有几个 数 字 。
if(k <= sl ) // 在 左半边
return quick_sort(left, r, k); // 注意是 return, 需要返回值的。
return quick_sort( r+1,right, k-sl ); // 剩下的右半边 里面是 第 k-sl 个
}
int main()
{
cin >> n >> k ;
for( int i=0 ; i < n ; i++ )
{
cin>>q[i];
}
int s=quick_sort(0,n-1,k);
cout<<s ;
return 0;
}
归并排序 (分治) 时间复杂度 : nlogn
以数组的中心为分, 分成左边和右边。
① 确定分届点,mid= (left + right)/ 2
② 递归 left,right。
③ 归并—— 合二为一
在两半之中,找较小者。 小的那个 就 拿出来, 最后剩下的 就直接接在后面。

往后挪就行。 归并排序是稳定的。

时间复杂度 : nlogn
下面列举可以发现。每一层都是 n, 一共 logn(2为底数)层。
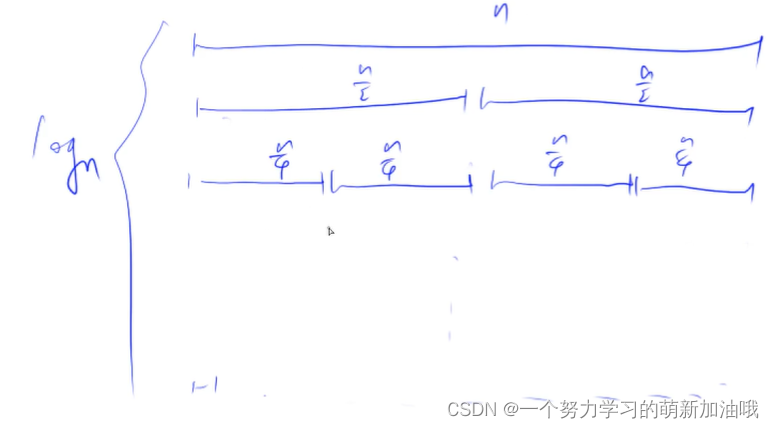
代码模板
#include<iostream>
using namespace std;
const int N=1e6+10;
int n;
int q[N],temp[N];
void merge_sort(int q[], int l , int r)
{
if(l>=r) return;
int mid= l+r >> 1;
merge_sort(q, l,mid);
merge_sort(q,mid+1, r);
int k=0 , i=l , j=mid+1; // i是 左边界, j 是 右半边的开始位置。
while(i<=mid && j<=r)
{
if(q[i]<=q[j]) // 取小的那个
temp[k++]=q[i++];
else
temp[k++]=q[j++];
}
//以上已经排好一半的序了
while(i<=mid) //左半边没有循环结束
temp[k++]=q[i++];
while(j<=r) //右半边没有结束 ,r是右边界
temp[k++]=q[j++];
//循环结束,需要把 数据 复制一遍过去。
for( i=l, j=0 ; i<=r ; i++, j++ )
{
q[i]=temp[j];
}
}
int main()
{
scanf("%d", &n);
for(int i=0; i<n; i++ )
{
scanf("%d", &q[i]);
}
merge_sort(q , 0 , n-1 );
for(int i=0; i<n; i++ )
{
printf("%d,", q[i]);
}
}
归并排序的拓展 —— 求逆序对的数量https://www.acwing.com/problem/content/790/
逆序对: 前面的数 比后面的数大, 则是逆序对。

二分
整数二分
二分的本质不是单调性。
要符合一些条件。

bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
作者:yxc
链接:https://www.acwing.com/blog/content/277/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
二分法的实际操作练习
https://www.acwing.com/problem/content/791/
答案
#include<iostream>
using namespace std;
const int N=1e6+10;
int n, m ;
int q[N];
int main()
{
scanf("%d%d", &n,&m);
for(int i=0; i<n; i++ )
{
scanf("%d", &q[i]);
}
while(m--)
{
int x;
scanf("%d", &x);
int l = 0 ,r = n-1;
while(l < r)
{
int mid= l+r>>1;
if(q[mid]>=x) r=mid;
else
l=mid+1;
}
if(q[l]!=x)//没有找到
cout<<"-1 -1"<<endl;
else
{
cout<<l<<' ';
int l=0, r=n-1;
while( l < r)
{
int mid = l + r +1 >>1;
if(q[mid] <= x) l=mid;
else r=mid-1;
}
cout<<l<<endl;
}
}
return 0;
}
浮点数二分
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
高精度大数加法

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
作者:yxc
链接:https://www.acwing.com/blog/content/277/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
高精度大数减法
A-B
这里默认A> B
如果A< B 那么计算-(B-A)
减法
如果本位不够,向后借位。
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t; //减去之前的借位。
if (i < B.size()) t -= B[i];//B[i]要存在才能减去
C.push_back((t + 10) % 10);
if (t < 0) t = 1; //有结位。
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
作者:yxc
链接:https://www.acwing.com/blog/content/277/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

高精度乘低精度 —— 模板题 AcWing 793. 高精度乘法
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b; // b 这里 是整个 乘进来。
C.push_back(t % 10);//尾部添加、
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();// 删除多余的0,//尾端删除元素
return C;
}
作者:yxc
链接:https://www.acwing.com/blog/content/277/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
例题案例
#include<iostream>
#include<vector>
using namespace std;
const int N=1e6+10;
string n;
int m;
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b; // b 这里 是整个 乘进来。
C.push_back(t % 10); //尾部添加
t /= 10;
}
while (C.size() > 1 && C.back() == 0)
C.pop_back(); // 删除多余的0,//尾端删除元素
return C;
}
int main()
{
cin>>n>>m;
//
// vector<int>s= mul(n,m);
vector<int> A;
string k=n;
for(int i=n.size()-1; i>=0; i--)
A.push_back(n[i]-'0');
vector<int> c= mul(A,m);
for(int i=c.size()-1; i>=0; i--)
cout<<c[i];
return 0;
}
高精度除法
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
作者:yxc
链接:https://www.acwing.com/blog/content/277/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
前缀和
原数组 : A1, A2, A3, A4, A5…AN
前缀和: Si=A1+ A2+ A3+A4+…+Ai
a[l] + … + a[r] = S[r] - S[l - 1]
定义 S【0】=0
这样下标计算就合理了。
练习题 795. 前缀和https://www.acwing.com/problem/content/797/
输入格式
第一行包含两个整数 n和 m。
第二行包含 n 个整数,表示整数数列。
接下来 m 行,每行包含两个整数 l 和 r,表示一个询问的区间范围。
输出格式
共 m 行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,1≤n,m≤100000, −1000≤数列中元素的值≤1000
#include<iostream>
#include<vector>
using namespace std;
const int N=1e6+10;
int n, m;
int q[N];
int S[N+1];
int main()
{
cin >> n >> m ;
S[0]=0;
for( int i=0 ; i < n ; i++ )
{
cin>>q[i];
S[i+1]=S[i]+q[i];
}
int l,r ;
for(int i = 0 ; i < m ; i ++ )
{
cin >> l >> r ;
cout<<S[r]-S[l-1]<<endl;
}
return 0;
}
二维前缀和
前缀是两个方向的前缀。
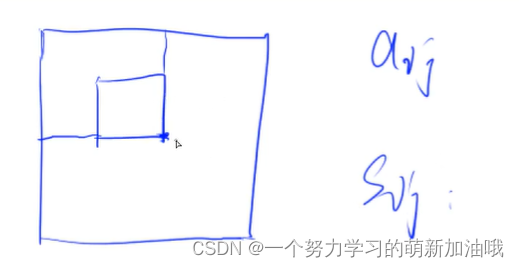
求以(x1, y1) 和(x2, y2 )的正方形的面积
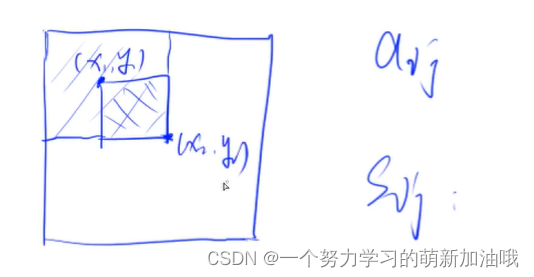
用面积减法完成
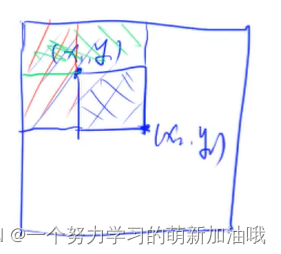
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
差分
有数组 a1, a2, a3, … an
构造 数组 b1, b 2, b3, … bn
使得 ai = b1+ b2+ b3+… . + bi (前缀和)
这里 bi 就是 a数组的 差分, 而 a数组 就是 b数组 的前缀和
给区间[l, r]中的每个数加上c:只需要: B[l] += c , B[r + 1] - = c
下面是证明思路:
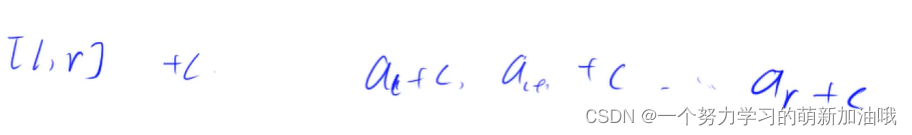
给 b[l] 加上c , 则可以发现 al = b1+ b2+ b3+… . + bl 也加上了 C
可以发现 a(l+1) = b1+ b2+ b3+… . + b(l+1) 也很明显加上了 c 。
因为给的区间是 [l, r] 这个区间, 所以到 a(r+1)的位置 都加上了 c 。
这里需要把 b(r+1) -=c 才能让 a(r+1)还是原来的数。
所以这里是差分的思路。
练习

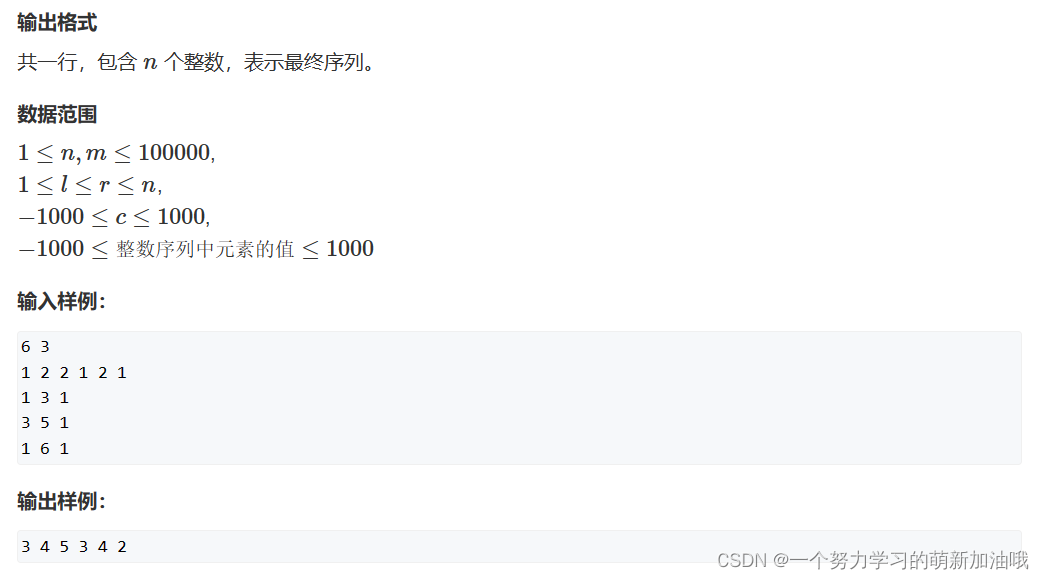
直接用公式即可。 不难。
二维差分 —— 模板题 AcWing 798. 差分矩阵
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
一旦S[x1, y1] += c 之后, 会发现 右下角所有都加上了c,
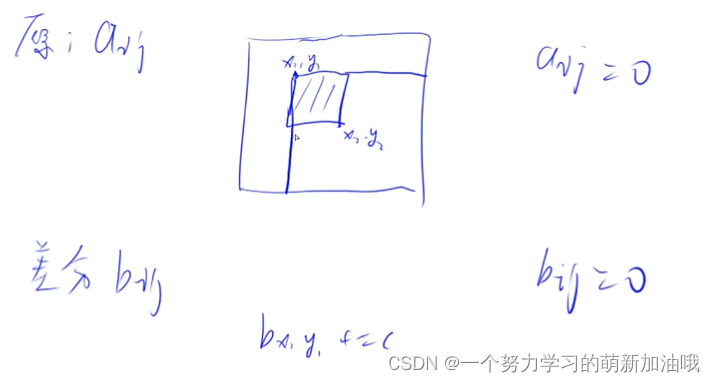
把不应该加上c 的位置 ,减去c
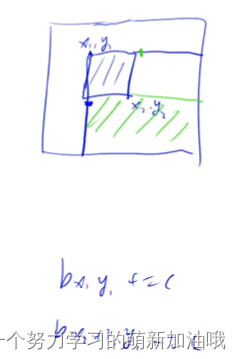
再减去该减的位置
S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c
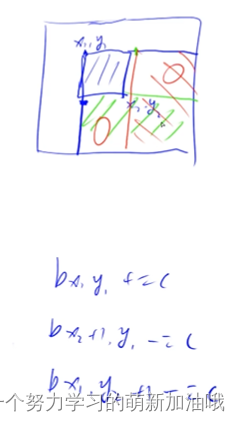
有一块多减了一次,所以 加上 S[x2 + 1, y2 + 1] += c
练习 题 https://www.acwing.com/problem/content/800/
双指针算法
位运算
求n的第k位数字: n >> k & 1
lowbit树状数组的一个操作。
lowbit(x)返回x 的最后一个 1
返回n的最后一位1:lowbit(n) = n & -n
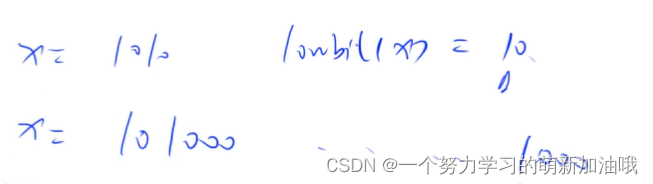
注意计算机中的负数 是用补码来表示的。
因为-x= ~x +1
负x= 取反x +1
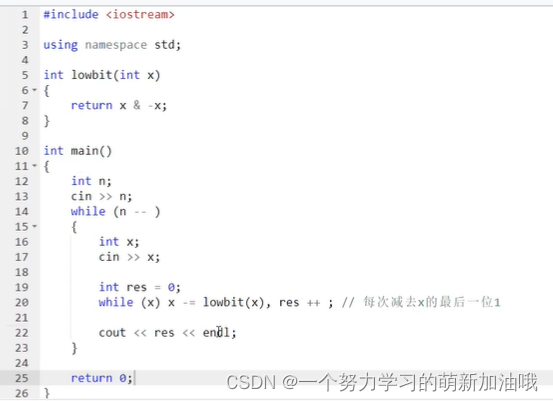
lowbit(x)可以判断x中有几个1 存在
二进制中1的个数
给定一个长度为 n
的数列,请你求出数列中每个数的二进制表示中 1 的个数。
输入格式
第一行包含整数 n。
第二行包含 n 个整数,表示整个数列。
输出格式
共一行,包含 n 个整数,其中的第 i 个数表示数列中的第 i 个数的二进制表示中 1 的个数。
数据范围
1≤n≤100000, 0≤数列中元素的值≤109
输入样例:
5
1 2 3 4 5
输出样例:
1 1 2 1 2
离散化
离散化本质上是一种哈希,它在保持原序列大小关系的前提下把其映射成正整数。
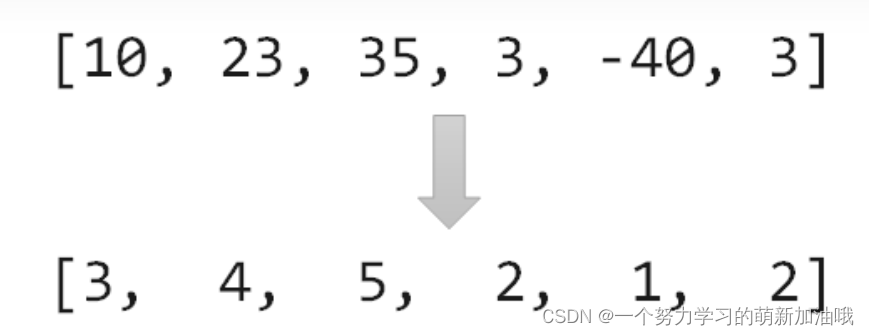
练习题
区间和

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}
作者:yxc
链接:https://www.acwing.com/blog/content/277/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 300010; //n次插入和m次查询相关数据量的上界
int n, m;
int a[N];//存储坐标插入的值
int s[N];//存储数组a的前缀和
vector<int> alls; //存储(所有与插入和查询有关的)坐标
vector<pair<int, int>> add, query; //存储插入和询问操作的数据
int find(int x) { //返回的是输入的坐标的离散化下标
int l = 0, r = alls.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
int x, c;
scanf("%d%d", &x, &c);
add.push_back({x, c});
alls.push_back(x);
}
for (int i = 1; i <= m; i++) {
int l , r;
scanf("%d%d", &l, &r);
query.push_back({l, r});
alls.push_back(l);
alls.push_back(r);
}
//排序,去重
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
//执行前n次插入操作
for (auto item : add) {
int x = find(item.first);
a[x] += item.second;
}
//前缀和
for (int i = 1; i <= alls.size(); i++) s[i] = s[i-1] + a[i];
//处理后m次询问操作
for (auto item : query) {
int l = find(item.first);
int r = find(item.second);
printf("%d\n", s[r] - s[l-1]);
}
return 0;
}
作者:liangshang
链接:https://www.acwing.com/solution/content/13511/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
区间合并
给定 n个区间 [li,ri],要求合并所有有交集的区间。注意如果在端点处相交,也算有交集。输出合并完成后的区间个数。
例如:[1,3] 和 [2,6] 可以合并为一个区间 [1,6]
输出: 合并区间完成后的区间个数。
思路:
第一步: 按区间左端点排序
第二步: 扫描整个区间,把可能的交集合并。
维护一个区间。

第二种情况, 把区间变长,ed往后挪、
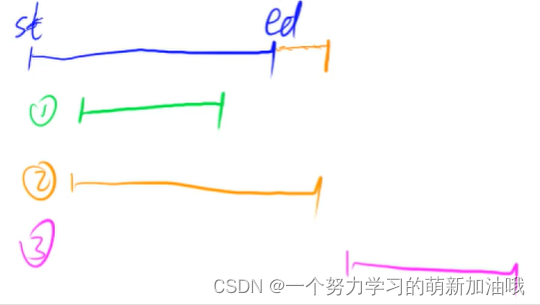
练习题:803. 区间合并 https://www.acwing.com/problem/content/805/
给定 n个区间 [li,ri],要求合并所有有交集的区间。注意如果在端点处相交,也算有交集。输出合并完成后的区间个数。
例如:[1,3] 和 [2,6] 可以合并为一个区间 [1,6]
输出: 合并区间完成后的区间个数。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N=1e6+10;
int n;
int q[N];
typedef pair<int ,int >PII; // 存一个 数对
vector<PII> segs;
void merge(vector<PII> &s)
{
vector <PII> news;
sort(s.begin(),s.end()); //优先左端点排序。
int st =-2e9, ed= -2e9;
for(auto seg : s)
{
if(ed< seg.first)//没有交集,就是需要维护的区间, 更新s, ed
{
if(st!=-2e9)//新区间
{
news.push_back({st,ed});
}
st=seg.first,ed=seg.second;
}
else
{
ed=max(ed, seg.second); //取 大的 那个 更新 即可。
}
}
if(st != -2e9) news.push_back({st,ed});
s=news;
}
int main()
{
cin >> n ;
int l,r;
for(int i=0; i<n;i++)
{
cin>>l>>r;
segs.push_back({l,r});
}
merge(segs);
cout<<segs.size()<<endl;
return 0;
}





![[BigGAN] Large Scale GAN Training for High Fidelity Natural Image Synthesis](https://img-blog.csdnimg.cn/be48b3fd3c264c20ba953a95f6c787ae.png)