[论文阅读] 颜色迁移-Automated Colour Grading
文章: Automated colour grading using colour distribution transfer, [paper], [matlab代码], [python代码]
1-算法原理
本文算法分为2个大步骤, 首先使用IDT(Iterative Distribution Transfer)方法得到初步的结果, 这个结果里面可能会将噪声放大了, 因而第二大步是进行后处理, 减少伪影, 保留原图的梯度.
具体地:
- IDT方法, 得到初始结果, 详细原理可以查看本文描述, 也可以查看作者的另外一篇文章 N-Dimensional Probability Density Function Transfer and its Application to Colour Transfer, 或者也可以查看这篇博客 [论文阅读] 颜色迁移-N维pdf迁移
- 后处理, 减少伪影, 保留原图的梯度, 如下所示, 本文使用优化方法,
J
J
J为最后需要得到的图像,
I
I
I为原图,
t
(
I
)
t(I)
t(I)为第一步IDT结果,
∇
\nabla
∇表示梯度计算,
ϕ
\phi
ϕ 和
ψ
\psi
ψ 分别为权重系数
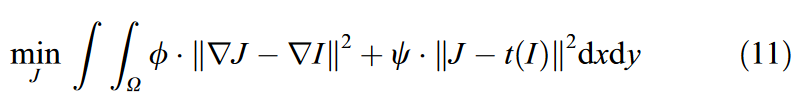
上述公式中, 第一部分用来保留梯度, 如果仅有这部分, 最后的结果就是原图, 第二部分用来保证与目标图像颜色接近.
2-算法核心
第一部分这里不再说明, 详见 [论文阅读] 颜色迁移-N维pdf迁移.
对于第二部分, 文中进行了简单化调整, 过程如下, 这里直接复制文中的说明, 数学不好就不做解释了

公式局部可能写错了, 根据作者提供的代码实现进行调整并简化, 保持公式与代码实现保持一致, 方便理解, 如下所示:
I 0 = I ( x , y ) I 1 = I ( x , y − 1 ) I 2 = I ( x , y + 1 ) I 3 = I ( x − 1 , y ) I 4 = I ( x + 1 , y ) J 0 = J ( x , y ) J 1 = J ( x , y − 1 ) J 2 = J ( x , y + 1 ) J 3 = J ( x − 1 , y ) J 4 = J ( x + 1 , y ) \begin{aligned} &I_0 = I(x,y)\\ &I_1 = I(x,y-1)\\ &I_2 = I(x,y+1)\\ &I_3 = I(x-1,y)\\ &I_4 = I(x+1,y)\\ &J_0 = J(x,y)\\ &J_1 = J(x,y-1)\\ &J_2 = J(x,y+1)\\ &J_3 = J(x-1,y)\\ &J_4 = J(x+1,y)\\ \end{aligned} I0=I(x,y)I1=I(x,y−1)I2=I(x,y+1)I3=I(x−1,y)I4=I(x+1,y)J0=J(x,y)J1=J(x,y−1)J2=J(x,y+1)J3=J(x−1,y)J4=J(x+1,y)
公式中a6可能存在问题, 这个根据代码实现简化后的公式:
a 1 ( x , y ) = − ψ ( x , y − 1 ) + ψ ( x , y ) 2 a 2 ( x , y ) = − ψ ( x , y + 1 ) + ψ ( x , y ) 2 a 3 ( x , y ) = − ψ ( x − 1 , y ) + ψ ( x , y ) 2 a 4 ( x , y ) = − ψ ( x + 1 , y ) + ψ ( x , y ) 2 a 5 ( x , y ) = ϕ ( x , y ) − a 1 ( x , y ) − a 2 ( x , y ) − a 3 ( x , y ) − a 4 ( x , y ) a 6 ( x , y ) = ϕ ( x , y ) I 0 + a 1 ( x , y ) ( I 1 − I 0 ) + a 2 ( x , y ) ( I 2 − I 0 ) + a 3 ( x , y ) ( I 3 − I 0 ) + a 4 ( x , y ) ( I 4 − I 0 ) \begin{aligned} a_1(x, y)=&-\frac{\psi(x, y-1)+\psi(x, y)}{2} \\ a_2(x, y)=&-\frac{\psi(x, y+1)+\psi(x, y)}{2} \\ a_3(x, y)=&-\frac{\psi(x-1, y)+\psi(x, y)}{2} \\ a_4(x, y)=&-\frac{\psi(x+1, y)+\psi(x, y)}{2} \\ a_5(x, y)=&\phi(x, y) - a_1(x, y) - a_2(x, y) - a_3(x, y) - a_4(x, y) \\ \\ a_6(x, y)=& \phi(x, y) I_0 \\ & +a_1(x, y)(I_1 - I_0) \\ & +a_2(x, y)(I_2 - I_0) \\ & +a_3(x, y)(I_3 - I_0) \\ & +a_4(x, y)(I_4 - I_0) \\ \end{aligned} a1(x,y)=a2(x,y)=a3(x,y)=a4(x,y)=a5(x,y)=a6(x,y)=−2ψ(x,y−1)+ψ(x,y)−2ψ(x,y+1)+ψ(x,y)−2ψ(x−1,y)+ψ(x,y)−2ψ(x+1,y)+ψ(x,y)ϕ(x,y)−a1(x,y)−a2(x,y)−a3(x,y)−a4(x,y)ϕ(x,y)I0+a1(x,y)(I1−I0)+a2(x,y)(I2−I0)+a3(x,y)(I3−I0)+a4(x,y)(I4−I0)
公式19简化为:
a 1 ( x , y ) J 1 + a 2 ( x , y ) J 2 + a 3 ( x , y ) J 3 + a 4 ( x , y ) J 4 + a 5 ( x , y ) J 0 = a 6 ( x , y ) (19) \begin{aligned} &a_1(x, y) J_1+a_2(x, y) J_2+a_3(x, y) J_3+a_4(x, y) J_4+a_5(x, y) J_0 =a_6(x, y) \end{aligned} \tag{19} a1(x,y)J1+a2(x,y)J2+a3(x,y)J3+a4(x,y)J4+a5(x,y)J0=a6(x,y)(19)
将J0单独放到方程的一边, 可以得到:
a 5 ( x , y ) J 0 = ϕ ( x , y ) I 0 a 1 ( x , y ) ( I 1 − I 0 ) − a 1 ( x , y ) J 1 a 2 ( x , y ) ( I 2 − I 0 ) − a 2 ( x , y ) J 2 a 3 ( x , y ) ( I 3 − I 0 ) − a 3 ( x , y ) J 3 a 4 ( x , y ) ( I 4 − I 0 ) − a 4 ( x , y ) J 4 = ϕ ( x , y ) I 0 − A 1 − A 2 − A 3 − A 4 \begin{aligned} a_5(x, y) J_0=&\phi(x, y) I_0 \\ & a_1(x, y)(I_1 - I_0) - a_1(x, y) J_1\\ & a_2(x, y)(I_2 - I_0) - a_2(x, y) J_2 \\ & a_3(x, y)(I_3 - I_0) - a_3(x, y) J_3\\ & a_4(x, y)(I_4 - I_0) - a_4(x, y) J_4\\ & = \phi(x, y) I_0 - A_1- A_2 - A_3 - A_4 \end{aligned} a5(x,y)J0=ϕ(x,y)I0a1(x,y)(I1−I0)−a1(x,y)J1a2(x,y)(I2−I0)−a2(x,y)J2a3(x,y)(I3−I0)−a3(x,y)J3a4(x,y)(I4−I0)−a4(x,y)J4=ϕ(x,y)I0−A1−A2−A3−A4
A 1 = a 1 ( x , y ) ( J 1 − I 1 + I 0 ) A 2 = a 2 ( x , y ) ( J 2 − I 2 + I 0 ) A 3 = a 3 ( x , y ) ( J 3 − I 3 + I 0 ) A 4 = a 4 ( x , y ) ( J 4 − I 4 + I 0 ) A_1 = a_1(x, y)(J_1 - I_1 + I_0) \\ A_2 = a_2(x, y)(J_2 - I_2 + I_0) \\ A_3 = a_3(x, y)(J_3 - I_3 + I_0) \\ A_4 = a_4(x, y)(J_4 - I_4 + I_0) A1=a1(x,y)(J1−I1+I0)A2=a2(x,y)(J2−I2+I0)A3=a3(x,y)(J3−I3+I0)A4=a4(x,y)(J4−I4+I0)
在公式2边除以a5, 可以得到公式20, 即为最后的图像
J 0 = ϕ ( x , y ) I 0 − A 1 − A 2 − A 3 − A 4 a 5 ( x , y ) (20) J_0=\frac{\phi(x, y) I_0 - A_1- A_2 - A_3 - A_4}{a_5(x, y)} \tag{20} J0=a5(x,y)ϕ(x,y)I0−A1−A2−A3−A4(20)
最后, 代码实现时, 对结果进行了加权, 即:
J 0 k + 1 = ϕ ( x , y ) I 0 k − A 1 k − A 2 k − A 3 k − A 4 k a 5 ( x , y ) ∗ ( 1 − ρ ) + J 0 k ∗ ρ (20) J_0^{k+1}= \frac{\phi(x, y) I_0^{k} - A_1^{k}- A_2^{k} - A_3^{k} - A_4^{k}}{a_5(x, y)} * (1 - \rho) + J_0^{k} * \rho \tag{20} J0k+1=a5(x,y)ϕ(x,y)I0k−A1k−A2k−A3k−A4k∗(1−ρ)+J0k∗ρ(20)
3-算法效果
文中给出的算法结果如下:


![[附源码]计算机毕业设计基于springboot的云网盘设计](https://img-blog.csdnimg.cn/dfa876eb43274eb99aeacdf0493ae889.png)
![[Power Query] 日期和时间处理](https://img-blog.csdnimg.cn/e32e5f205503482ebb264c2715548aa1.png)

![[附源码]Python计算机毕业设计Django考试系统](https://img-blog.csdnimg.cn/a37ed9a3197a4395b6724029aa19f0d6.png)