C++算法：排序

排序之一（插入、冒泡、快速排序）
排序之二（归并、希尔、选择排序）

文章目录

C++算法：排序
二、比较排序算法实现
- 4、归并排序
- 5、希尔排序
- 5、选择排序
原创文章，未经许可，严禁转载

本文续：C++算法：排序之一（插入、冒泡、快速排序）

二、比较排序算法实现

4、归并排序

归并排序和前面介绍的三种排序方法不同，这是一个以空间换时间的排序法。归并就是将二个或多个已排序的的序列合并成一个，常用的就是二路归并，所以它的空间复杂度很高。

所以归并排序适用于数据量大，并且对稳定性有要求的场景。它也适用于链表排序，可以在O(nlogn)时间内排序。此外，归并排序多用于需要外部排序的场景，比如磁盘文件的情况下比快排好，因为快排很依赖数据的随机存取，而归并是顺序存取，对磁盘这种外存比较友好。
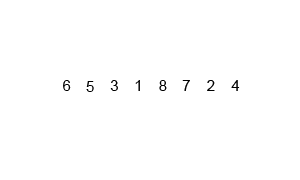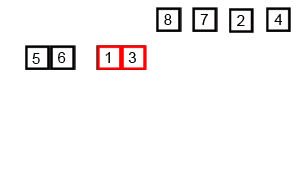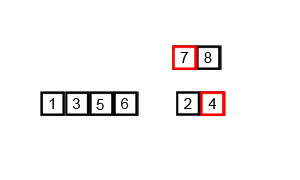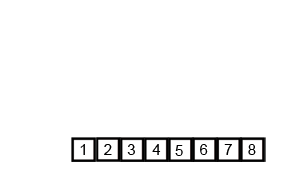
在这里插入图片描述

代码如下（示例）：

#include <iostream>
#include <vector>

using namespace std;

void merge(vector<int> &arr1, vector<int> &arr2, vector<int> &merg){
    int len1 = arr1.size(), len2 = arr2.size();
    int i = 0, j = 0, m = 0;
    while (m < len1 + len2){
        if (i == len1){
            while (j < len2){
                merg[m] = arr2[j];
                j++;
                m++;
            }
            break;
        }
        if (j == len2){
            while (i < len1){
                merg[m] = arr1[i];
                i++;
                m++;
            }
            break;
        }
        if (arr1[i] < arr2[j]){
            merg[m] = arr1[i];
            i++;
            m++;
        } else{
            merg[m] = arr2[j];
            j++;
            m++;
        }
    }
}

void merge_sort(vector<int> &vec){
    int n = vec.size();
    if (n > 1){
        int i = n/2;
        int j = n - n/2;
        vector<int> arr1;
        vector<int> arr2;
        for (int k=0; k<i; k++){
            arr1.push_back(vec[k]);
        }
        for (int k=i; k<j+i; k++){
            arr2.push_back(vec[k]);
        }
        merge_sort(arr1); 
        merge_sort(arr2); 
        merge(arr1, arr2, vec); 
    }
}

int main(){
    vector<int> vec = {6, 5, 3, 1, 8, 7, 2, 4};
    merge_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}

归并排序也是一种遵循分治算法思想的排序方法，它将一个大数组分成两个小数组，对每个小数组进行排序，然后将两个已排序的小数组合并成一个有序的大数组。

在这段代码中，merge_sort 函数是归并排序的主要函数。首先，它检查 vec 的大小是否大于1。如果 vec 的大小小于等于1，则不需要排序，直接返回。否则，将 vec 分成两个部分：arr1 和 arr2。然后，对这两个部分分别调用 merge_sort 函数进行排序。最后，调用 merge 函数将这两个已排序的部分合并成一个有序的大数组。

merge 函数接受三个 vector 类型的引用作为参数：arr1，arr2 和 merg。它将两个已排序的数组 arr1 和 arr2 合并成一个有序的大数组 merg。函数使用三个变量 i，j 和 m 来跟踪三个数组中的位置。当 m < len1 + len2 时（其中 len1 = arr1.size()，len2 = arr2.size()），循环执行以下操作：

如果 i == len1，则将 arr2 中剩余的元素复制到 merg 中，并退出循环。
如果 j == len2，则将 arr1 中剩余的元素复制到 merg 中，并退出循环。
如果 arr1[i] < arr2[j]，则将 arr1[i] 复制到 merg[m] 中，并增加 i 和 m 的值。
否则，将 arr2[j] 复制到 merg[m] 中，并增加 j 和 m 的值。

这里要注意 i、j 是否等于对应长度的检查，应及时用break退出循环，不然可能引起段错误。归并排序虽然代码有点长，但并不难以理解，逻辑是很简单清晰的。

5、希尔排序

希尔是个人名，这是以人名命名的一个排序算法。这是一种很奇特的排序方法，也难怪发明者可以以此留名。它的时间复杂度在比较排序中是较好的，还是就地排序，不额外占用空间。可惜不能对链表结构排序。

希尔排序是一种基于插入排序的算法，它比插入排序和选择排序要快得多，并且数组越大，优势越大。它适用于大型的数组。排序的时间复杂度会比O(n^2)好，但没有快速排序算法快O(n(logn))，在中等大小规模数组表现良好，总之不怎么常用。

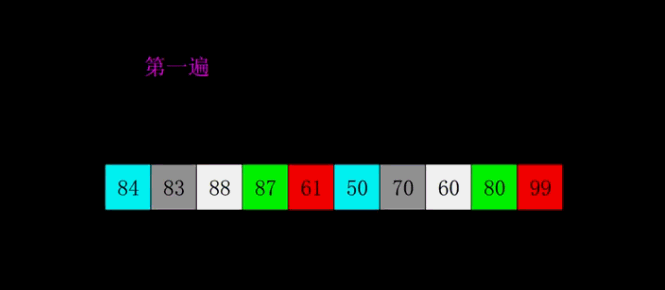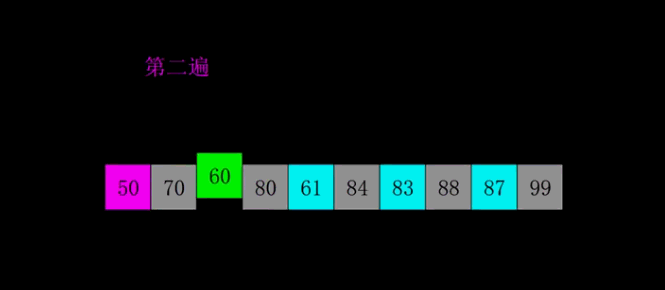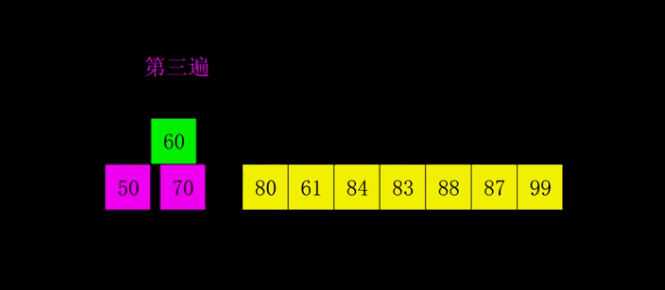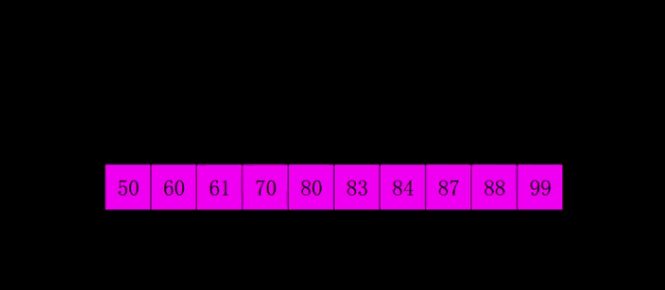
在这里插入图片描述
希尔排序也称为缩小增量排序。它的基本原理是将待排序的数组元素按下标的一定增量分组，分成多个子序列，然后对各个子序列进行直接插入排序算法排序；然后依次缩减增量再进行排序，直到增量为1时，进行最后一次直接插入排序，排序结束。

上图的分组过程表现得不是很直观，下方的过程解释和代码是严格匹配这个分组过程的。

第一遍是分成两个组，gap是增量的意思，总共10个元素，第一遍gap就是5，从0到5这5个元素为1 组，5到10为一组，对这两组进行插入排序。它其实是将两组同样位置的元素比较（第一次是0和5比较），如果1组同位置元素大于2组的，则交换并继续向前以gap差比较。图中同颜色的元素就是比较过程的演示。0:5，1:6，2:7 …
第二遍gap又除以2，gap=2。分成了5组，这样就成了：2组比1组的同位置元素，3组比2组的同位置元素并继续和1组的同位置元素比较，…
第三遍gap就等于1了，那就是一个插入排序过程。

代码如下（示例）：

#include <iostream>
#include <vector>

using namespace std;

void shell_sort(vector<int> &vec){
    int len = vec.size();
    int insert_num = 0;
    int gap = len / 2;      //初始化增量
    while (gap){           //当增量大于等于1时，执行循环
        for (int i = gap; i < len; ++i){       //对每个子序列进行插入排序
            insert_num = vec[i];
            int j = i;
//如果当前元素小于前一个元素，则交换位置, 其实就是插入排序，只是指针设计得特殊
            while (j >= gap && insert_num < vec[j - gap]){   
                vec[j] = vec[j - gap];
                j -= gap;
            }
            vec[j] = insert_num;  //j已经减了gap
        }
        gap = gap / 2; // 减小增量
    }
}

int main(){
    vector<int> vec = {83, 84, 88, 87, 61, 50, 70, 60, 80, 99};
    shell_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}

首先，我们初始化增量 gap 为序列长度的一半。然后，当 gap 大于等于1时，执行循环。在循环中，我们对每个子序列进行插入排序。如果当前元素小于前一个元素，则交换位置。最后，我们减小增量 gap 的值，并重复执行上述操作。当 gap 的值为1时，整个序列就是有序的。在本例中，子序列其实就是插入排序，只是指针设计得特殊，也有使用冒泡排序来进行子序列排序的。

5、选择排序

选择排序是最直观的排序算法了，每次循环拿走最大的元素放在最后位置。循环 n-1 次后，排序就完成了，当然每次取最小元素放前面也是一样的，小学生就能搞明白的算法。
在这里插入图片描述

代码如下（示例）：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

void select_sort(vector<int> &vec){
    int len = vec.size();
    int idx = 0, mini;
    while (idx < len){
        mini = vec[idx];
        for (int i=idx+1; i<len ;++i){
            if (vec[i] < mini){
                mini = vec[i];
            }
        }
        swap(mini, vec[idx]);
        idx++;
    }  
}

int main(){
    vector<int> vec = {2,3,4,5,15,19,26,27,36,38,44,46,47,48,50};
    select_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}