在现实生活中，TopK算法是非常常见的一种应用，你可能已经在电商平台上使用它来搜索最畅销的商品或者在音乐应用中使用它来发现最受欢迎的歌曲。那么，让我们深入了解TopK算法的原理和实现吧！

TopK是什么

• TopK算法是一种常见的统计算法，即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。我们经常需要找出最大的十个销售额最高的商品、最受欢迎的音乐等。这时候TopK算法就非常实用，它可以帮助我们快速地找出所需数据，而不用遍历整个数组。TopK算法是一种非常高效的算法，如使用堆排序思想实现 - TopK时间复杂度为O(nlogk)，n是数据的个数，k是需要查询的数据个数。

---

TopK算法的实现

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能 数据都不能一下子全部加载到内存中)，排序的效率就会变得非常低，甚至无法完成。为了解决这个问题，可以使用一些专门的技术。下面介绍一种处理大数据量Top-K问题的常见方法.

• 基于比较的排序方法可以用来解决TopK问题，其中最著名的算法是堆排序。堆排序使用堆来维护前K个元素，堆的大小为K。基本思路如下：

1. 用数据集合中前K个元素来建堆

• 前k个最大的元素，则建小堆
• 前k个最小的元素，则建大堆

2. 用剩余的N-K个元素依次与堆顶元素来比较，（如取前k个最大）如果比堆顶的数据大，就替换他进堆. (覆盖堆顶值，向下调整)

3. 将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

• 总的来说就是 开辟一段较小的内存空间，先将数据前K个值放入其中，然后用后续的数据逐个与堆顶数据进行比较，如果大于堆顶数据，则将其插入堆中并调整堆，这样最终堆中保留的就是前K个最大的数。

图析

1. 用数据中前K个元素来建堆，假设k是5,把数据前5个建成堆，这个小堆用于存储当前最大的k个元素。
   
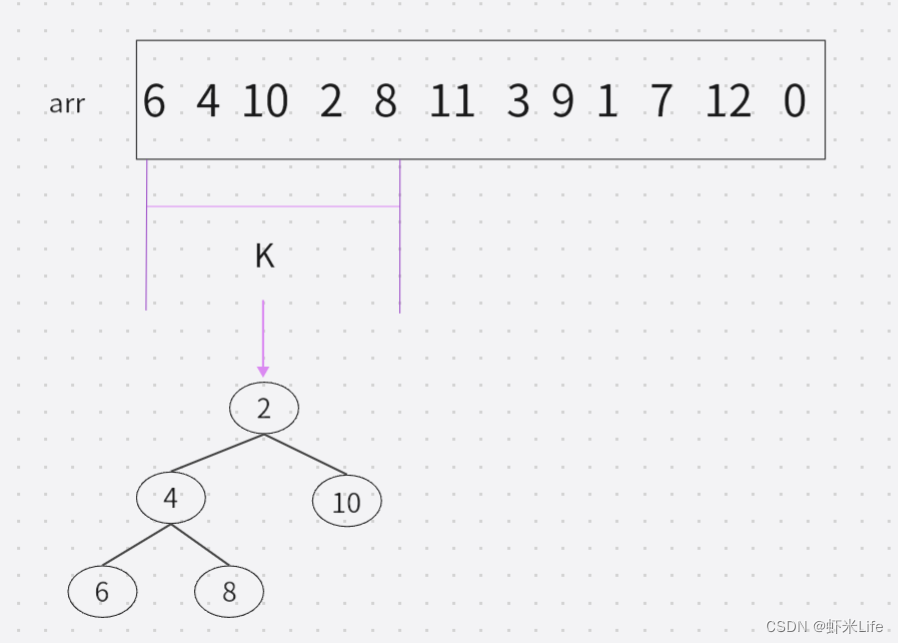
2. 用剩余的N-K个元素依次与堆顶元素来比较,因为堆顶元素是该堆最小值，如比堆顶元素大，就替换他进堆. (覆盖堆顶值，向下调整).
   
   
   
   
   
   

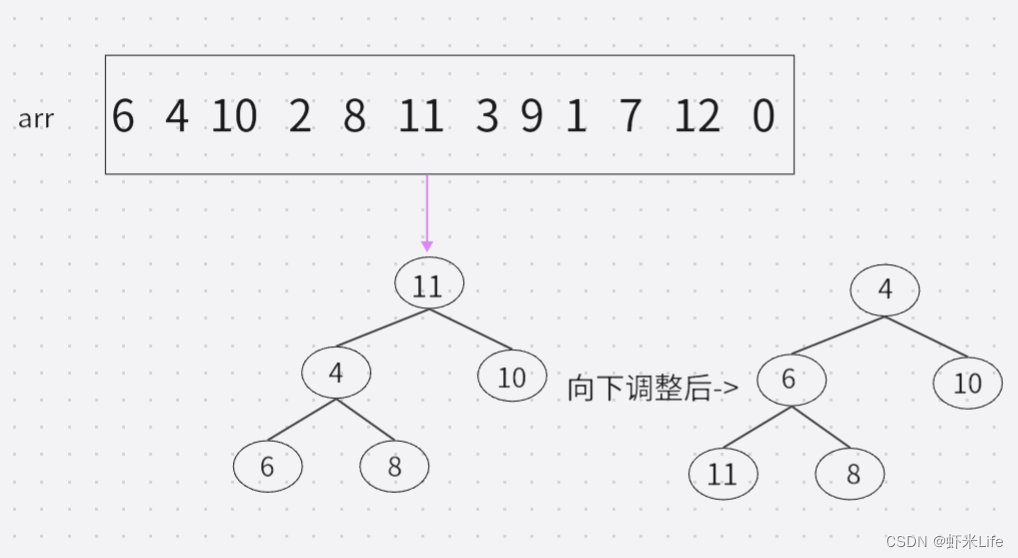
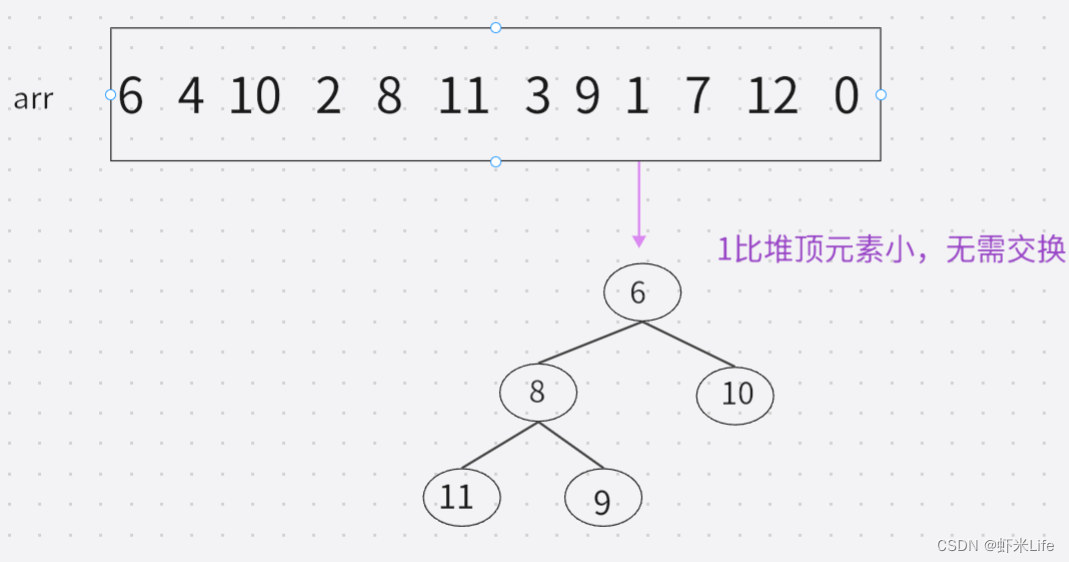
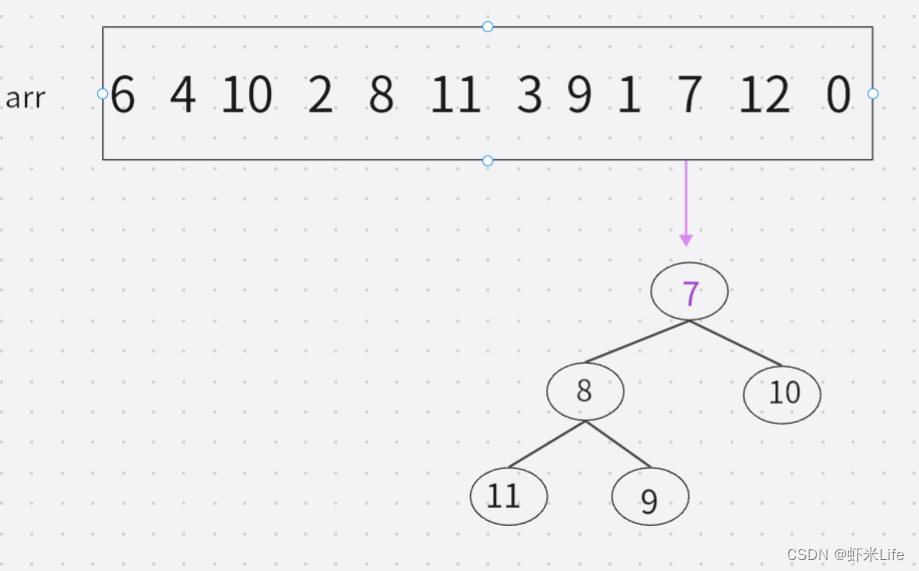
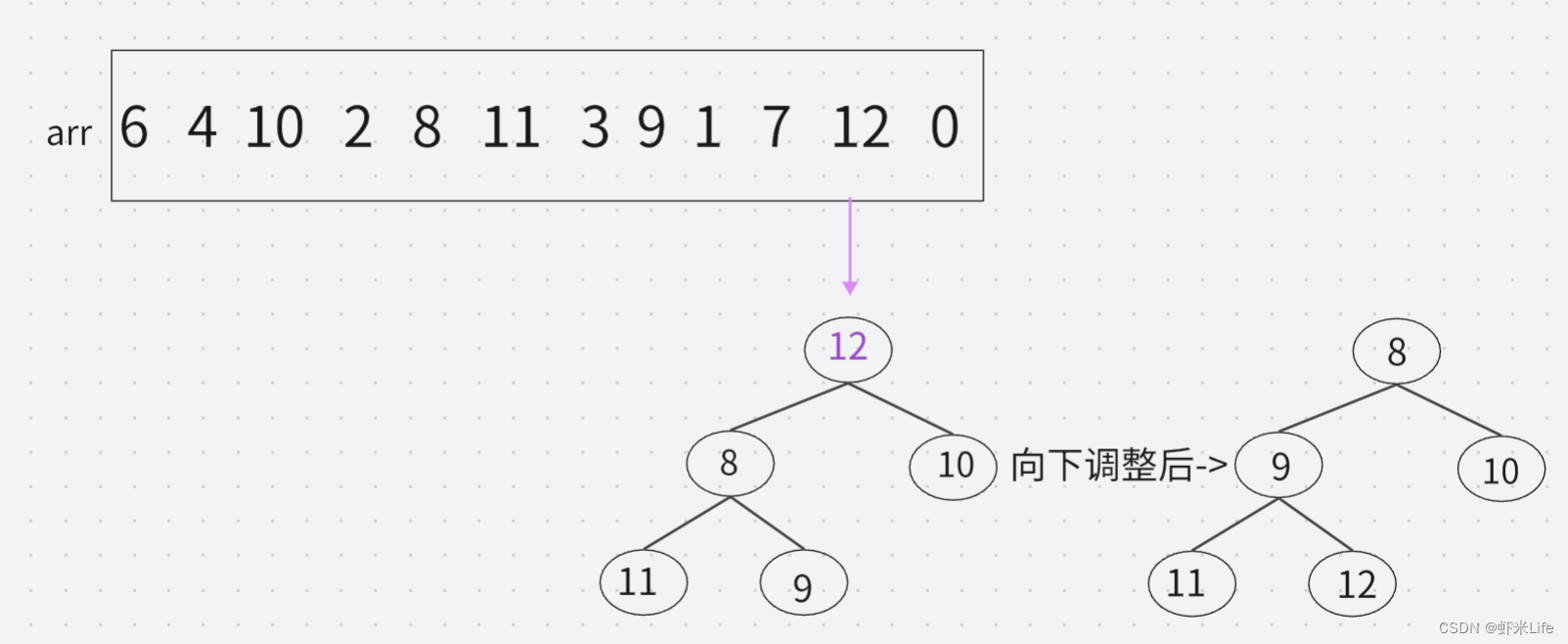
• 依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最大的元素。

代码实现，详细步骤已写注释

void AdjustDown(int* a, int parent, int sz)
{
    int child = parent * 2 + 1;  // 找到父节点的左孩子
    while (child < sz)  // 当左孩子在sz范围内时
    {
        if (child + 1 < sz && a[child] > a[child + 1])  // 如果左孩子比右孩子大
        {
            child++;  // 则将child指向右孩子
        }
        if (a[parent] > a[child])  // 如果父节点比最小的孩子大
        {
            int tmp = a[parent];
            a[parent] = a[child];
            a[child] = tmp;  // 则交换父节点和孩子节点的值
        }
        else  // 如果父节点比最小的孩子小则堆已经建立完成，退出循环
        {
            break;
        }
        parent = child;  // 否则，继续向下调整
        child = parent * 2 + 1;
    }
}

void PrintTopK(int* a, int n, int k)
{
    // 1. 建堆--用a中前k个元素建堆
    for (int i = (k - 1 - 1) / 2; i >= 0; i--)  // 从数组总长度的一半-1开始，向下调整每一个非叶节点
    {
        AdjustDown(a, i, k);  // 将当前节点向下调整
    }

    // 2. 将剩余n-k个元素依次与堆顶元素比较，如果大于堆顶，则替换堆顶，并向下调整
    for (int i = k; i < n; i++)
    {
        if (a[i] > a[0])  // 如果第i个元素比堆顶元素大
        {
            a[0] = a[i];  // 则将堆顶元素替换为第i个元素
            AdjustDown(a, 0, k);  // 向下调整堆顶元素
        }
    }

    // 打印前k个元素
    for (int i = 0; i < k; i++)
    {
        printf("%d ", a[i]);
    }
}

void TestTopk()
{
    int arr[] = { 6,4,10,2,8,11,3,9,1,7,12,0 };
    int sz = sizeof(arr) / sizeof(*arr);
    PrintTopK(arr, sz, 5);
}

输出结果: 8 9 10 11 12

我们换一个大一点的数据来测试一下.

void AdjustDown(int* a, int parent, int sz)
{
    int child = parent * 2 + 1;  // 找到父节点的左孩子
    while (child < sz)  // 当左孩子在sz范围内时
    {
        if (child + 1 < sz && a[child] > a[child + 1])  // 如果左孩子比右孩子大
        {
            child++;  // 则将child指向右孩子
        }
        if (a[parent] > a[child])  // 如果父节点比最小的孩子大
        {
            int tmp = a[parent];
            a[parent] = a[child];
            a[child] = tmp;  // 则交换父节点和孩子节点的值
        }
        else  // 如果父节点比最小的孩子小则堆已经建立完成，退出循环
        {
            break;
        }
        parent = child;  // 否则，继续向下调整
        child = parent * 2 + 1;
    }
}

// 打印前k个最大的元素
void PrintTopK(int* a, int n, int k)
{
    // 1. 建堆--用a中前k个元素建堆
    for (int i = (k - 1 - 1) / 2; i >= 0; i--)  // 从数组总长度的一半-1开始，向下调整每一个非叶节点
    {
        AdjustDown(a, i, k);  // 将当前节点向下调整
    }

    // 2. 将剩余n-k个元素依次与堆顶元素比较，如果大于堆顶，则替换堆顶，并向下调整
    for (int i = k; i < n; i++)
    {
        if (a[i] > a[0])  // 如果第i个元素比堆顶元素大
        {
            a[0] = a[i];  // 则将堆顶元素替换为第i个元素
            AdjustDown(a, 0, k);  // 向下调整堆顶元素
        }
    }

    // 3. 打印前k个元素
    for (int i = 0; i < k; i++)
    {
        printf("%d ", a[i]);
    }
}

// 测试函数
void TestTopk()
{
    int n = 10000;
    int* a = (int*)malloc(sizeof(int) * n);
    srand(time(0));

    // 生成数组
    for (size_t i = 0; i < n; ++i)
    {
        a[i] = rand() % 1000000;
    }

    // 修改一些元素，这些元素就是最大的.
    a[5] = 1000000 + 1;
    a[1231] = 1000000 + 2;
    a[531] = 1000000 + 3;
    a[5121] = 1000000 + 4;
    a[115] = 1000000 + 5;
    a[2335] = 1000000 + 6;
    a[9999] = 1000000 + 7;
    a[76] = 1000000 + 8;
    a[423] = 1000000 + 9;
    a[3144] = 1000000 + 10;

    // 打印前10个最大的元素
    PrintTopK(a, n, 10);
}

输出结果: 1000001 1000002 1000003 1000004 1000006 1000010 1000007 1000008 1000005 1000009

---

总结

堆排序是最常用的实作TopK算法的方案之一，时间复杂度为O(nlogk)，n是元素总个数，k为需要找到的元素个数。TopK算法可应用于海量数据处理，如专业前10名、世界500强、富豪榜、热点事件分析等领域。总之，TopK算法通常应用于需要在大规模数据中查找最大或最小的K个元素的场景，而堆排序是实现这类算法主要的手段之一，其时间复杂度为O(nlogk)。