前言
在数据结构中,排序是非常重要的内容,也是未来面试和笔试的重点。
本文代码是Java
目录
前言
一、插入排序
(一)直接插入排序
(二)希尔排序
二、选择排序
(一)选择排序
(二)堆排序
三、交换排序
(一)冒泡排序
(二)快速排序
四、归并排序
(一)归并排序
五、计数排序
六、其他排序
结语
一、插入排序
(一)直接插入排序
将一条记录插入到已排好的有序表中,从而得到一个新的、记录数量增1的有序表。
适用于顺序表、链表
排序过程如下:
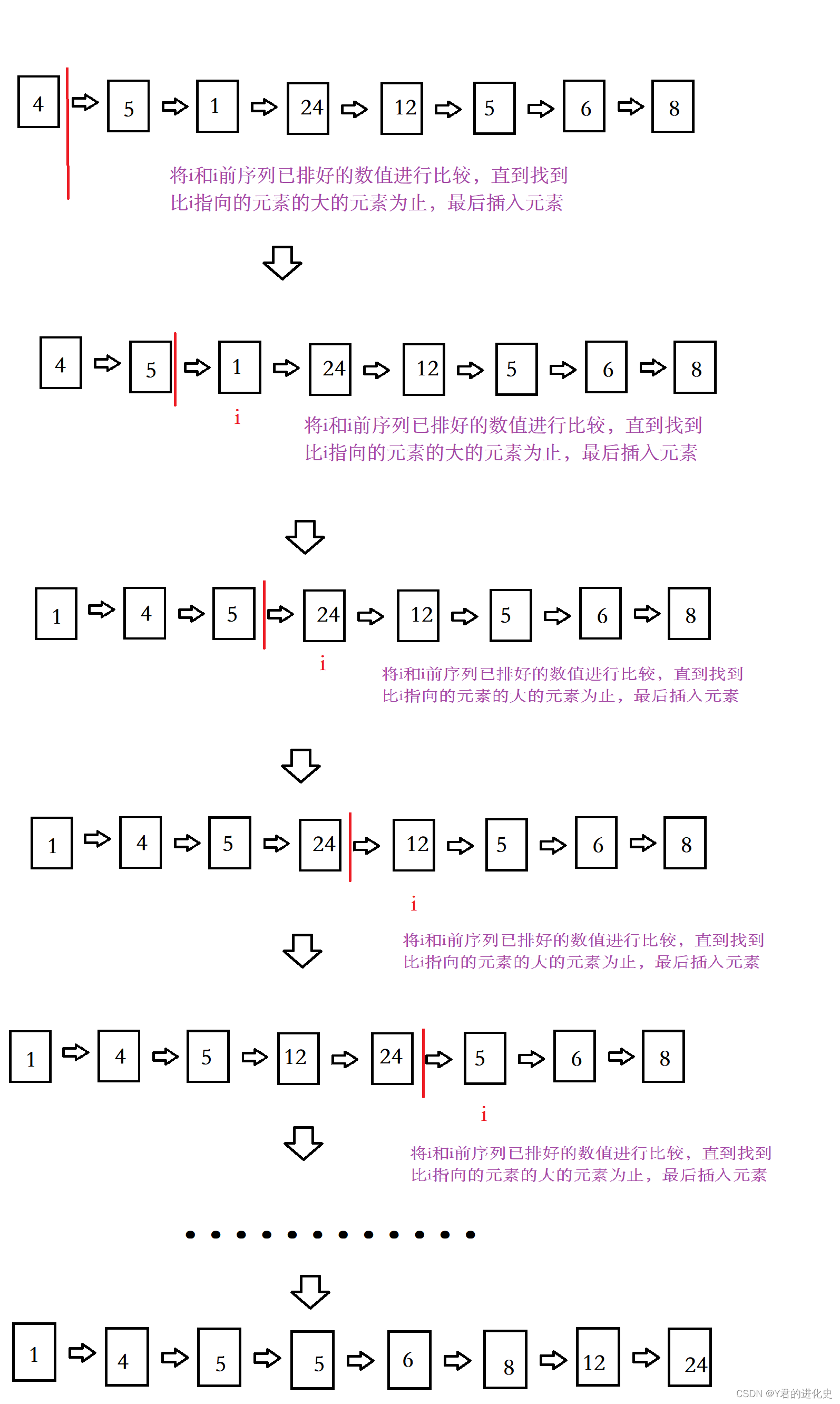
代码:
public static void InlineSort(int[] arr){
for (int i = 1; i < arr.length; i++) {
if(arr[i] < arr[i-1]){
int tmp = arr[i];
int j = i-1;
for (; j >= 0; j--) {
if(arr[j]>tmp){
arr[j+1] = arr[j];
}else{
break;
}
}
arr[j+1] = tmp;
}
}
}时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:稳定
(二)希尔排序
仅适用于顺序表,不适用于链表
记录按下标的一定增量分组,对每组使用直接插入排序算法排序
排序过程如下:
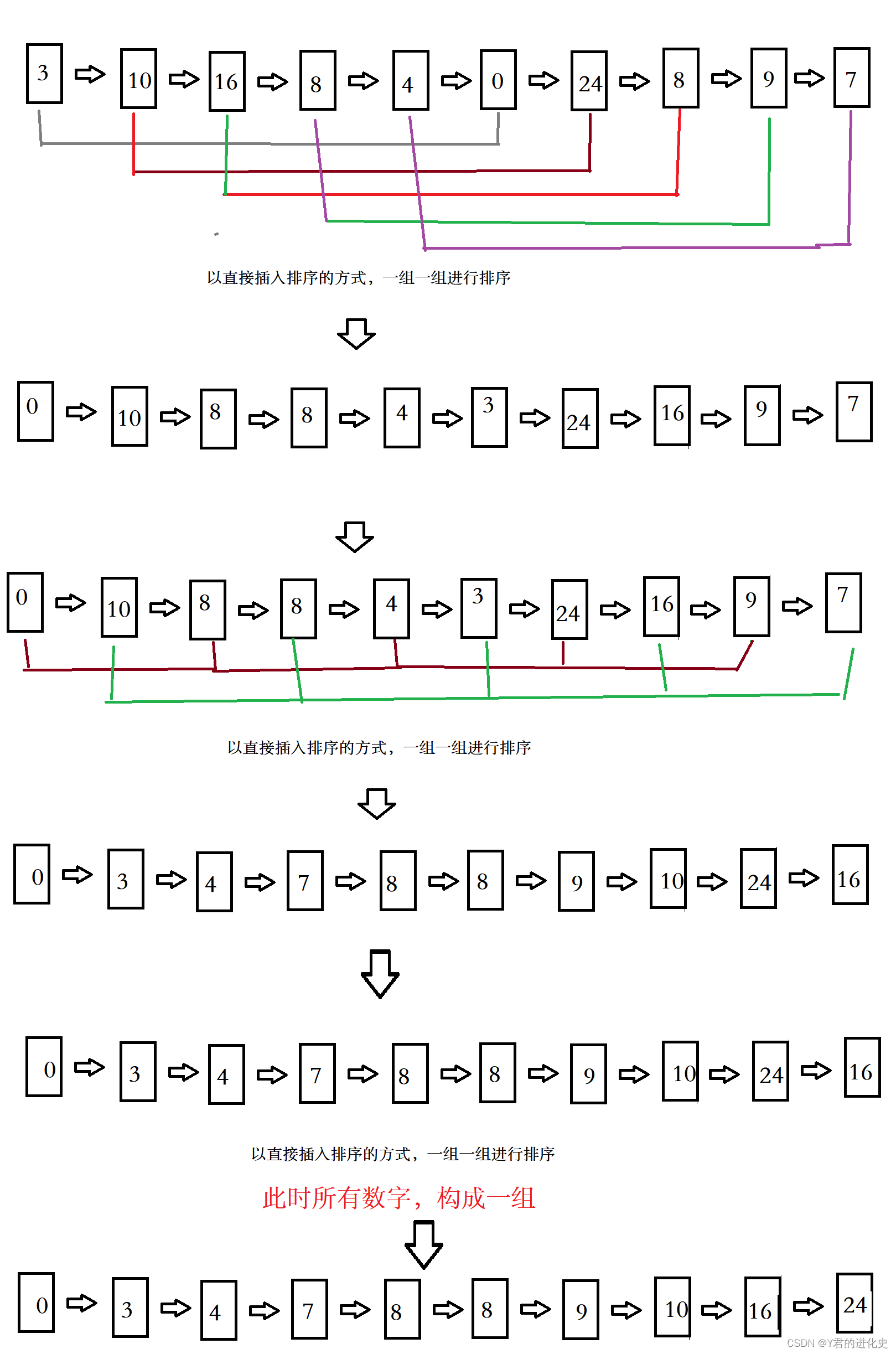
代码:
public static void shellSort(int[] arr){
int len = arr.length;
int d = len/2;//组数,数据之间的间距
while(d >= 1){
for(int i = 0; i < d; i++){
for (int j = i+d; j < len; j+=d) {
int tmp = arr[j];
int k = j-d;
for (; k >= 0; k-=d) {
if(tmp < arr[k]){
arr[k+d] = arr[k];
}else{
break;
}
}
arr[k+d] = tmp;
}
}
d /= 2;
}
}时间复杂度:O(n^1.3)
空间复杂度:O(1)
稳定性:不稳定
二、选择排序
(一)选择排序
在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
顺序表和链表都适用
排序过程:

代码:
public static void selectSort(int[] arr){
int left = 0;
int right = arr.length-1;
while(left < right){
int min = left;
int max = right;
for (int i = left; i <= right; i++) {
if(arr[i] < arr[min]){
min = i;
}
if(arr[i] > arr[max]){
max = i;
}
}
//交换
swap(arr,min,left);
if(left == max){
max = min;
}
swap(arr,max,right);
left++;
right--;
}
}
//交换
public static void swap(int[] arr, int s1, int s2) {
int tmp = arr[s1];
arr[s1] = arr[s2];
arr[s2] = tmp;
}时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定
该排序与数据是否有序无关
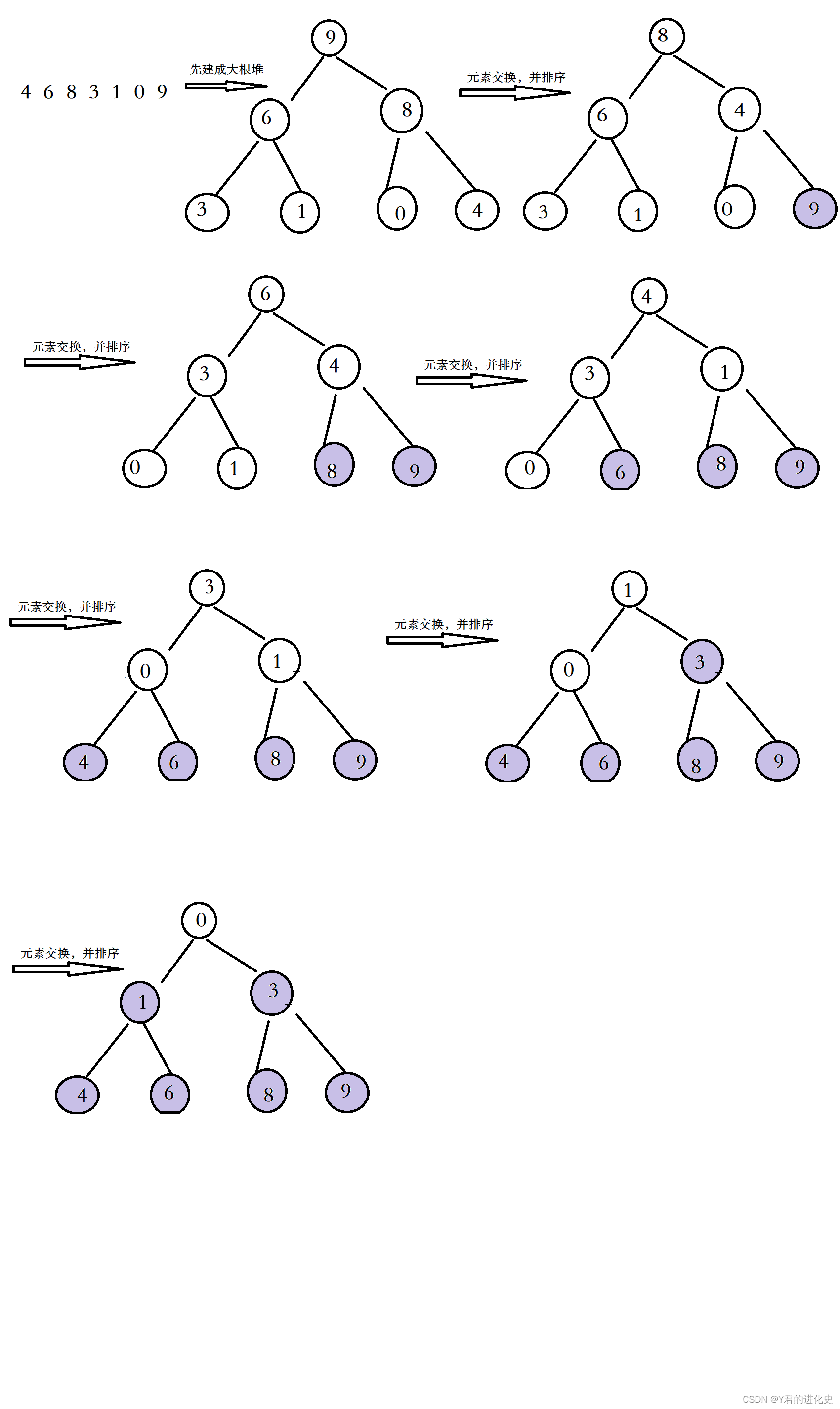
(二)堆排序
建立大根堆 -> 把堆顶与最末尾元素交换,直到建立有序的小根堆
排序过程:
 代码:
代码:
public static void heapSort(int[] arr){
//使arr成为大根堆
int len = arr.length;
for (int i = (len-1-1)/2; i >= 0; i--) {
shiftDown(arr, i, len-1);
}
while(len > 0){
//将堆顶与堆末尾交换
swap(arr,0,len-1);
len--;
shiftDown(arr,0,len-1);
}
}
//向下调整
public static void shiftDown(int[] arr, int parent, int k){
int child = parent*2+1;
while(child <= k){
if(child+1<=k && arr[child+1]>arr[child]){
child++;
}
if(arr[child] > arr[parent]){
swap(arr,parent,child);
parent = child;
child = parent*2+1;
}else{
break;
}
}
}
//交换
public static void swap(int[] arr, int s1, int s2){
int tmp = arr[s1];
arr[s1] = arr[s2];
arr[s2] = tmp;
}时间复杂度:O(n*logn)
空间复杂度:O(1)
稳定性:不稳定
该排序与数据是否有序无关
三、交换排序
(一)冒泡排序
比较相邻的元素。如果第一个比第二个大,就交换他们两个
顺序表和链表都适用
排序过程:

代码:
public static void bubbleSort(int[] arr){
int len = arr.length;
for (int i = 0; i < len-1; i++) {
boolean ret = true;
for (int j = 0; j < len-i-1; j++) {
if(arr[j] > arr[j+1]){
swap(arr, j, j+1);
ret = false;
}
}
if(ret == true){
break;
}
}
}
public static void swap(int[] arr, int s1, int s2){
int tmp = arr[s1];
arr[s1] = arr[s2];
arr[s2] = tmp;
}时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:稳定
该排序与数据是否有序无关
(二)快速排序
本文讲解挖坑法
顺序表和链表都适用
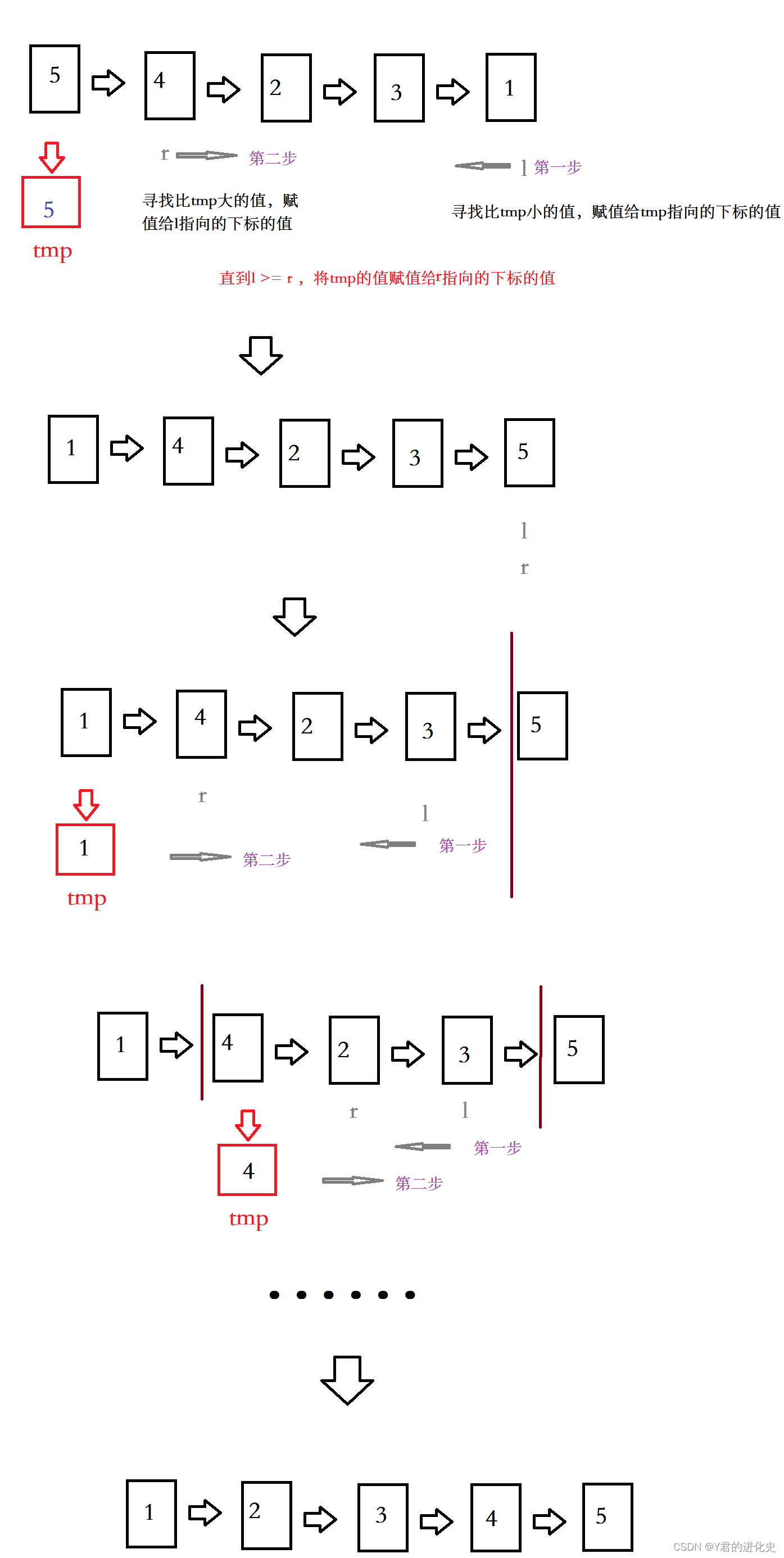
- 以第一个元素为基准,存储在tmp当中,设置l和r两个下标,寻找比tmp小/大的元素,
- 先和tmp交换,再互相交换,直到r和l相等或者r小于l,tmp存储的数值赋值给r指向的下标的位置
- 此时r指向的下标位置把该数据分为两部分,再把这两部分按照上面的步骤进行排序,直到每一个部分只有一个元素或零个元素为止
代码:
public static void quickSort(int[] arr){
quickSortFunc2(arr,0,arr.length-1);
}
//基准 左右不断递归
public static void quickSortFunc2(int[] arr, int left, int right){
//出递归条件
if(left >= right) return;
//优化 当left right中间数字较少时,进行直插
if(right-left+1 <= 7){
insertSort(arr,left,right);
return;
}
//基准下标
int index = quickSortFunc1(arr,left,right);
quickSortFunc2(arr,left,index-1);
quickSortFunc2(arr,index+1,right);
}
//直插
public static void insertSort(int[] arr,int left1, int right1){
for (int i = left1+1; i <= right1; i++) {
int tmp = arr[i];
//最左边下标
int left = 0;
//最右边下标
int right = i-1;
while(left <= right){
int mid = (left+right)/2;
if(tmp < arr[mid]){
right = mid-1;
}else{
left = mid+1;
}
}
for (int j = i-1; j >= right+1; j--) {
arr[j+1] = arr[j];
}
arr[right+1] = tmp;
}
}
//找基准,划分基准左右
public static int quickSortFunc1(int[] arr, int left, int right){
int mid = (left+right)/2;
int index = mid;
if(arr[left] < arr[right]){
if(arr[mid] < arr[left]){
index = left;
}else if(arr[mid] > arr[right]){
index = right;
}
}else{
if(arr[mid] < arr[right]){
index = right;
}else if(arr[mid] > arr[left]){
index = left;
}
}
swap(arr,index,left);
int tmp = arr[left];
while (left < right){
while(left < right && arr[right] >= tmp){
right--;
}
arr[left] = arr[right];
while(left < right && arr[left] <= tmp){
left++;
}
arr[right] = arr[left];
}
arr[left] = tmp;
return left;
}
//交换
public static void swap(int[] arr, int s1, int s2){
int tmp = arr[s1];
arr[s1] = arr[s2];
arr[s2] = tmp;
}时间复杂度:O(n^logn)
空间复杂度:O(log n)
稳定性:不稳定
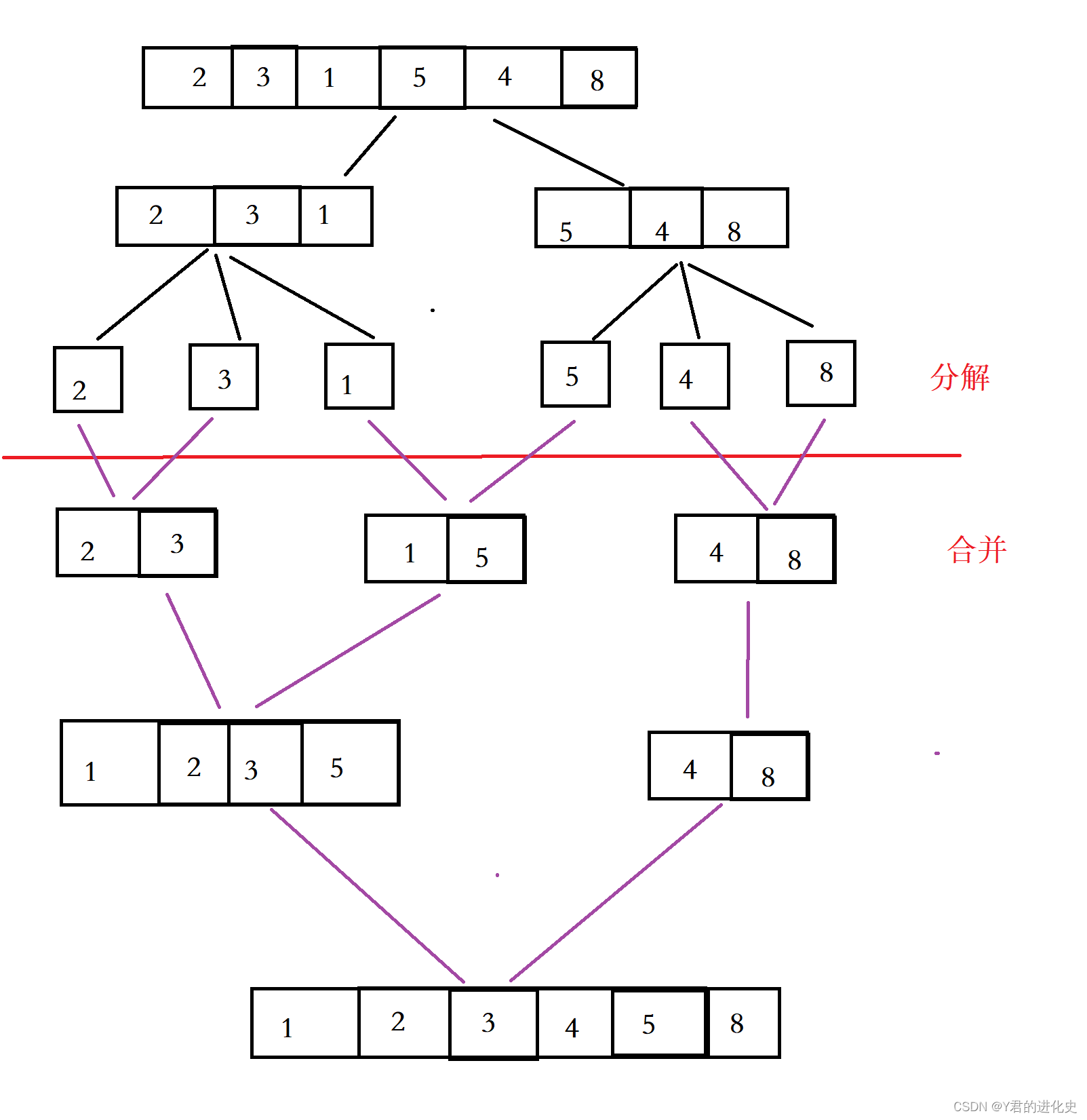
四、归并排序
(一)归并排序
代码:
public static void mergeSort(int[] arr){
mergeSortFunc1(arr,0,arr.length-1);
}
//合并
public static void mergeSortFunc1(int[] arr, int left,int right){
if(left>=right) return;
int mid = (right+left)/2;
mergeSortFunc1(arr,left,mid);
mergeSortFunc1(arr,mid+1,right);
mergeSortFunc2(arr,left,mid,right);
}
//插入
public static void mergeSortFunc2(int[] arr,int left, int mid, int right){
int[] arr1 = new int[right-left+1];
int i = 0;
int tmp =left;
int left2 = mid+1;
while(left<=mid && left2<=right){
if(arr[left] < arr[left2]){
arr1[i++] = arr[left++];
}else{
arr1[i++] = arr[left2++];
}
}
while(left<=mid){
arr1[i++] = arr[left++];
}
while(left2<=right){
arr1[i++] = arr[left2++];
}
for (int j = 0; j < i; j++) {
arr[tmp+j] = arr1[j];
}
}时间复杂度:O(n*logn)
空间复杂度:O(n)
稳定性:稳定
该排序与数据是否有序无关
五、计数排序
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列
代码:
public static void CountSort(int[] arr){
int min = arr[0];
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if(arr[i] < min){
min=arr[i];
}
if(arr[i] > max){
max = arr[i];
}
}
int[] arr1 = new int[max-min+1];
for (int i = 0; i < arr.length; i++) {
arr1[arr[i]-min]++;
}
int k = 0;
for (int i = 0; i < arr1.length; i++) {
while(arr1[i]-- > 0){
arr[k++] = min+i;
}
}
}六、其他排序
基数排序(无比较排序):
创建十个的队列(依次代表 0 1 2 3 4 5 6 7 8 9),从所有数据的最高位开始入队列再出队列,直到根据个位数的数据完成出队列时,总数据完成排序。
桶排序:
创建对应的桶,桶内排序。
结语
本文排序都是递归写法,如果对非递归写法有兴趣了解,可以点击Yjun6/DataStructrue: data_structrue (github.com)
排序有很多,期待我们下次再见!
小编能力有限,有问题和疑惑评论区见哦~