1.新年好（dfs+最短路）
信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)
http://ybt.ssoier.cn:8088/statusx.php?runidx=17472125
先两两求一遍最短路，求一个地方到另一个地方的最短路，在枚举5个拜访的顺序
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10,M=2e5+10,INF=0x3f3f3f3f;
int e[M],ne[M],w[M],h[N],idx;
int dist[6][N];
bool st[N];
int id[6];
int n,m;
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void spfa(int start,int dist[])//求从一个起点到其他所有点的最短距离，待会dfs使用是可以直接查表dist【start】【j】
{
memset(dist,0x3f,4*N);
queue<int> q;
dist[start]=0;
q.push(start);
while(q.size())
{
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
if(!st[j])
{
q.push(j);
st[j]=true;
}
}
}
}
}
int dfs(int cnt,int u,int sum)//cnt是目前已经拜访的数量，u表示从哪一个过来的，sum表示目前的总和
{
if(cnt==6)//假如已经拜访了6个了
{
return sum;
}
int res=INF;
for(int i=1;i<6;i++)//枚举需要拜访的五个
if(!st[i])//假如这个亲戚没用拜访过
{
int j=id[i];//看这个亲戚在那个车站
st[i]=true;//标记这个亲戚已经拜访过了
res=min(res, dfs(cnt+1,i,sum+dist[u][j]));//拜访下一个亲戚
st[i]=false;//回溯
}
return res;
}
int main()
{
cin>>n>>m;
id[0]=1;
for(int i=1;i<=5;i++)cin>>id[i];
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
}
for(int i=0;i<6;i++)spfa(id[i],dist[i]);//求以每个为起点的最短路，用spfa
cout<<dfs(1,0,0);//算一下已经有一个点也就是1号点，然后前一个是0，总花费时间为0
}
2.通信线路（二分+最短路）
340. 通信线路 - AcWing题库https://www.acwing.com/problem/content/342/
#include<bits/stdc++.h>
using namespace std;
const int N=1010,M=2e5+10;
int h[N],e[M],ne[M],w[M],idx;
int dist[N];
bool st[N];
deque<int> q;
int n,m,k;
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool check(int mid)
{
memset(st,0,sizeof st);//清空上一层状态
memset(dist,0x3f,sizeof dist);//清空上一层状态
q.push_back(1);
dist[1]=0;
while(q.size())
{
int t=q.front();
q.pop_front();
if(st[t]) continue;//假如已经搜过了
st[t]=true;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
int d=w[i]>mid;//d是假如大于mid就是1，反之就是0，用双端队列广搜
if(dist[j]>dist[t]+d)
{
dist[j]=dist[t]+d;
if(d) q.push_back(j);//假如是1，加到队尾中
else q.push_front(j);//反之加到队头中
}
}
}
return dist[n]<=k;//返回是否有小于等于k个大于mid的
}
int main()
{
cin>>n>>m>>k;
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
}
int l=0,r=1000001;//l是可以等于0的,r假如等于1e6+1,说明无解
while(l<r) //二分的右边界模板
{
int mid=l+r>>1;
if(check(mid))r=mid;//假如是满足的，说明我的花费可以更小
else l=mid+1;//反之花费就更大
}
if(r==1000001)r=-1;
cout<<r;
}3.道路与航线（最短路+拓扑排序+dfs）
342. 道路与航线 - AcWing题库https://www.acwing.com/problem/content/description/344/
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> pii;
const int N=25010,M=150010,INF=0x3f3f3f3f;
int h[N],ne[M],e[M],idx,w[M];
int n,m1,m2,s;
int id[N];//存每个点所在的连通块
vector<int> block[N];//用来存每个连通块的点
int dist[N];
bool st[N];
int bcnt;//用来记录连通块的个书包
int din[N];//标记每个点的入度
queue<int> q;
void add(int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dijkstra(int bid)//bid是当前连通块
{
priority_queue<pii,vector<pii>,greater<pii>> heap;
for(auto ver:block[bid]) heap.push({dist[ver],ver});//把该连通块的所有点都放进堆中
while(heap.size())
{
auto t=heap.top();
heap.pop();
int ver=t.y,distance=t.x;
if(st[ver]) continue;
st[ver]=true;
for(int i=h[ver];~i;i=ne[i])
{
int j=e[i];
if(dist[j]>distance+w[i])//假如可以更新
{
dist[j]=distance+w[i];
if(id[j]==id[ver]) heap.push({dist[j],j});//假如是一个连通块内部的，则放进堆中
}
if(id[j]!=id[ver]&&--din[id[j]]==0) q.push(id[j]);//假如不是一个连通块的，则另一个连通块入度减一，假如减到0了，则放进拓扑队列中
}
}
}
void topsort()
{
memset(dist,0x3f,sizeof dist);//初始化每个点的距离
dist[s]=0;//起点的距离为0
for(int i=1;i<=n;i++)//搜索入度为0的点进行拓扑队列中
if(!din[i])
q.push(i);
while(q.size())
{
int t=q.front();//取出拓扑队头
q.pop();
dijkstra(t);//把该点内部跑一遍djikstra,更新内部点的最短距离
}
}
void dfs(int u,int ver)//u是该点，ver是该连通块
{
block[ver].push_back(u);//把这个点加到该连通块中
id[u]=ver;//标记这个点的连通块是ver
for(int i=h[u];~i;i=ne[i])//枚举这个点相连的点
{
int j=e[i];
if(!id[j]) dfs(j,ver);//假如还还没更新过，也就是没连通块，则放进跟我一起的连通块中
}
}
int main()
{
cin>>n>>m1>>m2>>s;
memset(h,-1,sizeof h);
while(m1--)//道路建两条边
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
}
for(int i=1;i<=n;i++)//搜索那些连通块，也就是哪些道路可以互相到达的
if(!id[i])//假如该点没用在某个连通块中
dfs(i,++bcnt);//搜索这个点，新开一个连通块
while(m2--)//航线建单向边
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
din[id[b]]++;
}
topsort();//进行拓扑排序，因为连通块之间是拓扑图可以用拓扑排序
for(int i=1;i<=n;i++)//输出每个点的距离
{
if(dist[i]>=INF/2) puts("NO PATH");
else cout<<dist[i]<<endl;
}
return 0;
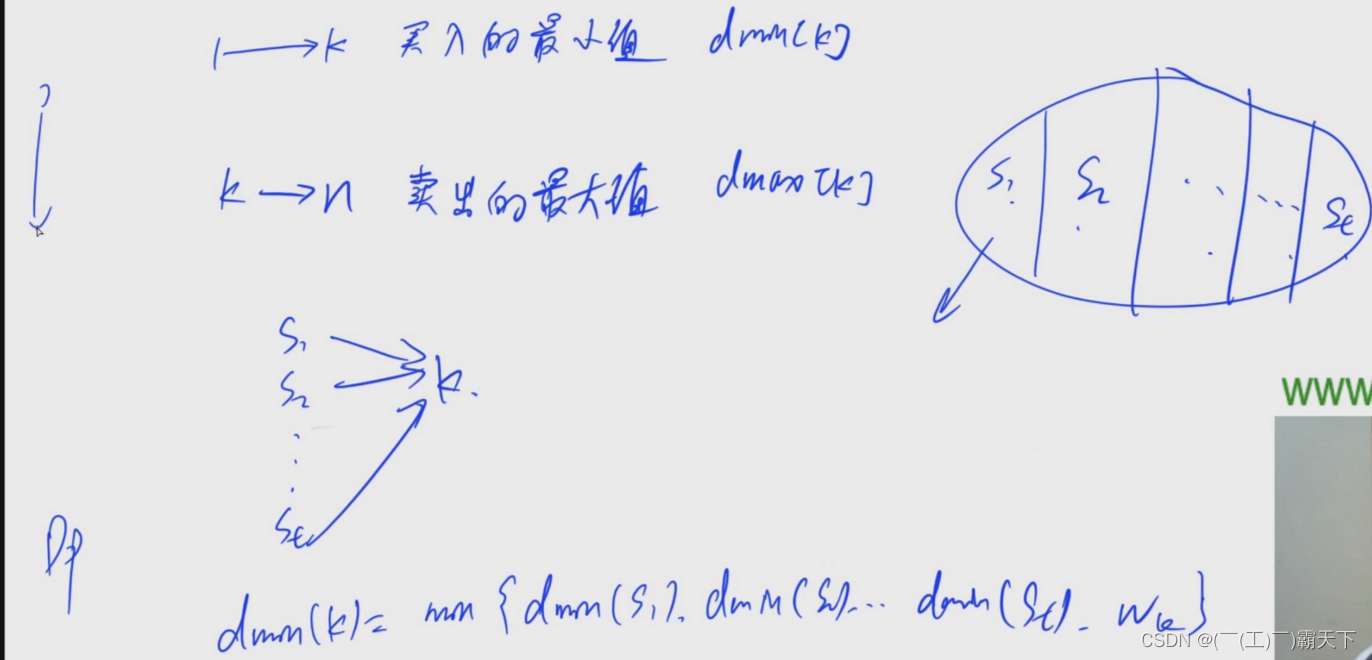
}4.最优贸易（dp+最短路）
341. 最优贸易 - AcWing题库https://www.acwing.com/problem/content/343/
由于可能存在环，所以不能用堆优化dijkstar来做
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=1e6+10;
int hs[N],ne[M],e[M],idx,w[M],ht[N];
int n,m;
int dmin[N],dmax[N];
int q[N];
bool st[N];
void add(int h[],int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void spfa(int h[],int dist[],int type)
{
int hh=0,tt=1;
if(type==0)//假如是求最小值
{
memset(dist,0x3f,sizeof dmin);//初始化为正无穷
dist[1]=w[1];//从1号点开始
q[0]=1;//放进队列中
}
else//假如是求最大值
{
memset(dist,-0x3f,sizeof dmax);//初始化为负无穷
dist[n]=w[n];//从n号点开始
q[0]=n;//把n号点放进队列中
}
while(hh!=tt)
{
int t=q[hh++];
if(hh==N) hh=0;
st[t]=false;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
if(type==0&&dist[j]>min(dist[t],w[j])||type==1&&dist[j]<max(dist[t],w[j]))//假如是两个类型的其中一个且满足最大或者最小
{
if(type==0) dist[j]=min(dist[t],w[j]);//更新类型0
else dist[j]=max(dist[t],w[j]);//更新类型1
if(!st[j])//假如不在队列里则入队
{
q[tt++]=j;
if(tt==N) tt=0;
st[j]=true;
}
}
}
}
}
int main()
{
cin>>n>>m;
memset(hs,-1,sizeof hs);
memset(ht,-1,sizeof ht);
for(int i=1;i<=n;i++) cin>>w[i];
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
add(hs,a,b),add(ht,b,a);//正向与方向加边
if(c==2) add(hs,b,a),add(ht,a,b);
}
spfa(hs,dmin,0);//正向做一遍spfa求前i个的最小值
spfa(ht,dmax,1);//反向做一遍spfa求后i个的最大值
int res=0;
for(int i=1;i<=n;i++) res=max(res,dmax[i]-dmin[i]);//更新一下最大值
cout<<res<<endl;
return 0;
}
