Linear predictions 线性预测

分类

从具有有限离散标签的数据中学习。机器学习中的主导问题

线性分类器

二元分类可以看作是在特征空间中分离类的任务(特征空间）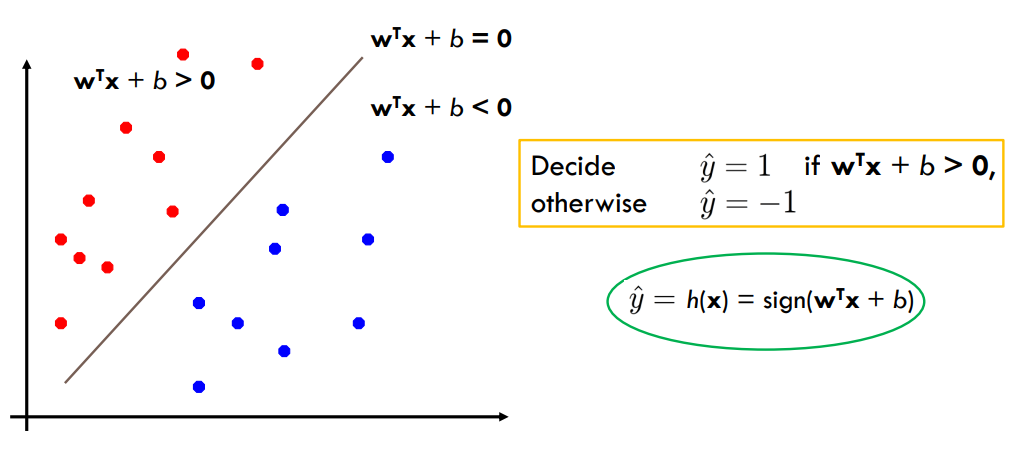

感知机

感知机是一种线性分类模型。它的决策边界是一个超平面，将特征空间分成了两个部分，分别对应于输出为 +1 和 -1 的两个类别。

感知机的线性分类模型可以表示为：

$$f(x)=\text{sign}(\mathbf{w}\cdot \mathbf{x}+b)$$

其中$\mathbf{w}$和$\mathbf{b}$为感知机模型参数，$\mathbf{w}\in {\text{R}}^n$ 是权重或者权值向量，$\mathbf{x}$ 是输入的特征向量，$b\in \text{R}$ 是偏置(bias)，$w\cdot x$ 表示$w$和$x$的内积，$\text{sign}(\cdot )$ 是符号函数。
$$\text{sign}(x)=\{\begin{array}{l}+1,x\ge 0\\ -1,x<0\end{array}$$
感知机的训练目标是找到一个能够将训练集中的正负样本完全分开的超平面，即找到一个合适的权重向量 $\mathbf{w}$ 和偏置项 $b$，使得对于任意训练样本 $({\mathbf{x}}_i,y_i)$，都有
$$y_i(\mathbf{w}\cdot {\mathbf{x}}_i+b)>0$$

这个式子表达了感知机模型的训练目标，即让感知机能够对训练集中的正负样本进行完全分开，使得每个样本都被正确分类。

对于一个训练样本 $({\mathbf{x}}_i,y_i)$，$y_i$ 是其真实的标签，${\mathbf{x}}_i$是其特征向量，$\mathbf{w}$ 是感知机的权重向量，$b$ 是偏置项。根据感知机模型的定义，当 $\mathbf{w}\cdot {\mathbf{x}}_i+b>0$ 时，模型的输出为 +1，否则输出为 -1。

因此，当 $y_i=+1$ 时，要求 $\mathbf{w}\cdot {\mathbf{x}}_i+b>0$，即要求模型将正样本正确分类为 +1。同理，当 $y_i=-1$ 时，要求 $\mathbf{w}\cdot {\mathbf{x}}_i+b<0$，即要求模型将负样本正确分类为 -1。

综合以上两种情况，我们可以将训练目标表达为 $y_i(\mathbf{w}\cdot {\mathbf{x}}_i+b)>0$，即要求每个训练样本都被正确分类，即对于任意训练样本 $({\mathbf{x}}_i,y_i)$，都有 $y_i(\mathbf{w}\cdot {\mathbf{x}}_i+b)>0$。如果存在任意一个训练样本不能被正确分类，那么就需要不断地更新权重向量和偏置项，直到训练集中的所有样本都能被正确分类。

感知机学习策略

1. 数据集线性可分性
2. 在二维平面中，可以用一条直线将+1类和-1类完美分开，那么这个样本空间就是线性可分的。下图中的样本就是线性不可分的，感知机就不能处理这种情况。因此，感知机都基于一个前提：问题空间线性可分

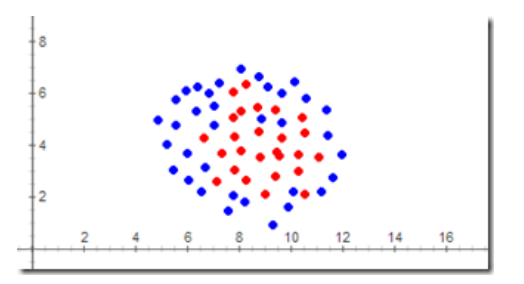
损失函数的选取

1. 损失函数的一个自然选择就是误分类点的总数，要找到决策边界，即分类超平面，使得分类误差最小，可以通过最小化期望的 0/1 损失函数来实现。对于一个样本 $(x,y)$，0/1 损失函数定义为：

   $$L(h(\text{x}),y)=\{\begin{array}{l}0,h(\text{x})=y\\ 1,h(\text{x})\ne y\end{array}$$
   其中，$h(\text{x})$ 是模型预测的输出，$y$ 是样本的真实标签。但是这样的点不是参数$w，b$的连续可导函数，不易优化

2. 损失函数的另一个选择就是误分类点到划分超平面$S(\text{w}\cdot \text{x}+b=0)$的总距离
   

距离的计算

点 $x_0$ 到超平面 $S:w^{T}x+b=0$ 的距离$d$(注: $x_0,w,x$全为N维向量)可以通过以下步骤计算：

1. 设点 $x_0$ 在平面 $S$ 上的投影为 $x_1$，则有 $w^T{x}_1+b=0$
2. -
   

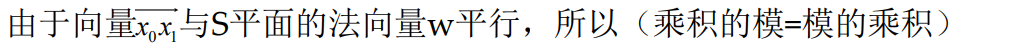
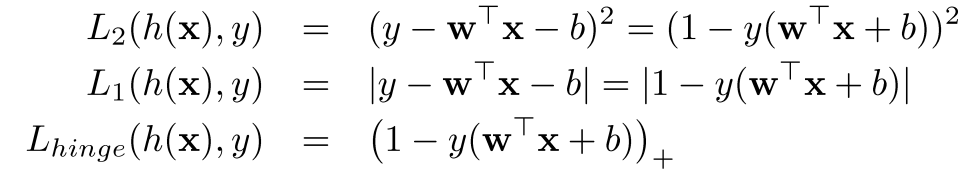
Lhinge（也称为 hinge 损失函数）是一种常用的分类器损失函数，通常用于支持向量机（SVM）和感知机等模型 中。它的形式如下：

L h i n g e ( w , b ; x , y ) = max ⁡ { 0 , 1 − y ( w T x + b ) } L_{hinge}(w,b;x,y) = \max\{0, 1 - y(w^Tx+b)\} Lhinge​(w,b;x,y)=max{0,1−y(wTx+b)}

其中，$w$ 和 $b$ 是模型的参数，$x$ 是输入样本，$y$ 是样本的标签，取值为 $+1$ 或 $-1$，表示正类或负类。$h(x)=\text{sign}(w^{T}x+b)$ 表示模型对样本 $x$ 的预测输出。
当模型对样本 $x$ 的预测结果正确时（即 $y(h(x))>0$），损失函数为 $0$；当模型对样本 $x$ 的预测结果错误时（即 $y(h(x))\le 0$），损失函数为 $1-y(h(x))(w^{T}x+b)$。
这个损失函数的含义是，对于误分类的样本，我们希望让其距离超平面至少为 $1$，即 $y(w^{T}x+b)\ge 1$，如果距离小于 $1$，则损失函数为 $1-y(w^{T}x+b)$，表示分类错误的程度；如果距离大于等于 $1$，则损失函数为 $0$，表示分类正确。
Lhinge 损失函数是一个凸函数，但不是连续可导的，因为在 $y(w^{T}x+b)=1$
时，存在一个“拐点”，导致其导数不连续。因此，在使用梯度下降等优化算法时，需要使用次梯度（subgradient）来代替导数，使得算法可以收敛。同时，Lhinge
损失函数也可以通过一些优化算法（如 SMO 算法）来求解支持向量机模型的最优解。

最小二乘法分类

最小二乘损失函数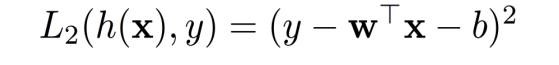
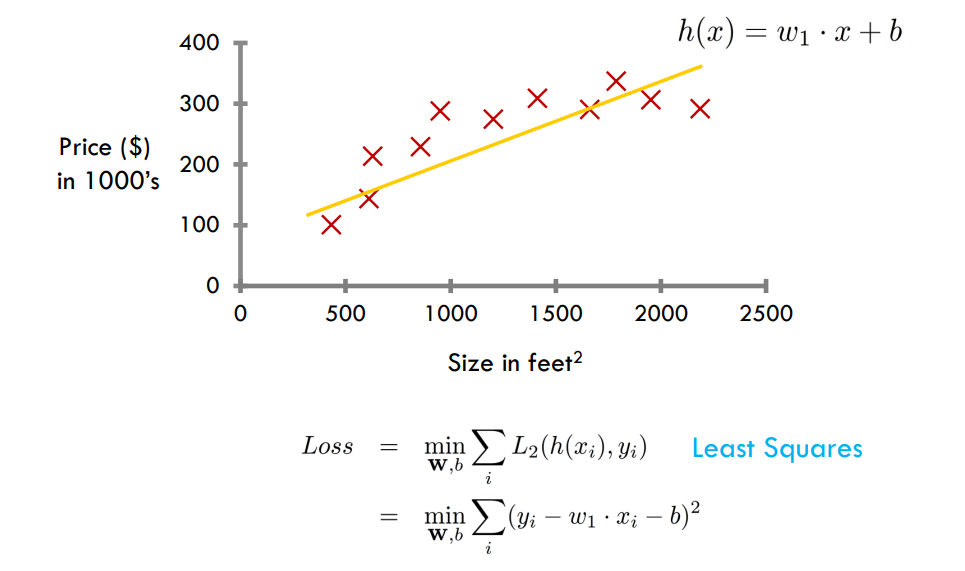
目标：学习分类器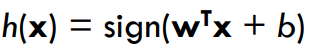以最小化最小二乘损失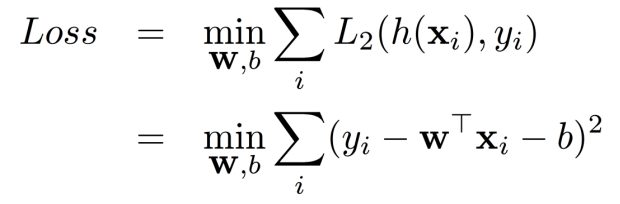

求解最小二乘分类

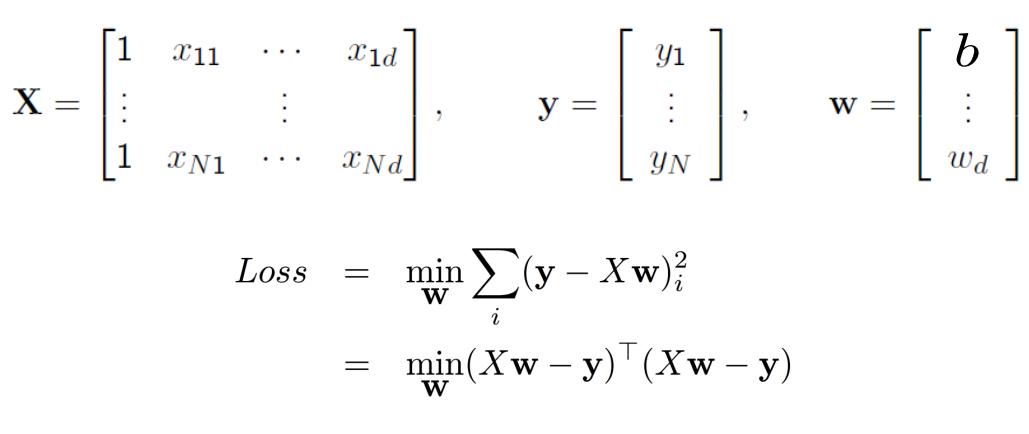
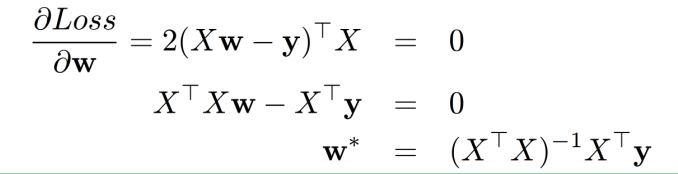
矩阵解法

线性回归定义为：
$$h_{\theta }\left(x_1,x_2,\dots x_{n-1}\right)={\theta }_0+{\theta }_1{x}_1+\dots +{\theta }_{n-1}{x}_{n-1}$$
其中 $\theta$ 为参数。假设现在有 $m$ 个样本，每个样本有 $n-1$ 维特征，将所有样本点代入模型中得：
$$\begin{array}{rl}{h}_1& ={\theta }_0+{\theta }_1{x}_{1,1}+{\theta }_2{x}_{1,2}+\dots +{\theta }_{n-1}{x}_{1,n-1}\\ h_2& ={\theta }_0+{\theta }_1{x}_{2,1}+{\theta }_2{x}_{2,2}+\dots +{\theta }_{n-1}{x}_{2,n-1}\\ & ⋮\\ h_m& ={\theta }_0+{\theta }_1{x}_{m,1}+{\theta }_2{x}_{m,2}+\dots +{\theta }_{n-1}{x}_{m,n-1}\end{array}$$

为方便用矩阵表示，我们令 $x_0=1$，于是上述方程可以用矩阵表示为：$$\mathbf{h}=\mathbf{X}\theta$$
其中，$\mathbf{h}$ 为 $m\times 1$ 的向量，代表模型的理论值，$\theta$ 为 $n\times 1$ 的向量，$\mathbf{X}$ 为 $m\times n$ 维的矩阵，$m$ 代表样本的个数，$n$ 代表样本的特征数。于是目标损失函数用矩阵表示为：
$$J(\theta )=\Vert \mathbf{h}-\mathbf{Y}{\Vert }^2=\Vert \mathbf{X}\theta -\mathbf{Y}{\Vert }^2=(\mathbf{X}\theta -\mathbf{Y}{)}^T(\mathbf{X}\theta -\mathbf{Y})$$
其中 $\mathbf{Y}$ 是样本的输出向量，维度为 $m\times 1$。

根据高数知识我们知道函数取得极值就是导数为0的地方，所以我们只需要对损失函数求导令其等于0就可以解出 $\theta$。矩阵求导属于矩阵微积分的内容，我们先介绍两个用到的公式：
$$\frac{\partial x^{T}a}{\partial x}=\frac{\partial a^{T}x}{\partial x}=a$$
$$\frac{\partial x^{T}Ax}{\partial x}=Ax+A^{T}x$$
如果矩阵 $A$ 是对称的：
$$Ax+A^{T}x=2Ax$$
对目标函数化简：
$$J(\theta )={\theta }^T{X}^{T}X\theta -{\theta }^T{X}^{T}Y-Y^{T}X\theta +Y^{T}Y$$
求导令其等于0：
$$\frac{\partial }{\partial \theta }J(\theta )=2X^{T}X\theta -2X^{T}Y=0$$
解得：
$$\theta ={\left(X^{T}X\right)}^{-1}{X}^{T}Y$$
经过推导我们得到了 $\theta$ 的解析解，现在只要给了数据，我们就可以带入解析解中直接算出 $\theta$。

一般线性分类

基函数（非线性）

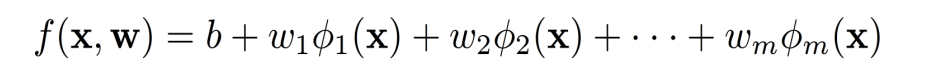
其中$\varphi$为基函数，用于拟合非线性

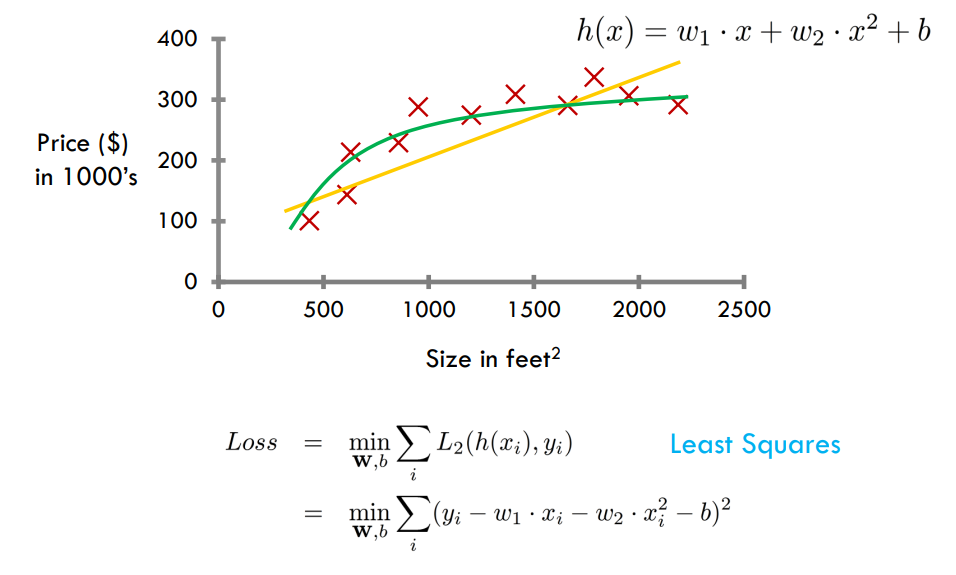
模型复杂性和过度拟合

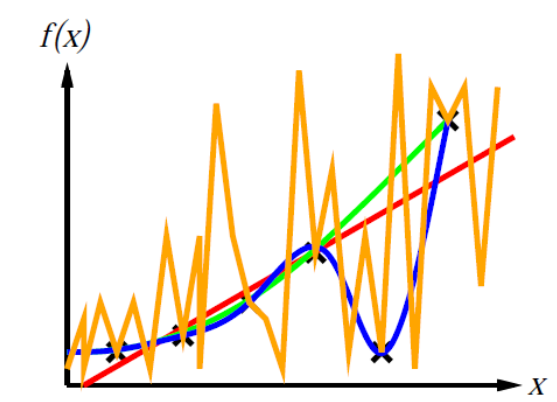
Ockham‘s razor（奥卡姆剃刀原则）: maximize a combination of consistency and simplicity
优先选择与数据一致的最简单的假设

训练误差

训练误差（Training errors），也称为表观误差（Apparent errors），是指在训练数据集上用模型进行训练时所产生的误差。训练误差是模型在学习过程中不可避免的产物，通常我们希望训练误差越小越好，因为模型对训练数据的拟合程度越高，就越可能对未知数据产生良好的预测能力。但是，如果模型过于拟合训练数据，训练误差可能会变得非常小，但是这种模型可能会过度拟合，对于未知数据的预测性能将变得很差。

测试误差

测试误差（Test errors）是指在测试数据集上用模型进行测试时所产生的误差。测试误差用于评估模型的泛化能力，即模型是否具有对未知数据的预测能力。测试误差与训练误差之间的差异通常被称为泛化误差。

泛化误差

泛化误差（Generalization errors）是指模型在未知数据上的期望误差，即模型对于新数据的预测能力。泛化误差是机器学习中最为重要的概念之一，因为机器学习的目标是构建泛化能力强的模型，而不是仅仅在训练数据上表现良好的模型。泛化误差通常用测试误差来近似估计，但是测试误差只能提供模型的一种局部估计，因此为了更准确地估计模型的泛化误差，需要使用交叉验证等方法。

复杂度与过拟合

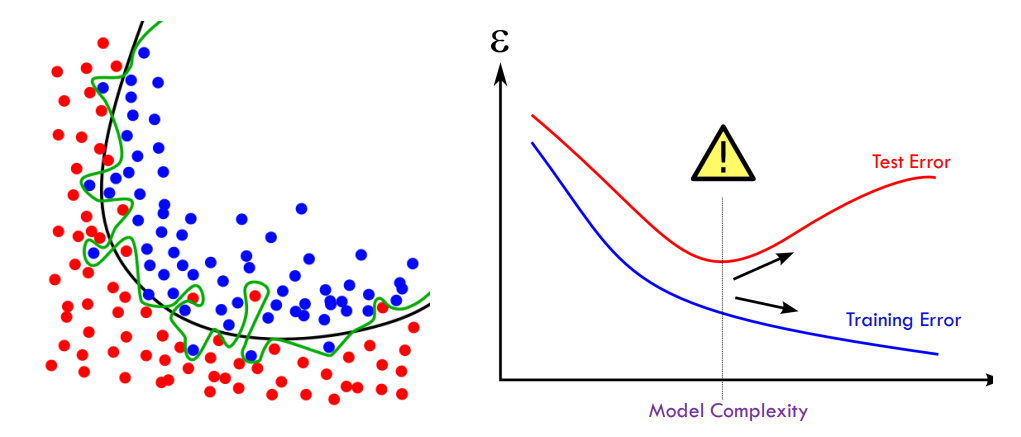
欠拟合：当模型过于简单时，训练和测试误差都很大
过拟合：当建模过于复杂时，训练误差很小，但测试误差很大

给定两个具有相似泛化误差的模型，人们应该更喜欢更简单的模型而不是更复杂的模型
复杂的模型更有可能因数据错误而意外拟合
因此，在评估模型时应包括模型复杂性

规范化

$\lambda$是惩罚权重
取$w$的L2范数作为惩罚项，让系数的取值变得平均。对于关联特征，能够获得更相近的对应系数
L1范数，系数$w$的L1范数作为惩罚项加到损失函数上，由于非零，迫使那些弱的特征所对应的系数变成0，达到特征选择
当𝜆 足够大，相当于：

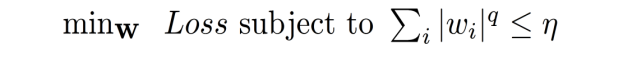
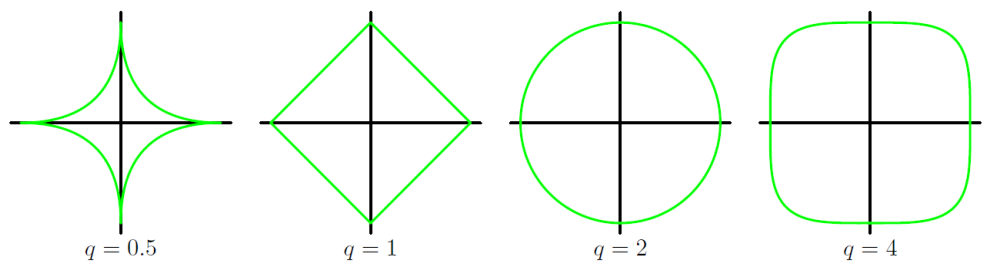
不同q值的正则化项的等高线

最小二乘分类小结

1. 不是进行分类的最佳方法
2. 但是易于训练的封闭式解决方案(闭式解=解析解)
3. 可以与许多经典学习原理联系起来