博主简介：一个爱打游戏的计算机专业学生
博主主页： @夏驰和徐策
所属专栏：算法设计与分析

1.什么是哈夫曼编码？

哈夫曼编码（Huffman coding）是一种用于数据压缩的无损编码方法。它是由David A. Huffman在1952年提出的，被广泛应用于通信和存储领域。

哈夫曼编码通过对不同符号赋予不同长度的编码，使得出现频率高的符号使用较短的编码，而出现频率低的符号使用较长的编码，以此来实现数据压缩。哈夫曼编码的关键思想是利用变长编码来表达符号，使得出现频率高的符号的编码比出现频率低的符号的编码更短，从而减少整体的编码长度。

哈夫曼编码的构建过程如下：
1. 统计符号的出现频率：遍历待编码的符号序列，统计每个符号出现的频率。
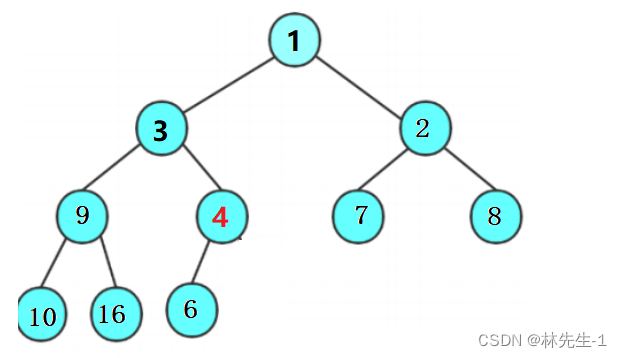
2. 构建哈夫曼树：根据符号频率构建哈夫曼树。频率越高的符号离根节点越近，频率越低的符号离根节点越远。
3. 分配编码：从根节点开始，为哈夫曼树的每个叶子节点分配一个编码。沿着左子树走为0，沿着右子树走为1。最终，每个符号都有一个唯一的二进制编码。
4. 压缩数据：将原始数据中的每个符号替换为对应的哈夫曼编码，从而实现数据的压缩。

由于哈夫曼编码使用变长编码，可以根据符号的出现频率进行最优编码，因此哈夫曼编码可以实现无损压缩，即在解码时完全还原原始数据。哈夫曼编码被广泛应用于数据压缩、图像压缩、音频压缩等领域。

2.什么是前缀码

前缀码（Prefix code）是一种编码方式，其中没有任何一个编码是另一个编码的前缀。换句话说，前缀码中的每个编码都不是其他编码的前缀。

前缀码的主要特点是具有唯一解码性。由于没有编码是其他编码的前缀，所以在解码时可以根据编码的唯一性来还原原始数据，无需使用特殊的结束标记或其他辅助信息。

哈夫曼编码是一种常见的前缀码。在哈夫曼编码中，根据符号出现的频率，将出现频率高的符号赋予较短的编码，而出现频率低的符号赋予较长的编码。由于哈夫曼编码是前缀码，所以在解码时可以通过识别编码的唯一性来还原原始数据。

前缀码具有高效的压缩性能和解码速度。在通信和数据存储中，前缀码常被用于数据压缩、图像压缩、音频压缩等领域，以减少数据的传输和存储成本。

3.如何构造哈夫曼编码？

构造哈夫曼编码的步骤如下：

1. 统计符号的出现频率：遍历待编码的符号序列，统计每个符号出现的频率。可以使用一个频率表或者堆数据结构来记录符号和频率的对应关系。

2. 构建哈夫曼树：根据符号频率构建哈夫曼树。首先，将每个符号视为一个独立的树节点，并根据频率将这些节点组成森林（每个节点是一棵单节点的树）。然后，重复以下步骤直到只剩下一棵树：
- 选择频率最低的两个树节点，将它们作为左右子树创建一个新的父节点，并将父节点的频率设为左右子树节点的频率之和。
- 将新创建的父节点加入到森林中。
- 从森林中移除被合并的两个节点。

3. 分配编码：从哈夫曼树的根节点开始，为每个叶子节点分配一个编码。遍历哈夫曼树的路径，当向左子树移动时，添加一个0到编码中；当向右子树移动时，添加一个1到编码中。最终，每个符号都将有一个唯一的二进制编码。

4. 压缩数据：将原始数据中的每个符号替换为对应的哈夫曼编码，从而实现数据的压缩。

构造哈夫曼编码的关键在于构建哈夫曼树和分配编码的过程。哈夫曼树的构建基于贪心算法，通过合并频率最低的节点来构建树。分配编码时，通过深度优先遍历哈夫曼树的路径来为每个叶子节点分配编码。

注意，构造哈夫曼编码时，为了确保编码的唯一性，需要保证符号的频率已经预先给定，且频率较高的符号具有较短的编码。

4.算法用的类Huffman定义如下：

template<class Type>
class Huffman
{
	friend BinaryTree<int> HuffmanTree(Type[], int);
public:
	operator Type ()const { return weight; }
private:
	BinaryTree<int> tree;
	Type weight;
};

我的理解：

这段代码是一个Huffman编码的实现。Huffman编码是一种用于数据压缩的算法，通过将出现频率较高的字符用较短的编码表示，来实现对数据的高效压缩。

代码中定义了一个名为Huffman的模板类，该类具有一个模板参数Type，表示编码的数据类型。类中有一个友元函数HuffmanTree，返回一个BinaryTree<int>类型的对象，表示Huffman编码树。类中还有一个类型转换运算符，用于将对象转换为Type类型，返回权重(weight)。

模板类Huffman包含以下成员：
- BinaryTree<int> tree: 一个BinaryTree<int>类型的对象，表示Huffman编码树。
- Type weight: 表示权重(weight)，即字符出现的频率或权值。

在实际使用时，可以根据具体的需求实例化Huffman类，并调用HuffmanTree函数来构建Huffman编码树。

5.哈夫曼算法的代码实现：

template <class Type>
BinaryTree<int> HuffmanTree(Type f[], int n)
{
	Huffman<Type>* w = new Huffman<Type>[n + 1];
	BinaryTree<int> z, zero;
	for (int i = 1; i <= n; i++)
	{
		z.MakeTree(i, zero, zero);
		w[i].weight = f[i];
		w[i].tree = z;
	}
	//建立优先队列
	MinHeap<Huffman<Type>>Q(1);
	Q.Initialize(w, n, n);
	//反复合成最小频率树
	Huffman<Type> x, y;
	for (int i = 1; i < n; i++)
	{
		Q.DeleteMin(x);
		Q.DeleteMin(y);
		z.MakeTree(0, x.tree, y.tree);
		x.weight += y.weight;
		x.tree = z;
		Q.Insert(x);
	}
	Q.DeleteMin(x);
	Q.Deactivate();
	delete[]w;
	return x.tree;
}

我的理解：

这段代码实现了Huffman编码树的构建过程。

首先，函数HuffmanTree是一个模板函数，接受两个参数：一个类型为Type的数组f[]，表示每个字符的频率或权值；一个整数n，表示数组中元素的数量。

在函数内部，首先创建了一个长度为n+1的Huffman类型的指针数组w，用于存储Huffman类的对象。然后创建了两个BinaryTree<int>类型的对象z和zero。

接下来，通过一个循环遍历数组f[]，为每个元素创建一个Huffman对象，并将权重设置为对应的频率值，同时将BinaryTree对象设置为z。这样就得到了n个具有权重和二叉树的Huffman对象。

接下来，代码通过创建一个MinHeap对象Q来建立优先队列，用于按照权重值对Huffman对象进行排序和管理。Q.Initialize函数用于初始化优先队列，并将Huffman对象数组w中的元素添加到优先队列中。

然后，代码通过一个循环反复合成最小频率的树。循环中，每次从优先队列中删除权重最小的两个Huffman对象x和y，创建一个新的BinaryTree对象z，将x和y的二叉树作为子树连接到z上，然后将x的权重更新为x和y权重的和，并将z设置为x的二叉树。最后，将更新后的x对象重新插入优先队列中。

最后，从优先队列中删除剩下的最后一个Huffman对象x，将优先队列禁用，释放之前动态分配的内存，并返回x对象的二叉树作为Huffman编码树。

总体而言，这段代码通过构建Huffman对象和使用优先队列来实现了Huffman编码树的构建过程。

6.哈夫曼算法的正确性

哈夫曼算法的正确性可以通过以下两个方面来解释：

1. 哈夫曼编码的前缀码性质：哈夫曼编码是一种前缀码，即没有任何一个编码是其他编码的前缀。这意味着在解码时，我们可以通过唯一性地识别每个编码来还原原始数据，而无需使用特殊的结束标记或其他辅助信息。这个前缀码性质是哈夫曼算法的核心特点之一，它确保了编码和解码的一致性，从而保证了正确性。

2. 哈夫曼树的构建：哈夫曼算法通过构建哈夫曼树来生成编码。在哈夫曼树的构建过程中，通过贪心策略，将频率最低的两个节点合并为一个新节点，并按照频率从小到大的顺序进行合并，直到最终只剩下一个根节点。这个贪心策略确保了生成的哈夫曼树的叶子节点对应于原始符号，并且频率较高的符号位于树的较浅层，频率较低的符号位于树的较深层。因此，编码树的构建确保了频率较高的符号获得较短的编码，而频率较低的符号获得较长的编码。

综上所述，哈夫曼算法的正确性可以通过哈夫曼编码的前缀码性质和哈夫曼树的构建过程来解释。这些特性确保了编码的一致性和最优性，从而实现了正确的数据压缩和解压缩。