边缘化中FEJ图例的理解

news2024/11/28 0:34:18

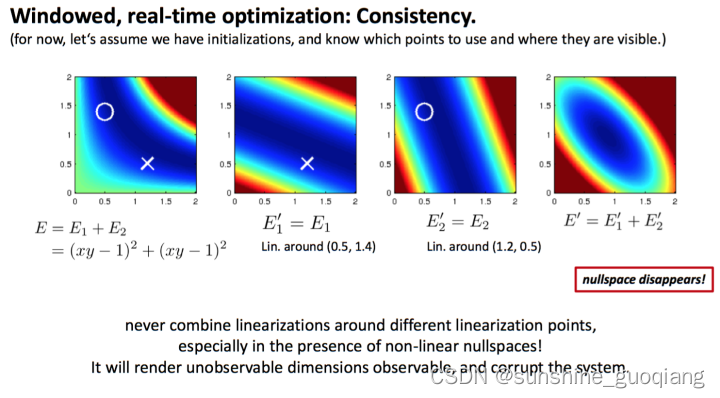
在这里插入图片描述

如图所示，在解释为什么需要FEJ(First Estimation Jacobian)时，通常会将这个图拿出来说事。但是，很多时候只是一笔带过，这个图看的云里雾里的，不是非常明白(可能是我理解力的问题），所以，今天想专门写个笔记记录下对这张图的理解。

非线性优化中， $\Delta x$ 取到最优的点就是： $J^{T}J\Delta x =-J^{T}b$ ，它是从 $F(\Delta x)$ 的泰勒展开式的倒数推导出来的，即 $(J\Delta x - b)^{T}(J\Delta x -b) = [\Delta x J^{T} J \Delta x + 2 J^{T}b \Delta x + b^{2} ]^{'}$ ，从这个式子可以看到，假如把 $\Delta x$ 的分布看成正态分布的话， $J^{T}J$ 就是该正态分布的 $\sigma$ ，即协方差，它决定了 $\Delta x$ 的分布是一条直线还是一个椭圆，因为其他项是线性的，只能影响该分布的朝向、位置等，不会影响形状。

协方差代表了分布在主方向和非主方向上的方差，具体原理可以参考 CodingLabs - PCA的数学原理，如果协方差的通过特征值分解能变成

$\begin{pmatrix} a & 0\\ 0 & b \end{pmatrix}$

，a,b是该协方差的特征值，如果ab都不为0，它的分布就是个椭圆。否则有一个为0，它的分布就是直线。

对于 $E_{1}^{'}$ ，它的

$J^{T}J=\begin{pmatrix} \frac{\partial E}{\partial x} \\ \frac{\partial E}{\partial y} \end{pmatrix} * \begin{pmatrix} \frac{\partial E}{\partial x} & \frac{\partial E}{\partial y} \end{pmatrix} = \begin{pmatrix} -0.3\\-0.84 \end{pmatrix} * \begin{pmatrix} -0.3,-0.84 \end{pmatrix}=\begin{pmatrix} 0.09&0.252\\0.252 &0.7056\end{pmatrix}$

,求它的特征值：

$\begin{vmatrix} 0.09-\lambda & 0.252\\0.252 &0.7056- \lambda \end{vmatrix}=(0.09-\lambda)(0.7056-\lambda)-0.252*0.252=\lambda(\lambda-0.7956)$

即它的特征值是0和0.7956，那么它的分布是条直线。

同理，对于 $E_{2}^{'}$ ,它的 $J^{T}J=\begin{pmatrix} -0.24\\-0.4 \end{pmatrix} * \begin{pmatrix} -0.24 & -0.4 \end{pmatrix}=\begin{pmatrix} 0.0576&0.096\\0.096 &0.16\end{pmatrix}$ ，它的特征值是：0和0.7956，它的分布是一条直线。

对于 $E^{'}$ ,它的 $J^{T}J$ 就是对应 $E_{1}^{'}$ 和 $E_{2}^{'}$ 的 $J^{T}J$ 的和，即 $\begin{pmatrix} 0.09&0.252\\0.252 &0.7056\end{pmatrix}+\begin{pmatrix} 0.0576&0.096\\0.096 &0.16\end{pmatrix}=\begin{pmatrix} 0.1476&0.348\\0.348 &0.8656\end{pmatrix}$ ,它的特征值：

$\begin{vmatrix} 0.1476-\lambda & 0.348\\0.348 &0.8656- \lambda \end{vmatrix}=(0.1476-\lambda)(0.8656-\lambda)-0.348*0.348=\lambda^{2}-1.0132\lambda-0.07664262912$