空调管道的设计:某景区有6个景点,位置分布如下图。
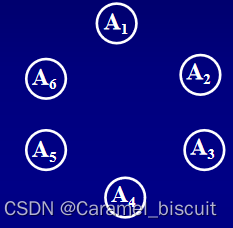
分析者认为:(1) A1与A4, (2) A2与A5, (3) A3与A6间人流较少,其它景点之间人流量大,必须投资铺设空调管道,但要求空调管道间不能交叉。如何设计?
把每个景点分别设为一个点,景点间连线当且仅当两景点间要铺设空调管道。
则原问题的图对应为:
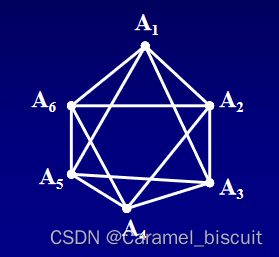
问题转化为:能否把上图画在平面上,使得边不会相互交叉。
若图G可画在一个平面上使除顶点外边不交叉,则称 G可嵌入平面,或称G为可平面图。可平面图G的边不交叉的一种画法称为G的一个平面嵌入,G的平面嵌入表示的图称为平面图。
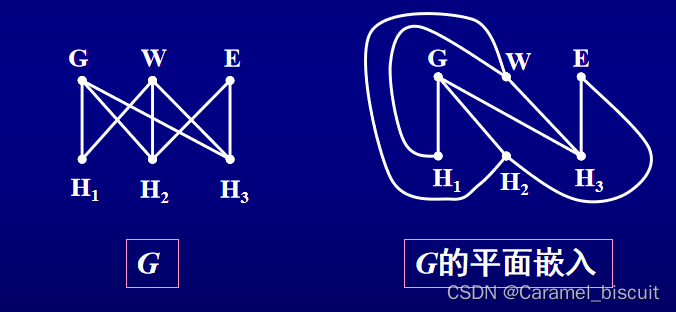
设G是一个平面图,G将所嵌入的平面划分为若干个区域,每个区域的内部连同边界称为G的面,无界的区域称为外部面或无限面。G的面组成的集合用Φ表示。
每个平面图有且仅有一个外部面。
对于平面图来说,割边就是只属于一个面的边。
f是G的一个面,构成f的边界的边数(割边计算2次)称为面f的次数,记为deg(f)
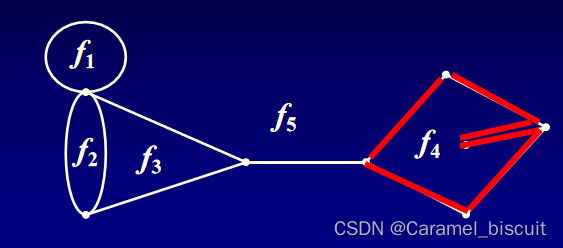
deg(f1)=1
deg(f2)=2
deg(f3)=3
deg(f4)=6
deg(f5)=10
相加为22,正好是边数11的2倍。
设G是具有m条边的平面图,则
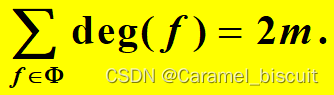
对G的任意一条边e,如果e是某面的割边,那么由面的次数定义,该边给G的总次数贡献2次;如果e不是割边,那么它必然属于是某两个面的公共边,由面的次数定义知,它也给总次数贡献2次。
设G是具有n个点,m 条边,φ个面的连通平面图,则有
n–m+φ=2。