目录
- 数据预处理
- 模型设计
- 训练过程
- 小批量随机梯度下降
用numpy实现神经网络对波士顿房价进行预测
假设房价和各影响因素之间能够用线性关系来描述: y = ∑ j = 1 M x j w j + b y = { \sum_{j=1}^Mx_j w_j} + b y=j=1∑Mxjwj+b
模型的求解即是通过数据拟合出每个 w j w_j wj和 b b b。其中, w j w_j wj和 b b b分别表示该线性模型的权重和偏置。一维情况下, w j w_j wj 和 b b b 是直线的斜率和截距。
线性回归模型使用均方误差作为(Mean Squared Error,MSE)损失函数(Loss),用以衡量预测房价和真实房价的差异,公式如下:
M S E = 1 N ∑ i = 1 N ( Y i ^ − Y i ) 2 MSE = \frac{1}{N} \sum_{i=1}^N(\hat{Yi} - {Y_i})^{2} MSE=N1i=1∑N(Yi^−Yi)2
为什么用L2损失而不是L1损失?
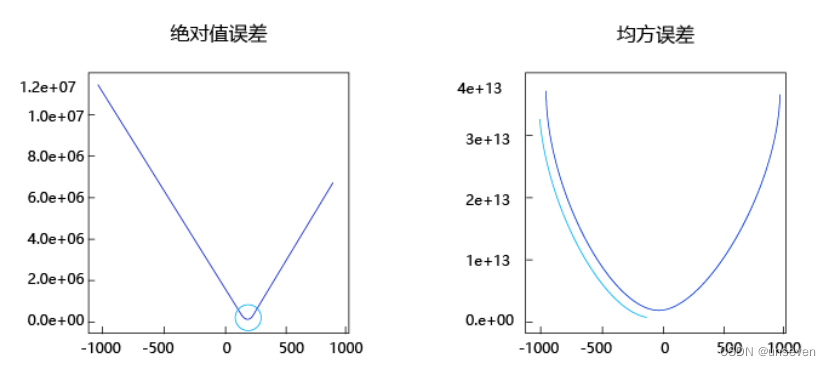
不难看出:
- 曲线的最低点是可导的。
- 越接近最低点,曲线的坡度逐渐放缓,有助于通过当前的梯度来判断接近最低点的程度(是否逐渐减少步长,以免错过最低点)。
而绝对值误差是不具备这两个特性的,这也是损失函数的设计不仅仅要考虑“合理性”,还要追求“易解性”的原因。
数据预处理
先进行数据预处理
所有的数据在house.data文件中,部分数据如下
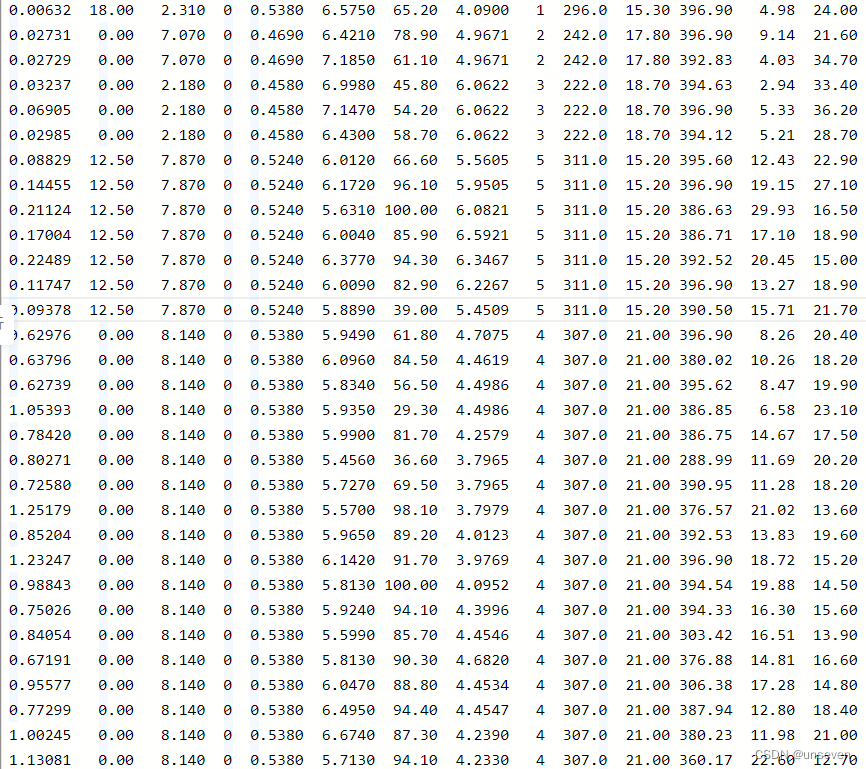
在数据预处理部分需要进行这几个步骤:数据导入、数据形状变换、数据集划分、数据归一化处理和封装load data函数
首先是数据导入,这一块并没有什么难度,从data文件中读取出来即可
# 导入需要用到的package
import numpy as np
import json
# 读入训练数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
data.shape
--------------------------------
(7084,)
这种方式读取数据,将会是一个一维的数据,但是我们需要的是一个二维矩阵,每行为一个数据样本(14个值),每个数据样本包含13个x(影响房价的特征)和一个y(该类型房屋的均价),因此需要数据变换。
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS',
'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])
data.shape
--------------------------------------
(506, 14)
接着是数据集划分,需要训练集和验证集,为什么?
举个例子,上学时总有一些自作聪明的同学,平时不认真学习,考试前临阵抱佛脚,将习题死记硬背下来,但是成绩往往并不好。因为学校期望学生掌握的是知识,而不仅仅是习题本身。另出新的考题,才能鼓励学生努力去掌握习题背后的原理。同样我们期望模型学习的是任务的本质规律,而不是训练数据本身,模型训练未使用的数据,才能更真实的评估模型的效果。
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
training_data.shape
-----------------------------------
(404, 14)
之后进行数据归一化,为什么?
这样做有两个好处:一是模型训练更高效;二是特征前的权重大小可以代表该变量对预测结果的贡献度(因为每个特征值本身的范围相同)。
# 计算train数据集的最大值,最小值
maximums, minimums = training_data.max(axis=0), \
training_data.min(axis=0),
# 对数据进行归一化处理
for i in range(feature_num):
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
到这步已经把数据处理完成了,可以把所有的代码封装到一起,更有复用性,于是封装load_data函数
def load_data():
# 从文件导入数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算训练集的最大值,最小值
maximums, minimums = training_data.max(axis=0), \
training_data.min(axis=0)
# 对数据进行归一化处理
for i in range(feature_num):
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
那么我们获取数据变得极为简单
# 获取数据
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]
模型设计
模型设计是深度学习模型关键要素之一,也称为网络结构设计,相当于模型的假设空间,即实现模型“前向计算”(从输入到输出)的过程。
如果将输入特征和输出预测值均以向量表示,输入特征 x x x有13个向量, y y y有1个向量,那么参数权重的形状是 13 × 1 13\times1 13×1。参数做初始化:W赋值一组随机数。
完整的线性回归公式,还需要初始化偏移量 b b b,同样随意赋初值0。那么,线性回归模型的完整输出是 z = t + b z=t+b z=t+b,这个从特征和参数计算输出值的过程称为“前向计算”。
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,
# 此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
模型设计完成后,需要通过训练配置寻找模型的最优值,即通过损失函数来衡量模型的好坏。训练配置也是深度学习模型关键要素之一。
通过模型计算 x 1 x_1 x1表示的影响因素所对应的房价应该是 z z z, 但实际数据告诉我们房价是 y y y。这时我们需要有某种指标来衡量预测值 z z z跟真实值 y y y之间的差距。对于回归问题,最常采用的衡量方法是使用均方误差作为评价模型好坏的指标,公式为
L o s s = ( y − z ) 2 Loss = (y - z)^2 Loss=(y−z)2
上式中的 L o s s Loss Loss通常也被称作损失函数,它是衡量模型好坏的指标。在回归问题中常用均方误差作为损失函数,而在分类问题中常用采用交叉熵(Cross-Entropy)作为损失函数。
因为计算损失函数时需要把每个样本的损失函数值都考虑到,所以我们需要对单个样本的损失函数进行求和,并除以样本总数 N N N。公式为
L o s s = 1 N ∑ i = 1 N ( y i − z i ) 2 Loss= \frac{1}{N}\sum_{i=1}^N{(y_i - z_i)^2} Loss=N1i=1∑N(yi−zi)2
进一步丰富类
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
类的使用极为方面
net = Network(13)
# 可以一次性计算多个样本的预测值和损失函数
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
print('predict: ', z)
loss = net.loss(z, y1)
print('loss:', loss)
------------------------------------------------------
predict: [[2.39362982]
[2.46752393]
[2.02483479]]
loss: 3.384496992612791
训练过程
求解参数 𝑤 和 𝑏 的数值,这个过程也称为模型训练过程。训练过程是深度学习模型的关键要素之一,其目标是让定义的损失函数尽可能的小,也就是说找到一个参数解 𝑤 和 𝑏 ,使得损失函数取得极小值。
高数知识告诉我们在极小值处导数为0,损失函数取极小值的
w
w
w和
b
b
b应该是下述方程组的解:
∂
L
∂
w
=
0
\frac{\partial{L}}{\partial{w}}=0
∂w∂L=0
∂
L
∂
b
=
0
\frac{\partial{L}}{\partial{b}}=0
∂b∂L=0
将样本数据 ( x , y ) (x, y) (x,y)带入上面的方程组中即可求解出 w w w和 b b b的值,但是这种方法只对线性回归这样简单的任务有效。如果模型中含有非线性变换,或者损失函数不是均方差这种简单的形式,则很难通过上式求解。为了解决这个问题,下面我们将引入更加普适的数值求解方法:梯度下降法。
这种情况特别类似于一位想从山峰走到坡谷的盲人,他看不见坡谷在哪(无法逆向求解出 L o s s Loss Loss导数为0时的参数值),但可以伸脚探索身边的坡度(当前点的导数值,也称为梯度)。那么,求解Loss函数最小值可以这样实现:从当前的参数取值,一步步的按照下坡的方向下降,直到走到最低点。即“梯度下降法(Gradient Descent,GD)”。
参数往哪个地方变是有要求的(往哪边下坡要讲究策略),第一要保证 L是下降的,第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们,沿着梯度的反方向,是函数值下降最快的方向。
上面我们讲过了损失函数的计算方法,这里稍微改写,为了使梯度计算更加简洁,引入因子 1 2 \frac{1}{2} 21(因子不会改变单调性),定义损失函数如下:
L = 1 2 N ∑ i = 1 N ( y i − z i ) 2 L= \frac{1}{2N}\sum_{i=1}^N{(y_i - z_i)^2} L=2N1i=1∑N(yi−zi)2
其中 z i z_i zi是网络对第 i i i个样本的预测值:
z i = ∑ j = 0 12 x i j ⋅ w j + b z_i = \sum_{j=0}^{12}{x_i^{j}\cdot w_j} + b zi=j=0∑12xij⋅wj+b
梯度的定义:
g r a d i e n t = ( ∂ L ∂ w 0 , ∂ L ∂ w 1 , . . . , ∂ L ∂ w 12 , ∂ L ∂ b ) gradient= (\frac{\partial{L}}{\partial{w_0}},\frac{\partial{L}}{\partial{w_1}}, ... ,\frac{\partial{L}}{\partial{w_{12}}} ,\frac{\partial{L}}{\partial{b}}) gradient=(∂w0∂L,∂w1∂L,...,∂w12∂L,∂b∂L)
可以计算出 L L L对 w w w和 b b b的偏导数:
∂ L ∂ w j = 1 N ∑ i = 1 N ( z i − y i ) ∂ z i ∂ w j = 1 N ∑ i = 1 N ( z i − y i ) x i j \frac{\partial{L}}{\partial{w_j}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{w_j}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)x_i^{j}} ∂wj∂L=N1i=1∑N(zi−yi)∂wj∂zi=N1i=1∑N(zi−yi)xij
∂ L ∂ b = 1 N ∑ i = 1 N ( z i − y i ) ∂ z i ∂ b = 1 N ∑ i = 1 N ( z i − y i ) \frac{\partial{L}}{\partial{b}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{b}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)} ∂b∂L=N1i=1∑N(zi−yi)∂b∂zi=N1i=1∑N(zi−yi)
从导数的计算过程可以看出,因子 1 2 \frac{1}{2} 21被消掉了,这是因为二次函数求导的时候会产生因子 2 2 2,这也是我们将损失函数改写的原因。
下面我们考虑只有一个样本的情况下,计算梯度:
L = 1 2 ( y i − z i ) 2 L= \frac{1}{2}{(y_i - z_i)^2} L=21(yi−zi)2
z 1 = x 1 0 ⋅ w 0 + x 1 1 ⋅ w 1 + . . . + x 1 12 ⋅ w 12 + b z_1 = {x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + b z1=x10⋅w0+x11⋅w1+...+x112⋅w12+b
可以计算出:
L = 1 2 ( x 1 0 ⋅ w 0 + x 1 1 ⋅ w 1 + . . . + x 1 12 ⋅ w 12 + b − y 1 ) 2 L= \frac{1}{2}{({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + b - y_1)^2} L=21(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)2
可以计算出 L L L对 w w w和 b b b的偏导数:
∂ L ∂ w 0 = ( x 1 0 ⋅ w 0 + x 1 1 ⋅ w 1 + . . . + x 1 12 ⋅ w 1 2 + b − y 1 ) ⋅ x 1 0 = ( z 1 − y 1 ) ⋅ x 1 0 \frac{\partial{L}}{\partial{w_0}} = ({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_12} + b - y_1)\cdot x_1^{0}=({z_1} - {y_1})\cdot x_1^{0} ∂w0∂L=(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)⋅x10=(z1−y1)⋅x10
∂ L ∂ b = ( x 1 0 ⋅ w 0 + x 1 1 ⋅ w 1 + . . . + x 1 12 ⋅ w 12 + b − y 1 ) ⋅ 1 = ( z 1 − y 1 ) \frac{\partial{L}}{\partial{b}} = ({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + b - y_1)\cdot 1 = ({z_1} - {y_1}) ∂b∂L=(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)⋅1=(z1−y1)
这一段优点绕,但无非就是把z换成w和x,然后和w,x又换成z。
没有必要对每个w单独用for循环求解,基于Numpy广播机制(对向量和矩阵计算如同对1个单一变量计算一样),可以更快速的实现梯度计算。计算梯度的代码中直接用 ( z 1 − y 1 ) ⋅ x 1 (z_1 - y_1) \cdot x_1 (z1−y1)⋅x1,得到的是一个13维的向量,每个分量分别代表该维度的梯度。
例如
# 注意这里是一次取出3个样本的数据,不是取出第3个样本
x3samples = x[0:3]
y3samples = y[0:3]
z3samples = net.forward(x3samples)
gradient_w = (z3samples - y3samples) * x3samples
print('gradient_w {}, gradient.shape {}'.format(gradient_w, gradient_w.shape))
上面gradient_w的每一行代表了一个样本对梯度的贡献。根据梯度的计算公式,总梯度是对每个样本对梯度贡献的平均值。
∂
L
∂
w
j
=
1
N
∑
i
=
1
N
(
z
i
−
y
i
)
∂
z
i
∂
w
j
=
1
N
∑
i
=
1
N
(
z
i
−
y
i
)
x
i
j
\frac{\partial{L}}{\partial{w_j}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{w_j}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)x_i^{j}}
∂wj∂L=N1i=1∑N(zi−yi)∂wj∂zi=N1i=1∑N(zi−yi)xij
我们也可以使用Numpy的均值函数来完成此过程,但引入了一个问题,gradient_w的形状是(13,),而 w w w的维度是(13, 1)。导致该问题的原因是使用np.mean函数时消除了第0维。为了加减乘除等计算方便,gradient_w和 w w w必须保持一致的形状。因此我们将gradient_w的维度也设置为(13,1),代码如下:
z = net.forward(x)
gradient_w = (z - y) * x
# axis = 0 表示把每一行做相加然后再除以总的行数
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
print('gradient_w shape', gradient_w.shape)
计算 𝑏 的梯度的代码也是类似的原理。
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
# 此处b是一个数值,所以可以直接用np.mean得到一个标量
同样把以上过程封装到类中
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
每计算一次梯度后对参数进行一次更新,需要注意两点
- 相减:参数需要向梯度的反方向移动。
- eta:控制每次参数值沿着梯度反方向变动的大小,即每次移动的步长,又称为学习率。
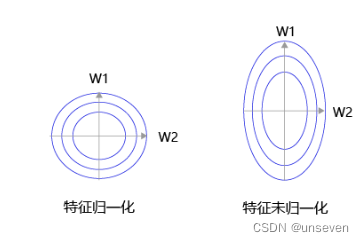
这里再次注意到数据预处理部分的归一化处理,征输入归一化后,不同参数输出的Loss是一个比较规整的曲线,学习率可以设置成统一的值 ;特征输入未归一化时,不同特征对应的参数所需的步长不一致,尺度较大的参数需要大步长,尺寸较小的参数需要小步长,导致无法设置统一的学习率。
至此这个类的各部分就能够完整的实现了
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, x, y, iterations=100, eta=0.01):
losses = []
for i in range(iterations):
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(L)
if (i+1) % 10 == 0:
print('iter {}, loss {}'.format(i, L))
return losses
# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations=1000
# 启动训练
losses = net.train(x,y, iterations=num_iterations, eta=0.01)
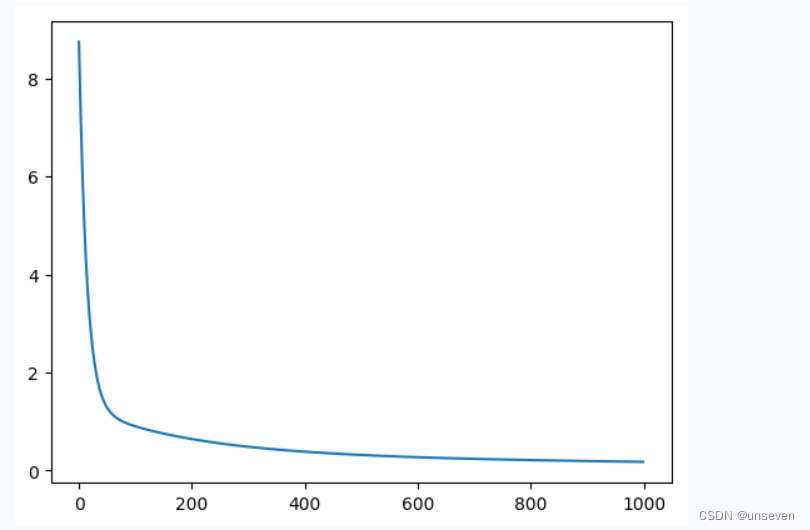
# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()
小批量随机梯度下降
但是还可以继续拓展成小批量随机梯度下降法,之前计算梯度时,我们对所有样本都计算了梯度,然后对梯度求了个均值作为最终的下降方向,每次计算所有样本的梯度将消耗大量时间和计算资源,但是一次只计算一个样本的梯度(随机梯度下降)又怎么保证得到的梯度真的是最好的呢,由一批样本得到的梯度就在这个问题上得到了均衡。
可以想象以下,我们要去一个地方,但是不知道路,向周围的人都问一边其实大可不必,但是只问一个人,又怎么保证他不是乱指的呢,问2到3个人就刚刚好。
对于波士顿房价预测任务数据集而言,样本数比较少,只有404个。但在实际问题中,数据集往往非常大,如果每次都使用全量数据进行计算,效率非常低,通俗地说就是“杀鸡焉用牛刀”。由于参数每次只沿着梯度反方向更新一点点,因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体,基于这部分数据计算梯度和损失来更新参数。
核心概念如下:
- minibatch:每次迭代时抽取出来的一批数据被称为一个minibatch。
- batch size:每个minibatch所包含的样本数目称为batch size。
- Epoch:当程序迭代的时候,按minibatch逐渐抽取出样本,当把整个数据集都遍历到了的时候,则完成了一轮训练,也叫一个Epoch(轮次)。启动训练时,可以将训练的轮数num_epochs和batch_size作为参数传入。
通过大量实验发现,模型对最后出现的数据印象更加深刻。训练数据导入后,越接近模型训练结束,最后几个批次数据对模型参数的影响越大。为了避免模型记忆影响训练效果,需要进行样本乱序操作。
例如:
a = np.array([1,2,3,4,5,6,7,8,9,10,11,12])
print('before shuffle', a)
np.random.shuffle(a)
print('after shuffle', a)
-------------------------------------
before shuffle [ 1 2 3 4 5 6 7 8 9 10 11 12]
after shuffle [ 7 2 11 3 8 6 12 1 4 5 10 9]
完整代码
import numpy as np
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
#np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z-y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epochs, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epochs):
# 在每轮迭代开始之前,将训练数据的顺序随机打乱
# 然后再按每次取batch_size条数据的方式取出
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个mini_batch包含batch_size条的数据
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
#print(self.w.shape)
#print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
format(epoch_id, iter_id, loss))
return losses
# 获取数据
train_data, test_data = load_data()
# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epochs=50, batch_size=100, eta=0.1)
# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()

随机梯度下降加快了训练过程,但由于每次仅基于少量样本更新参数和计算损失ii,所以损失下降曲线会出现震荡。