摘要及声明

1：本文主要利用实际数据进行检验，从定量角度分析均值方差最优化的特性；

2：本文主要为理念的讲解，模型也是笔者自建，文中假设与观点是基于笔者对模型及数据的一孔之见，若有不同见解欢迎随时留言交流；

3：笔者希望搭建出一套交易体系，原则是只做干货的分享。后续将更新更多内容，但工作学习之余的闲暇时间有限，更新速度慢还请谅解；

4：本文主要数据通过数据爬虫获取，模型实现基于python3.8；

利用Markowitz有效前沿做资产配置相信是很多组合管理的必修课程，但是谈到它的缺点却很少有文章分析问题背后的本质原因。本期笔者将利用实际数据进行检验，从定量角度分析均值方差最优化的特性。本文内容如下：

1. 从万众瞩目到弃如敝履

2. 均值方差最优化究竟有多不稳定

2.1 预期和现实

2.2 模型的内生属性

3. 资产过度集中问题

4. 实证检验

4.1 验证低配资产现象

4.2 验证超配资产现象

5. 总结

6. 参考文献

7. 系列精选

1. 从万众瞩目到弃如敝履

19世纪50年代之前，金融更像是一门艺术，大家一拍脑门：“我觉得这个好”。自从1952年均值方差最优化的方案被提出，便打开了利用数学工具认知金融世界的大门，现代金融也和数学深度结合了起来。

均值—方差最优化是Markowitz【2】在1952年提出的风险回报度量模型，可以说是现代资产配置理论（Modern Portfolio Theory，MPT）的先驱和开创者。虽然它的理念和推导十分简单——最优化求解。但在上世纪50年代就把有效前沿算出来了，这简直是开创性的突破。如此厉害的一个理论，如今的现状却是弃如敝履，笔者在实务中几乎见不到有人用那个最原始的模型，更多的还是诸如反向最优化BLM，重抽样，有约束的最优化，分布修正等许许多多的变体。CFA协会【1】列举了它的六个缺点，其中前两条是笔者最常听见的反对声音：1）GIGO（garbage in garbage out），MVO对于输入变量的准确性非常敏感，如果输入变量的准确性较差，那么输出结果的准确性也无法保障；2）MVO 经常出现资产过度集中于几类资产中，而对其他类型资产的分配较少。

然而，针对这两个致命缺点笔者通过数学推理及实证检验后却有不一样的发现，这个实务中几乎见不到人用的古老模型也并非全都一无是处。

2. 均值方差最优化究竟有多不稳定

第一个观点认为，MVO非常不稳定，对于输入变量的准确性非常敏感。比如某个资产预期回报产生一个微小变化，得出的最优化权重就会产生一个大幅变化。造成这种现象的原因无非是两个：1）输入参数具有极大不确定性；2）模型本身非常敏感。

2.1 预期和现实

现实世界中很多金融资产的回报率的确具有极强的不稳定性，以上证指数为例，图一展示了2016年3月至2023年5月上证指数250日移动平均回报率，从-0.2%到0.1%不等，且没有明显趋势。从回报率来看，GIGO这一观点得到有力支持。很多论文批驳均值—方差最优化的一个重要论据就是“事后最优化” ，但是这里其实将预期回报率和真实回报率混为一谈了。

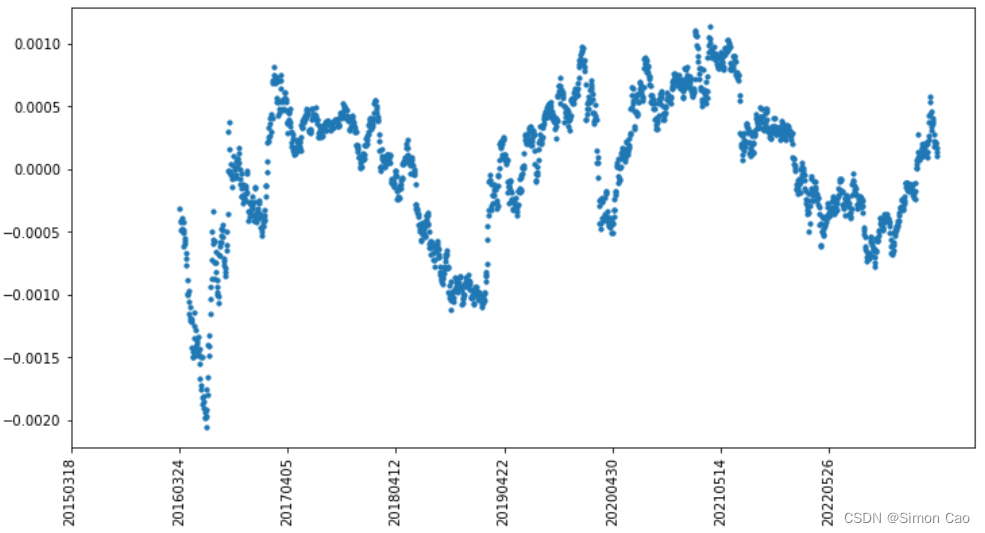
图一：上证指数250日移动平均回报率

如果以-0.2%进行252个交易日的复利，年化收益率为-39.62%；如果以0.1%进行252个交易日的复利，年化收益率为28.64%。这冰红两重天的结果显然都很难作为上证的长期预期年化回报率，因此我们需要防止收益率出现离谱的预期。事实上，预期回报率往往是个相对稳定的常量。例如笔者在GK模型那期计算出的上证指数回报率5.04%，它就可以作为一个相对稳定且合理的预期值。再比如我们可以预期投资级债券收益率4%左右，银行货币理财2%—3%左右，银行存款1%左右，这些都属于相对稳定的预期值。

现在假设笔者满仓梭哈了股票，因为股票有着最高的回报率。一年后上证指数下跌50%，笔者也亏损50%。一个很有意思的结论是：只要做出了离谱的预测，无论用什么方法进行配置大概率都会产生亏损。这其实一个关乎人性的问题：如果你对未来回报率的预测一塌糊涂，那最好的做法其实是不进行交易，而不是遭受亏损后将问题怪罪在均值方差最优化是种垃圾方法。

2.2 模型的内生属性

第二个可能的原因是模型自身的属性造成的，类似的例子还有混沌系统，即初始条件中非常微小的变动也可以导致最终状态的巨大差别。直接上结论：均值方差最优化这个模型本身是具有较强稳定性的。

$f(x) = \frac{R_{p}-R_{f}}{\sigma _{p}}\, \, \, [1]$

均值方差最优化其实无非是想在所有潜在投资组合中找到一个组合，使得函数 $f(x)$ 最大。即使得回报率最大的同时风险最低。

$s.t. \begin{cases} & \text max(R_{p} -R_{f})\\ & \text min(\sigma _{p}) \end{cases}\, \, \, [2]$

但笔者现在关心的是回报率的变化会对模型造成多大影响，这可以直接转化为数学问题，通过导数求解。假设投资组合中，资产的预期回报为 $R=[R_{1}-R_{f}, R_{2}-R_{f},..., R_{n}-R_{f}]$ ，对应权重为 $W=[W_{1},W_{2},...,W_{n}]$ 。直接将[1]式展开：

$R_{p}=R\cdot W$

协方差矩阵和左右两个矩阵的点积其实是组合收益率的方差，求导过程中笔者将之看成常量，不然难以处理：

$Var(R) = W\cdot cov(R)\cdot W^{T}$

$\sigma _{p} = (W\cdot cov(R)\cdot W^{T})^{\frac{1}{2}}$

合并后可以得[3]式：

$\frac{R_{p}}{\sigma _{p}} = \frac{R\cdot W}{(W\cdot cov(R)\cdot W^{T})^{\frac{1}{2}}}\, \, \, \, [3]$

直接对R矩阵求偏导：

$\frac{\partial f(x)}{\partial R} = \frac{\partial (\frac{R\cdot W}{(W\cdot cov(R)\cdot W^{T})^{\frac{1}{2}}})}{\partial R}\, \, \, \, [4]$

[4]化简后可得[5]式：

$\frac{\partial f(x)}{\partial R} =\frac{\partial [(W\cdot cov(R)\cdot W^{T})^{-\frac{1}{2}}\cdot W\cdot R]}{\partial R}$

$\frac{\partial f(x)}{\partial R} = \frac{W}{\sigma} \, \, \, \, [5]$

这个结果说明当模型输入的预期回报变化一个单位时，对模型会产生 $\frac{W}{\sigma }$ 个单位的影响。于是就可以轻易知道均值方差最优化有以下特性：

1）：权重越大，预期回报率R对模型产生影响越大，模型对输入参数越敏感；

2）：标准差越小，预期回报率R对模型产生影响越大，模型对输入参数越敏感；

权重的取值范围是[0,100%]，假设组合中某个资产的权重是100%，那么只有该资产的标准差也是100%的情况下，预期回报变化一个单位，对模型产生的影响才是一个单位。但事实情况是普通资产的标准差往往都比较小，例如图一上证指数日回报率的标准差其实只有1.33%，这样计算出来的偏导数值会非常大。因此，提高模型稳定性就有两个思路：

1）：配置更多资产，降低单个资产潜在的权重分配。两个资产权重平均是50%，四个资产平均是25%，只要组合中资产数量越多，模型w的潜在范围就会越低，此时单个资产对模型的影响越有限，模型稳定性相应也越高。

2）：采用更长周期口径的波动率。上证指数单日的波动率非常小，但如果把这个尺度拉到一年时间，采用年化波动率，此时预期回报对模型造成的影响就会减弱。这也体现了该模型的另一个性质：相比于短周期，从长周期上看，均值—方差最优化有更强稳定性。

3. 资产过度集中问题

这的确是模型导致的，但它是不是该模型的硬伤笔者认为还有待商榷，因为均值—方差最优化目的在于保证收益最高的前提下使得风险最小，它不会无缘无故的就将所有权重全都集中配置在一个资产上。笔者实证检验中发现，即使是相关性非常高，波动率也非常类似的资产，均值方差最优化会倾向于将权重尽可能多的分配给收益率更高的资产。原因其实也非常容易理解：模型将仓位分散配置在两个相关性非常高的资产上其实达不到任何分散化的好处，反而会因为权重分散配置在收益率低的资产上而拉低整体收益率。

另外，对于收益率差不多的资产，即使它们的相关性很弱，均值—方差最优化也倾向于将权重尽可能多的配置给风险低的资产。如果反过来说，均值—方差最优化将某个资产的权重给得非常低，那其实意味着该资产从收益风险最大化得角度上应该从组合中剔除。

集中化头寸的问题笔者暂时没有想到数学手段进行推导验证，主要还是利用实证检验的方式。下面笔者将通过不同类型的基金构建一个投资组合，利用均值—方差最优化寻找最佳权重配置。

4. 实证检验

首先是进行组合构建，笔者随意选取了市场上四只不同类型的开放式基金以代表不同类型的资产，以下是它们的简要信息：

东财代码	简称	类型
000165	国投瑞银策略精选	股票型
000189	易方达丰华债券	债券型
040046	华安纳斯达克100	QDII
070031	嘉实全球房地产	房地产

表一：组合资产构成

数据方面笔者选择通过爬取东方财富网获取这四支基金的净值数据，关于东财这个爬虫程序笔者专门出过一期数据获取的文章（传送门：通过Ajax跳转的网页怎么爬？以东财基金数据为例）。因为数据获取并不是本期的重点，笔者就只放个代码，不做任何技术方面的讲解了。

方便起见，笔者这里简单用这几个资产的历史回报代表未来预期。下面先写一个数据获取程序，nav_data模块输出的结果就是基金净值和涨跌幅数据。

def craw_data(code, page_num):
    url = "http://api.fund.eastmoney.com/f10/lsjz?callback=jQuery18308048793570706319_1685784091702&fundCode="+code+"&pageIndex="+page_num+"&pageSize=500&startDate=&endDate=&"
    headers = {"Referer": "http://fundf10.eastmoney.com/"}
    re = requests.get(url, headers = headers)

    df = re.text
    if len(df) > 300: # 获取内容超过300个字符一般说明成功获得数据了
        df = df.split('LSJZList":[{"')[1].split('}],"FundType"')[0] # 提取数据主体
        df = df.replace('null', '"null"') # 添加“”号方便后续拆分
        df = df.replace('""', '"null"') # 空值统一替换为null

        data_set = []
        for data in df.split('"},{"'):
            data = data.split('","')
            row = {}
            for i in data:
                i = i.split('":"')
                row[i[0]] = i[1]
            data_set.append(row)
        data_set = pd.DataFrame(data_set)
        data_set = data_set[["FSRQ", "JZZZL"]]
        data_set.columns = np.array(["日期", "日增长率"])
        data_set["日增长率"] = data_set["日增长率"].replace("null", 0)
        data_set["日增长率"] = data_set["日增长率"].astype("float")
        data_set.set_index("日期", inplace=True)
        return pd.DataFrame(data_set)
    else: # 没有获得数据
        return pd.DataFrame()
    
    
def nav_data(code):  
    nav_data = pd.DataFrame()
    for page_num in range(1, 1000): # 一般不太可能超过1000页
        data_set = craw_data(code, str(page_num))
        if len(data_set) != 0:
            nav_data = pd.concat([nav_data, data_set], axis=0)
        else:
            break
        print("正在获取{}页, 共获取{}条数据\r".format(page_num, len(nav_data)), end="")
    return nav_data

因为需要获取好几只基金数据，下面写个循环，获取每支基金净值涨跌幅后存入表格：

data_set = pd.DataFrame()
codes = ["000165", "000189", "040046","070031"]
for code in codes:
    print("爬取{}".format(code))
    df = nav_data(code)
    data_set[code] = df["日增长率"]/100
data_set = data_set.dropna()

运行后data_set就存储了四支基金的涨跌幅数据，共1785条数据：

print(data_set)

日期		000165	000189	040046	070031		
2023-06-01	0.0005	0.0007	0.0149	0.0010
2023-05-31	-0.0046	-0.0011	-0.0069	0.0049
2023-05-30	0.0009	0.0002	0.0072	0.0069
2023-05-29	-0.0014	-0.0011	-0.0025	-0.0020
2023-05-26	-0.0014	0.0013	0.0290	0.0140
       ...	    ...	   ...	   ...	   ...
2016-02-05	-0.0067	0.0000	-0.0306	-0.0174
2016-01-29	0.0205	0.0000	0.0198	0.0217
2016-01-22	0.0091	0.0000	0.0246	0.0261
2016-01-15	-0.0246	0.0000	-0.0284	-0.0086
2016-01-13	-0.0197	0.0000	-0.0310	-0.0085
1785 rows × 4 columns

由于需要随机生成权重很多次，这里封装一个权值生成器，方便直接调用：

def weights_mod(num):
    weights = np.random.uniform(0,1,num)
    weights = weights / sum(weights)
    weights = weights.reshape(1,num)
    return weights

下面直接根据均值—方差最优化算法写代码就好，先进行协方差和回报率矩阵计算，这里笔者以250个交易日进行年化：

cov_metric = np.array(data_set.cov())

return_metric = (1 + data_set.mean())**250 - 1
return_metric = np.array(return_metric).reshape(1,len(codes))

调用前面的权值生成器，利用矩阵计算出方差（250日年化），将程序运行中生成的所有数据全部存入字典，最后导入DataFrame数据表results：

results = []
for i in range(10000):
    weights = weights_mod(len(codes))
    variance = weights.dot(cov_metric).dot(weights.transpose()) * (250**(0.5))
    r = return_metric.dot(weights.transpose())
    result = {"r": float(r), "var": float(variance)}
    for w in range(len(codes)): result["weight{}".format(w+1)] = weights.reshape(len(codes))[w] 
    results.append(result)
    print("随机第{}次\r".format(i), end="")
results = pd.DataFrame(results)

设置无风险利率为1.97%（6月份1年期国债利率），直接利用表格计算出夏普比率：

rf = 0.0197 
results["sharp_ratio"] = (results["r"] - rf) / (results["var"]**0.5)
results = results.sort_values("sharp_ratio", ascending=False) # 按夏普比率从大到小排序
results.index = range(len(results))

记录一下夏普比率最大点的坐标值和无风险利率的坐标值，方便一会儿标记在图上：

cml_x = [0, (results["var"]**0.5)[0]]
cml_y = [rf, results["r"][0]]

可视化，运行后得图二：

plt.scatter(results["var"]**0.5, results["r"], s=0.1)
plt.scatter(cml_x[1], cml_y[1], color="red", linewidths=0.05, label="Optimal_point")
plt.legend()
plt.show()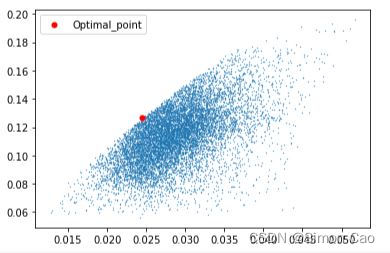

图二：组合分布图与市场组合

当然，也可以将CML线展示到图上，CML线与有效前沿的切点，即使得夏普比率最大的市场组合（Market Portfolio），如图三：

plt.scatter(results["var"]**0.5, results["r"], s=0.2)
plt.plot(cml_x, cml_y, label="CML", color = "orange", linewidth=2)
plt.scatter(cml_x[1], cml_y[1], color="red", s=20, label="Optimal_point")
plt.legend()
plt.show()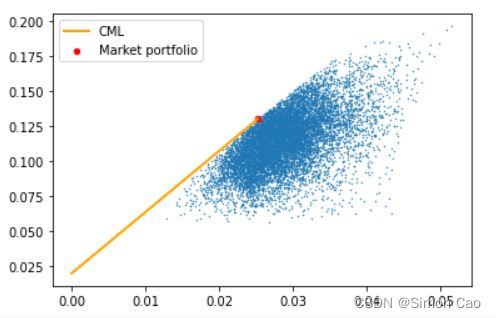

图三：CAL线与与市场组合

至此，均值—方差最优化就全部推导完成了，但还需要进一步验证。

4.1 验证低配资产现象

根据输出的模型参数表可以看到各个资产的权重配置是怎么样的：

print(results.head())

         r       var    weight1   weight2   weight3   weight4  sharp_ratio
0  0.129930  0.000637  0.349491  0.346882  0.302574  0.001053     4.366768
1  0.143658  0.000807  0.434402  0.217759  0.347806  0.000034     4.362942
2  0.134730  0.000696  0.401010  0.291464  0.307251  0.000275     4.361566
3  0.131492  0.000657  0.372430  0.324906  0.300941  0.001724     4.361433
4  0.131327  0.000655  0.334924  0.342503  0.319018  0.003555     4.360497

可以看到，算法对前三个资产进行了非常均匀的配置，但是在第四个资产所配置的权重几乎忽略不计。这似乎可以体现均值—方差最优化配置的资产过度集中问题，但还是笔者所说的观点：算法不会无缘无故低配某个资产。

拉出四个资产的回报率比较一下会发现，第四个资产与第二个资产的回报率是非常接近的，都在5.5%左右。但第二个资产是债券类型，第四个则是房地产类型，房地产的波动率却比债券资产高了3.66倍（1.17%/0.32% = 3.66）。因此，均值—方差最优化不会无缘无故将房地产基金的权重配置得如此之少——同样都是5%左右的回报率，房地产的风险却高了3倍。

names = ["国投瑞银策略精选","易方达丰华债券","华安纳斯达克100","嘉实全球房地产",]
sigma = [data_set["000165"].std(), data_set["000189"].std(),data_set["040046"].std(),data_set["070031"].std()]
indicator = pd.DataFrame(index=names, columns=["r"], data=return_metric.reshape(4,1))
indicator["sigma"] = sigma
indicator["Sharp ratio"] = (indicator["r"]-rf)/indicator["sigma"]

                        r	      sigma	   Sharp ratio
国投瑞银策略精选	0.134494	0.009353	12.273995
易方达丰华债券	    0.055381	0.003192	11.179755
华安纳斯达克100	    0.210381	0.014172	13.454739
嘉实全球房地产	    0.055736	0.011693	3.081727

再从相关性看，嘉实全球房地产其实和其它三支基金的相关性都比较低，总结起来就得出前文笔者的结论：对于收益率差不多的资产，即使它们的相关性很弱，均值—方差最优化也倾向于将权重尽可能多的配置给风险低的资产。

def rho_mod(x, y):
    cov = 0
    for i in range(len(x)):
        cov += (x[i]-np.mean(x))*(y[i]-np.mean(y))
    cov = cov/(len(x)-1)
    return cov/(x.std()*y.std())


names = ["国投瑞银策略精选&嘉实全球房地产","易方达丰华债券&嘉实全球房地产","华安纳斯达克100&嘉实全球房地产"]
rho = [cov_mod(data_set["000165"], data_set["070031"]), cov_mod(data_set["000189"], data_set["070031"]),
      cov_mod(data_set["070031"], data_set["040046"])]
indicator = pd.DataFrame(index=names, columns=["rho"], data=np.array(rho).reshape(3,1))

                                    rho
国投瑞银策略精选&嘉实全球房地产	0.142926
易方达丰华债券&嘉实全球房地产	0.158990
华安纳斯达克100&嘉实全球房地产	0.624338

4.2 验证超配资产现象

另一个极端是均值—方差最优化超配某个资产。在刚才的例子中，股票，债券和海外市场指数所配置的权重都是30%几，如果刨去房地产，均值—方差最优化其实将笔者这个组合配置得非常均衡。

为了说明超配现象的原因，笔者故意在组合中加入两个一模一样的资产，然后强行指定其中一个资产的收益率为两倍。请注意，以上操作是为了说明超配资产现象的原因，该组合其实是笔者构建的虚拟组合，现实中并不存在。下面在组合中放两个一模一样的资产，分别加后缀A和B区分。

data_set = pd.DataFrame()
codes = ["000165A", "000165B", "040046","070031"]
for code in codes:
    print("爬取{}".format(code))
    df = nav_data(code[:6])
    data_set[code] = df["日增长率"]/100
data_set = data_set.dropna()

下面强行指定第一个资产的收益率是原来的两倍，第二个资产变为原来的一半：

return_metric = (1 + data_set.mean())**250 - 1
return_metric = np.array(return_metric).reshape(1,len(codes))

print("原始回报率：", return_metric)
return_metric[0][0] = return_metric[0][0] * 2
return_metric[0][1] = return_metric[0][1] * 0.5
print("假定回报率：", return_metric)

原始回报率： [[0.19116059 0.19116059 0.19553582 0.05625486]]
假定回报率： [[0.38232119 0.0955803  0.19553582 0.05625486]]

下面进行最优化求解，得到前五行模型参数及各资产指标如下，模型可视化输出为图五：

        r       var     weight1   weight2   weight3   weight4   sharp_ratio
0  0.342589  0.001274  0.809777  0.001645  0.159597  0.028981     9.047138
1  0.333181  0.001207  0.751211  0.000290  0.229533  0.018965     9.022467
2  0.337886  0.001256  0.779402  0.013366  0.193627  0.013605     8.978015
3  0.337694  0.001260  0.771589  0.018613  0.209057  0.000741     8.957808
4  0.327147  0.001199  0.720821  0.015426  0.253086  0.010667     8.878080


                        r	      sigma	   Sharp ratio
国投瑞银策略精选A	0.382321	0.010325	35.121594
国投瑞银策略精选B	0.095580	0.010325	7.349369
华安纳斯达克100	    0.195536	0.013176	13.345208
嘉实全球房地产	    0.056255	0.010868	3.363446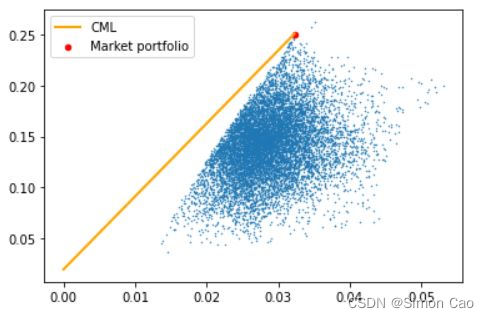

图五：假想组合的最优化模型

可以看出，虽然国投瑞银策略精选AB都是同一支基金（相关系数=1，波动率也完全相等），但模型将权重完全配置到A基金上，B基金几乎没有配置多少权重。这便是笔者之前总结的那条性质：如果有两个相关性非常高，波动率也非常类似的资产，均值方差最优化会倾向于将权重尽可能多的分配给收益率更高的资产。依然回归到那个最根本的结论上：算法不会无缘无故低配某个资产。

5. 总结

本文通过数学推导和实证检验验证了均值—方差最优化模型的相关特性。笔者发现均值—方差最优化的敏感性很大程度上却决于权重和标准差的大小：1）权重越大，预期回报率R对模型产生影响越大，模型对输入参数越敏感； 2）标准差越小，预期回报率R对模型产生影响越大，模型对输入参数越敏感；针对这两个特点，笔者认为可以往组合中添加更多资产，降低单个资产的潜在权重分配及采用更长周期口径的波动率来提高模型整体稳定性。针对均值—方差最优化导致资产配置过度集中问题，均值—方差最优化目的在于保证收益最高的前提下使得风险最小，它不会无缘无故的就将所有权重全都集中配置在一个资产上。笔者在实证检验中发现，如果相关性非常高，波动率也非常类似的资产，均值方差最优化会倾向于将权重尽可能多的分配给收益率更高的资产。对于收益率差不多的资产，即使它们的相关性很弱，均值—方差最优化也倾向于将权重尽可能多的配置给风险低的资产。

6. 参考文献

【1】：CFA Institute, 2020. "Mean Variance Optimization". CFA Study Guide. https://cfastudyguide.com/mean-variance-optimization/

【2】：Markowitz，H. 1952. "Portfolio selection". The Journel of Finance. 7(1). 77-91. https://doi.org/10.1111/j.1540-6261.1952.tb01525.x

7. 系列精选

往期精选
系列	文章传送门	实现方式
权益投资	实现GGM的理想国	Python
	PB指标与剩余收益估值	Python
	Fama-French及PSM	Python
	GK模型看投资的本质	Python
	增速g的测算	Python
	PE指标平滑	Python
	PE Band	Python
	分类树算法	R
	蒙特卡洛模拟	Python
	全连接神经网络模型	Python
组合管理	券商金股哪家强——信息比率	Python
	从指数构建原理看待A股的三千点魔咒	Python
	决策树学习基金持仓并识别公司风格类型	R
杂谈类	垃圾公司对回报率计算的影响几何	Python
	市场预测美联储加息的有效性几何	Python
	市场风险分析	Python
	金融危机模拟	Python