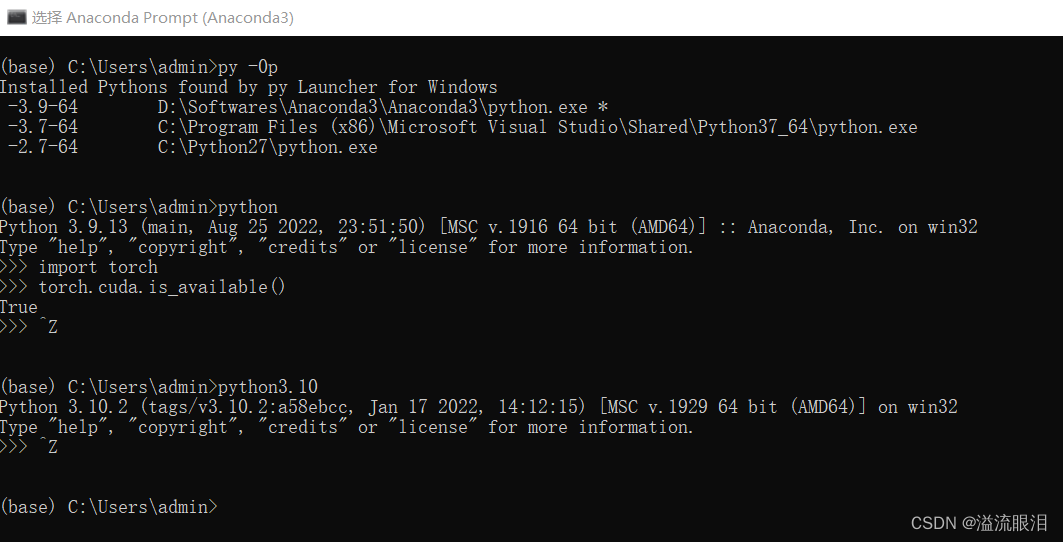
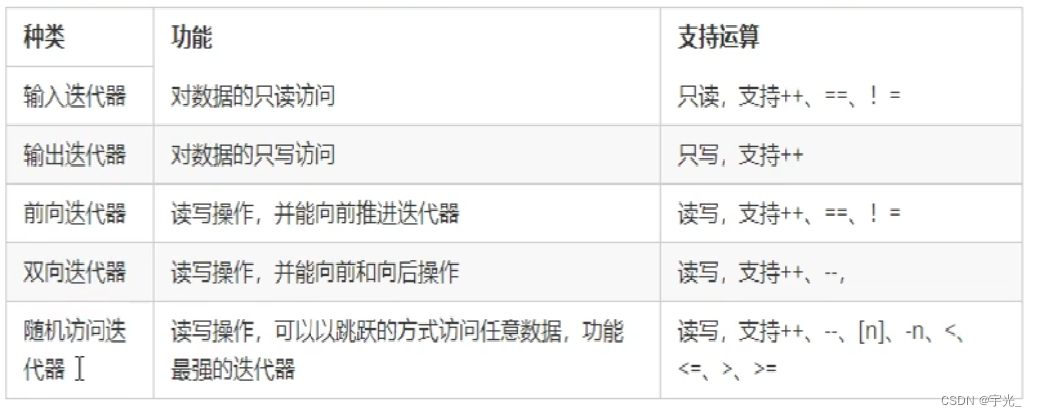
图裂参考原文:https://www.cnblogs.com/odesey/p/16937124.html
1. 为什么使用 Kalman Filters?
1.1 什么是 Kalman Filters?
Kalman Filters 是一种优化估计算法。下面使用使用两个例子说明 Kalman Filters 的用处。
例子1:
用来说明: 在系统的状态无法直接被测量时候, Kalman Filters 如何来估算系统状态。
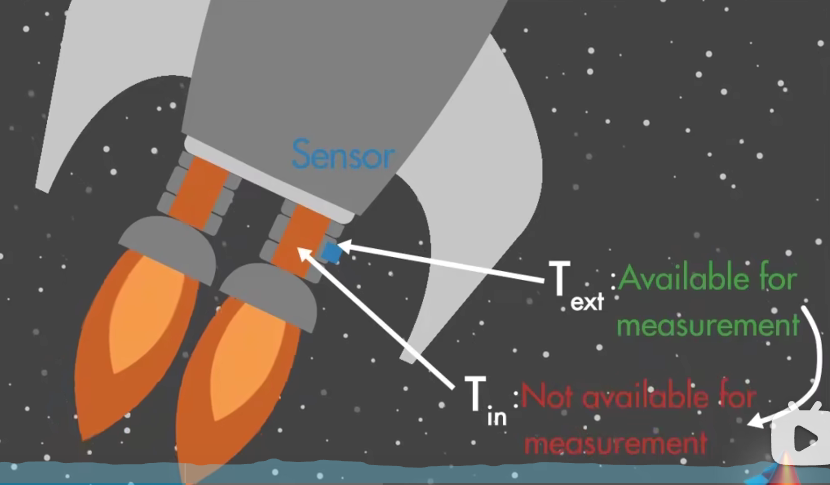
对于飞船的燃烧室,需要监控燃烧室的温度,但是内部温度太高会烧坏传感器,因此只能测量外部温度,那么如何根据测量的外部温度,估计内部问题呢?可以使用 Kalman Filters 利用间接的测量温度,估计内部的温度。
例子2:
用来说明: 使用 Kalman Filters, 通过组合多种可能受到噪音影响的数据源,来估计系统的状态。
如何估计汽车的位置?
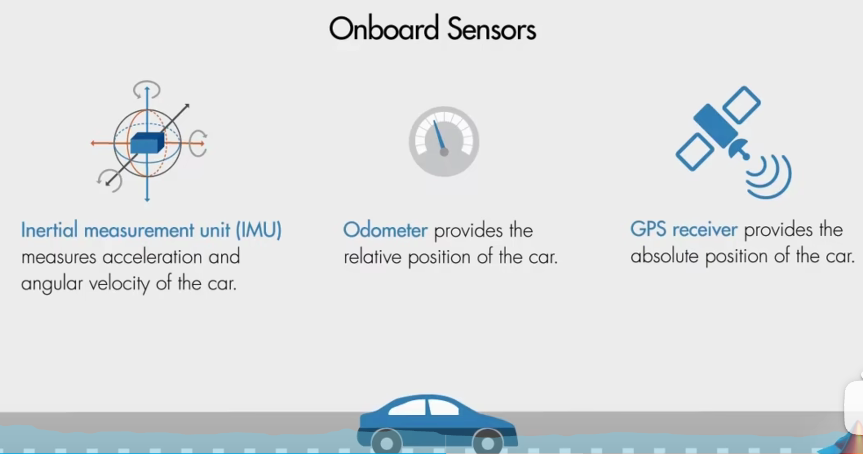
数据1: 车载传感器 惯性测量单元(IMU), 使用加速度计和陀螺仪来测量汽车的加速度和角速度。
数据2: 里程表,测量汽车行驶的相对距离。
数据3: GPS 接收器接收来自卫星的信号,定位汽车在地球表面的位置。

- 如果汽车经过一个长的隧道,在隧道中难以使用 GPS 估计位置,因为接收器和卫星的通信被挡住了。
- 使用 IMU 提供的加速度计算距离(求二次积分),但是小的误差会随着时间不断累积,从而偏差越来越大。
- 结合 IMU 和里程表,但里程表读数会受到轮胎压力和道路情况的影响。
总结:
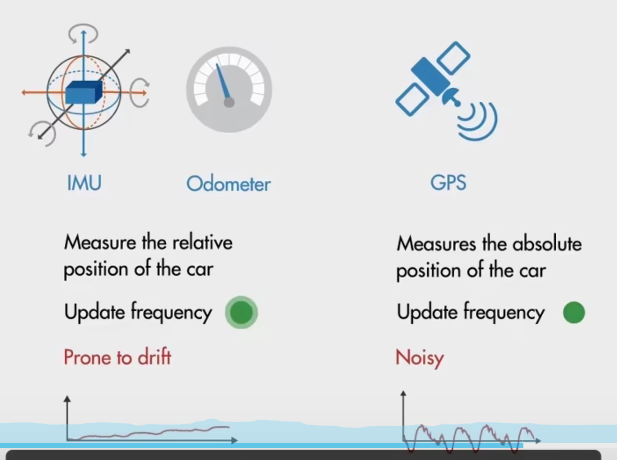
- IMU 可以测量汽车的相对位置,可以快速更新,但是容易漂移。
- GPS 提供绝对位置,更新的慢,并可能存在噪音。
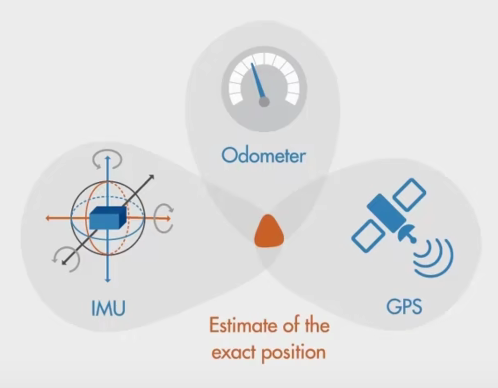
使用 Kalman Filters 结合三个测量值,得到汽车最合适的估算位置。
1.2 Kalman Filters 来源?

优化估计算法:可以在有噪声的情况下,来预测感兴趣的参数,如位置,速度和方向等。
制导和导航控制系统。
在阿波罗登月项目中,使用 Kalman Filters 来估算载人航天器往返月球的轨迹。
1.3 总结

Kalman Filters 是一种设计最优状态观测器的方法。下一节会学习状态观测器。讨论最佳状态观测器。
2. 状态观测器?
定义: X ^ \hat{X} X^ 为估计状态。
例子:测量飞船燃烧室的温度。
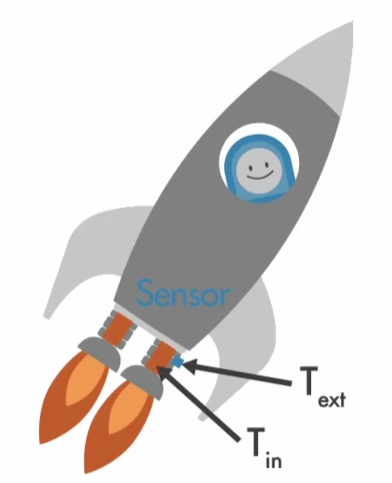
内部温度为: T i n T_{in} Tin, 外部温度为: T e x t T_{ext} Text。
燃油流量为: W f u e l W_{fuel} Wfuel。
通过对真实燃油系统建立数学模型。那么可以通过该数学模型可以估计系统的内部状态了吗?答:不可以。因为数学模型只是真是系统的近似。如果数学模型是真实系统的完美模型,没有任何不确定性,并且真实系统和数学模型具有相同的初始条件,那么数学模型估算的外部测量值: T ^ e x t \hat{T}_{ext} T^ext 就会与真实的外部测量值: T e x t T_{ext} Text 相等,那么模型估算的内部温度值: T ^ i n \hat{T}_{in} T^in 就会与真实的内部温度值: T i n T_{in} Tin 相等。但是实际上是不可能有完美的模型,即数学模型估算的外部测量值: T ^ e x t \hat{T}_{ext} T^ext 会与真实的外部测量值: T e x t T_{ext} Text 有误差。因此需要使用状态观测器来估算系统的内部状态。
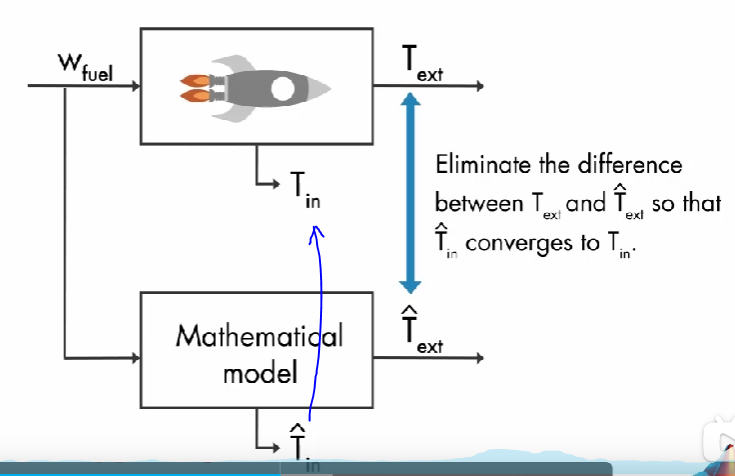
状态观测器原理:如上图所示,目标是数学模型估算的外部测量值: T ^ e x t \hat{T}_{ext} T^ext 与真实的外部测量值: T e x t T_{ext} Text 相等,表示数学模型收敛到了真实系统,那么模型估算的内部温度值: T ^ i n \hat{T}_{in} T^in 就能收敛到 真实的内部温度值: T i n T_{in} Tin。
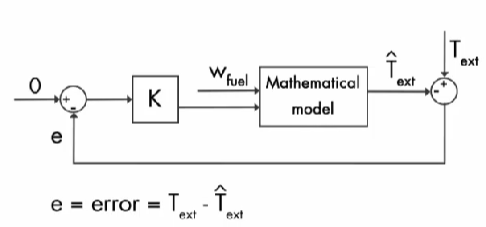
反馈控制系统,我们使用 控制增益 K 试图控制 数学模型估算的外部测量值: T ^ e x t \hat{T}_{ext} T^ext 与真实的外部测量值: T e x t T_{ext} Text 之间的误差为 0。
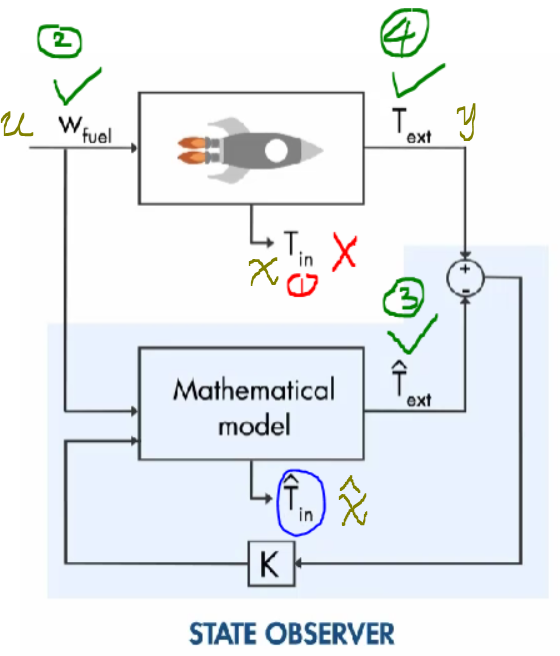
将该反馈控制系统更新到上面图中,蓝色阴影部分为 状态观测器。通过反馈控制,消除数学模型估算的外部测量值: T ^ e x t \hat{T}_{ext} T^ext 与真实的外部测量值: T e x t T_{ext} Text 之间的误差。那么模型估算的内部温度值: T ^ i n \hat{T}_{in} T^in 就会收敛到 真实的内部温度值: T i n T_{in} Tin。
总之:
- 无法测量真实系统内部的温度
- 但是知道给火箭提供了多少燃料
- 因此可以建立 燃料和估算的外部温度的数学模型,得到估算的外部温度
- 结合测量的外部温度值来估计系统内部的温度
问题是如何选择控制增益 K 使得测量的外部温度和模型估算的外部温度之间的误差最小?
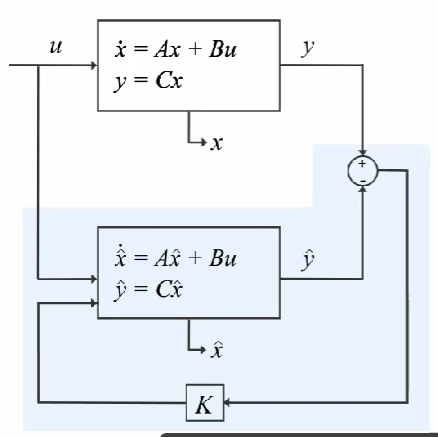
整理公式得到如下结果:
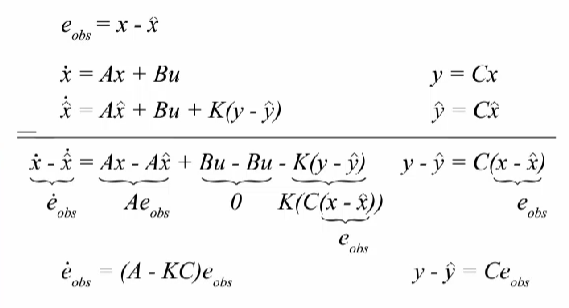
上述等式的解是一个指数函数,这意味着如果 A-KC<0, 那么模型估算的内部温度值 x ^ \hat{x} x^: T ^ i n \hat{T}_{in} T^in 与 真实的内部温度值 x x x: T i n T_{in} Tin 之间的误差会随着时间而降低。 x ^ \hat{x} x^ 最终会收敛到 x x x。
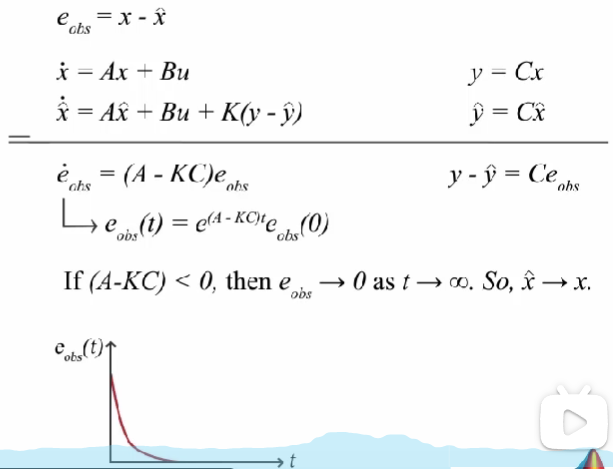
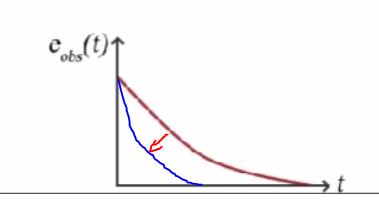
你或许会疑问是否需要 KC 项,即没有反馈回路,即数学模型没有 K ( y − K(y- K(y−\hat{x})$ ,也会得到一个误差衰减的指数函数。给状态观测器建立反馈回路的重要性在于 : 我们可以通过选择相应的控制增益 K 控制误差函数的衰减率。如果 衰减率只取决于 矩阵 A, 如果数学模型中存在一些不确定性,表示并不知道真实的 A,那么就无法控制误差衰减的速度。使用反馈控制增益可以更好的控制这些方程,从而更快的消除误差。误差消除的越快,估算的状态 x ^ \hat{x} x^ 收敛到 真实状态 x x x 的速度就会越快。
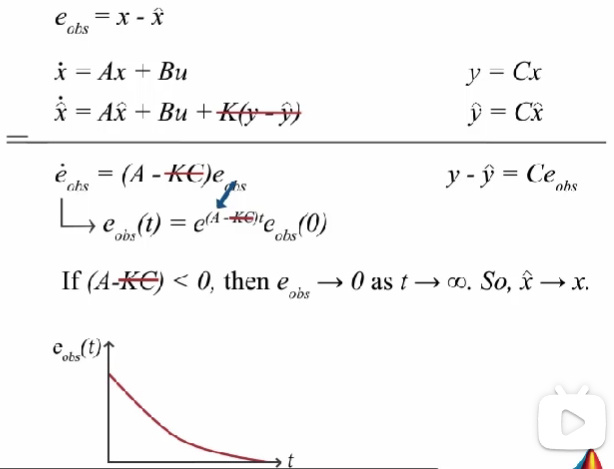
选择反馈控制增益 K 的最佳方法就是 Kalman Filters。
参考
https://www.bilibili.com/video/BV1V5411V72J?p=2


![[附源码]Python计算机毕业设计SSM精品旅游项目管理系统(程序+LW)](https://img-blog.csdnimg.cn/54c7a48139864719ba1fd44bade6bfdf.png)