二叉树的链式结构 - C语言（含有大量递归）

news2024/11/29 8:51:39

目录：

🍔前言

🍔二叉树链式结构的实现

🍟基本构架

😍代码：

🍔二叉树的遍历

🍟前序遍历

🍟中序遍历

🍟后序遍历

🍟层序遍历

🔴层序遍历的思路及代码

🍔 构建二叉树

 😍代码：

🍔二叉树销毁

😍代码：  

🍔二叉树节点个数

😍代码：

🍔二叉树叶子节点个数

😍代码：

🍔二叉树第k层节点个数

😍代码： 

🍔二叉树查找值为x的节点

😍代码：

🍔判断二叉树是否是完全二叉树

😍代码：

😍二叉树的链式结构所有代码汇总😍

✅BinaryTree.c

✅Queue.c

🍔前言

        🥰我们学习完二叉树的“堆”以及堆的应用以后还有一个在平时面试题目中出现频率也非常高的结构等着我们呢，那就是—二叉树的链式结构（二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系）链式结构又分为二叉链和三叉链，当前我们使用的都是二叉链，后面的博客（红黑树等会用到三叉链）各位客官老爷，关注一下后续会更新呦！！！🥰🥰

🍔二叉树链式结构的实现

🍟基本构架

🥝在看二叉树基本操作前，再回顾下二叉树的概念

🔴二叉树是：

⭕ 空树
⭕ 非空：根节点，根节点的左子树、根节点的右子树组成的。

✅从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。

😍代码：

typedef int BTDataType;  //记录树内数据类型，方便后面修改
typedef struct BinaryTreeNode
{
	BTDataType data;  //记录节点
	struct BinaryTreeNode* left; //指针指向左子树
	struct BinaryTreeNode* right;//指针指向右子树
}BTNode;  //结构体的名字

      💧运用上面的这些代码，可以记录一颗二叉树的所有节点，所有推论也从这个地方出来了。后面也会有很多的结构跟这个有关。

🍔二叉树的遍历

     🍪学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

🍟前序遍历

    🚩前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。（根——左子树——右子树）

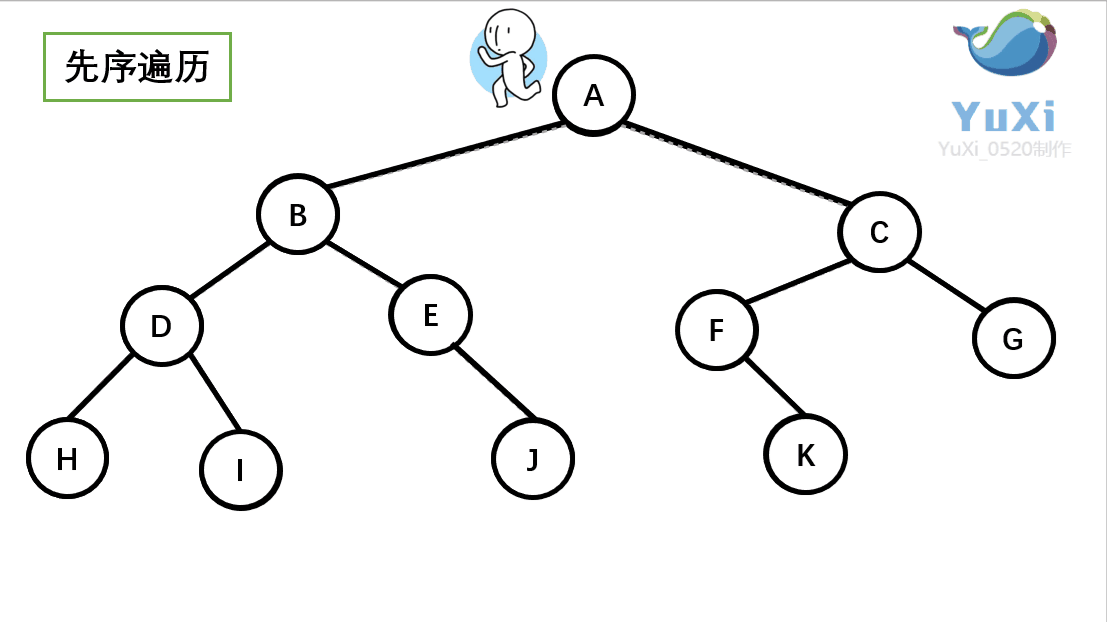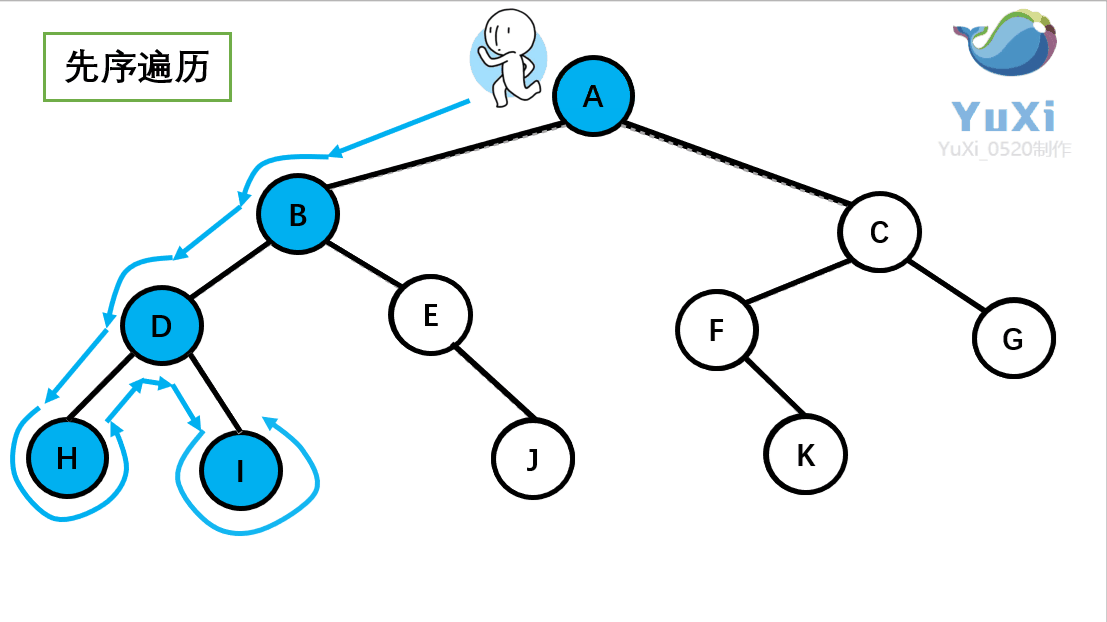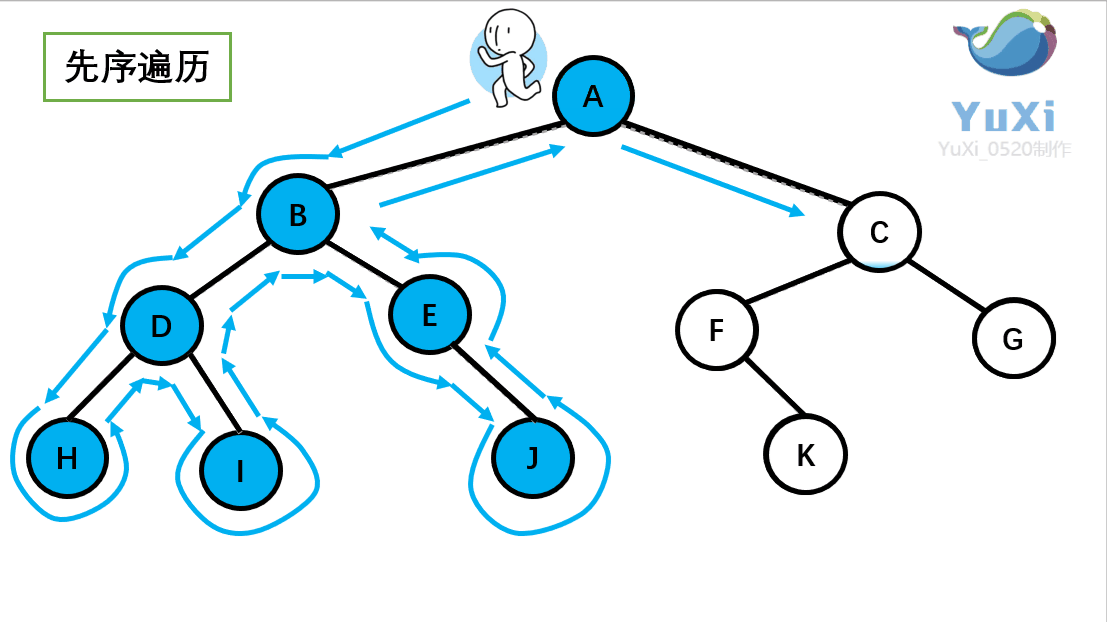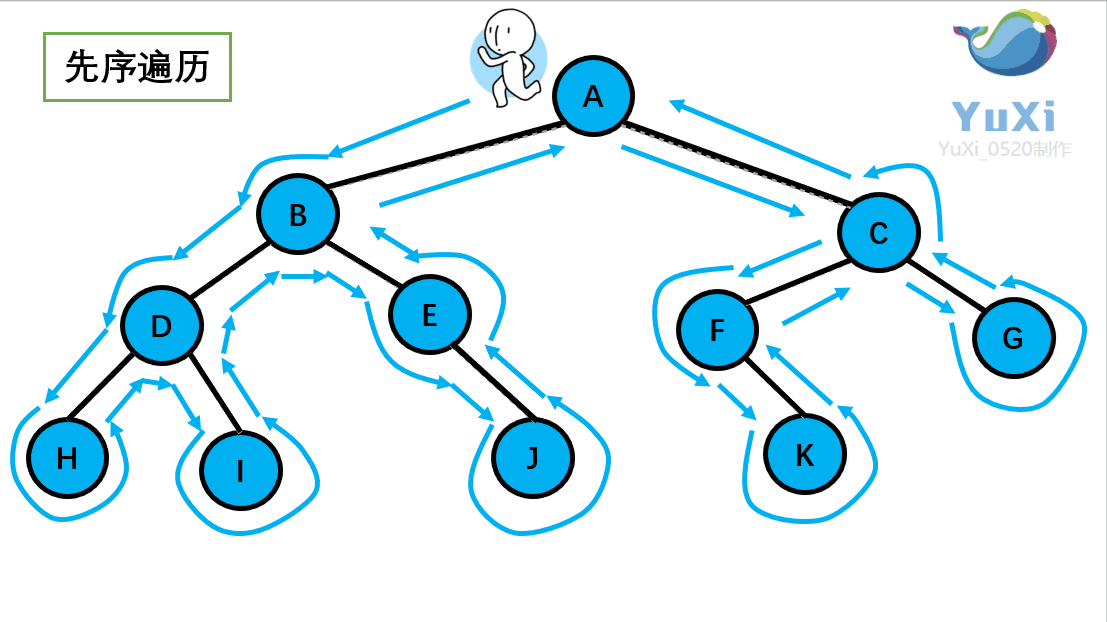
 数据结构——二叉树先序、中序、后序及层次四种遍历（C语言版）_中序遍历_正弦定理的博客-CSDN博客

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

🍟中序遍历

         🚩中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。（左子树——根——右子树）

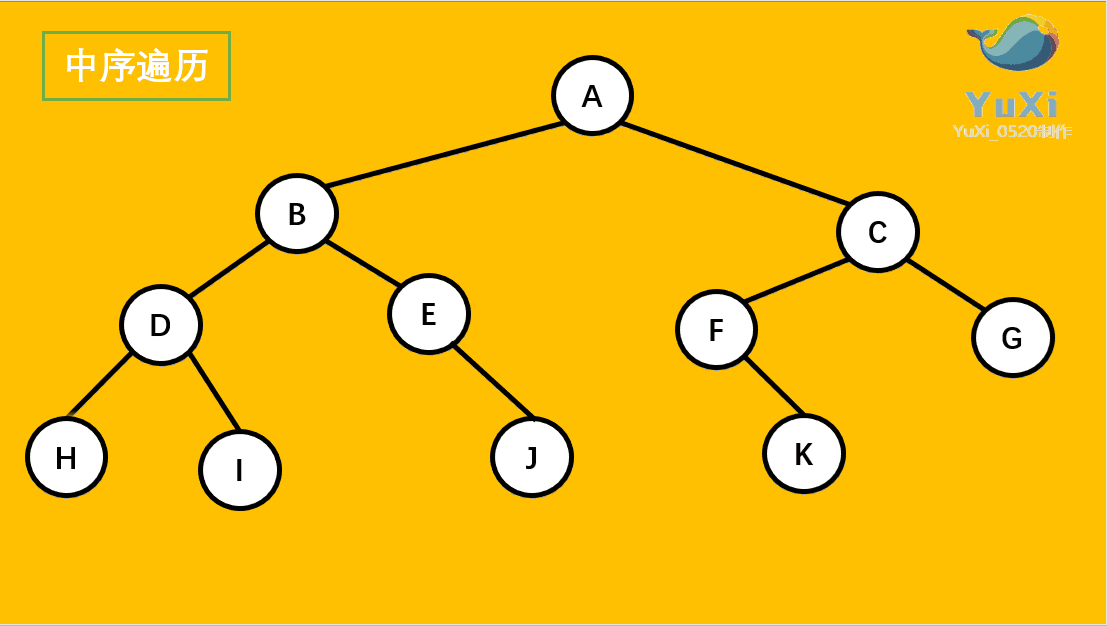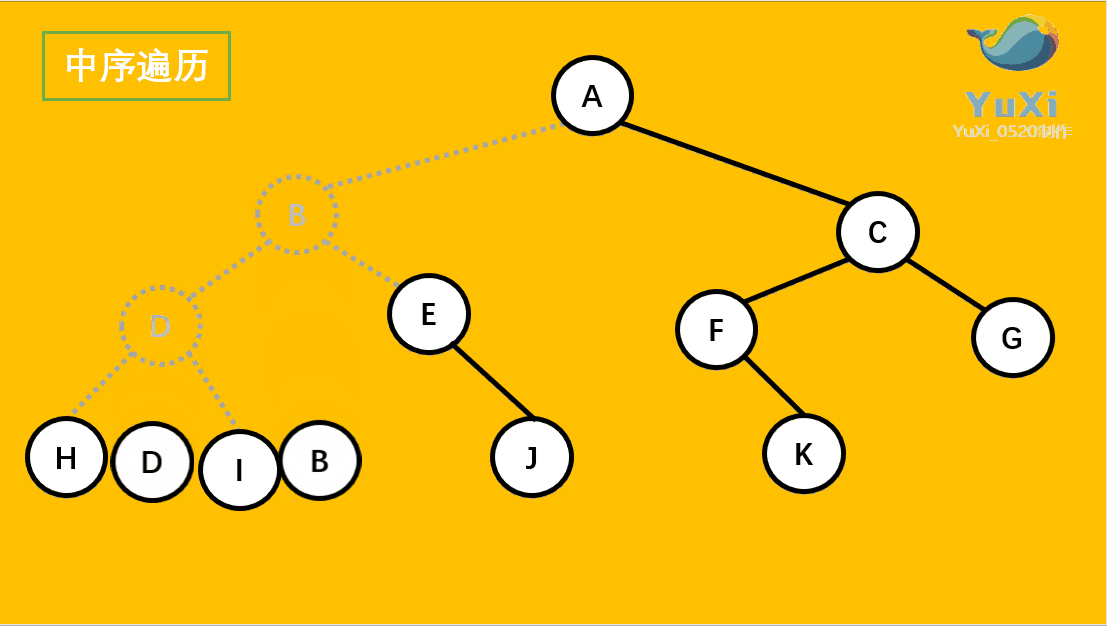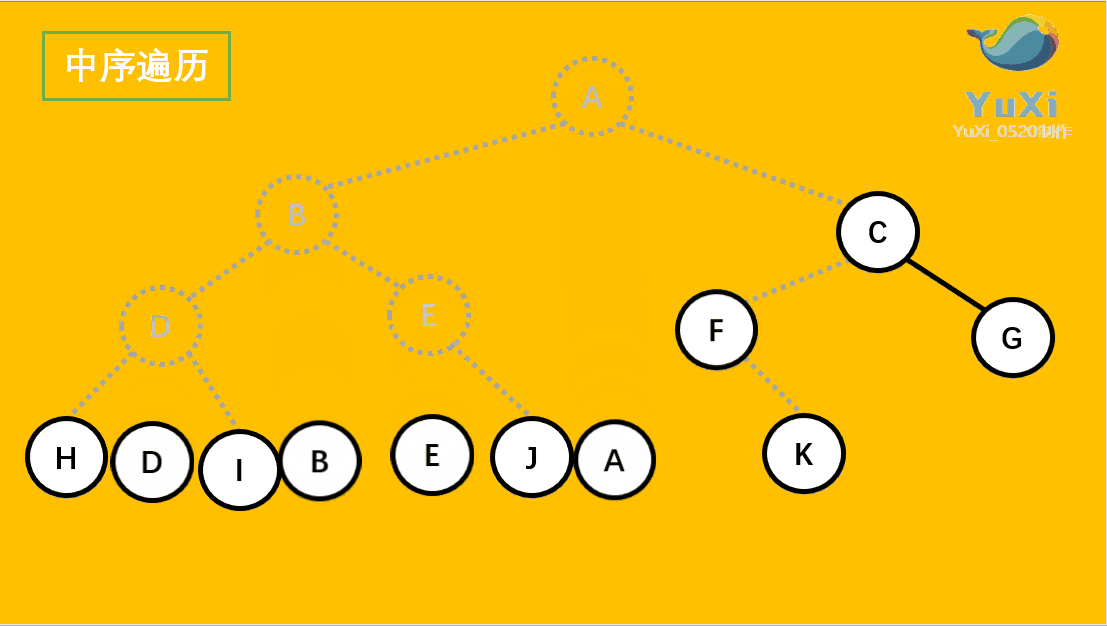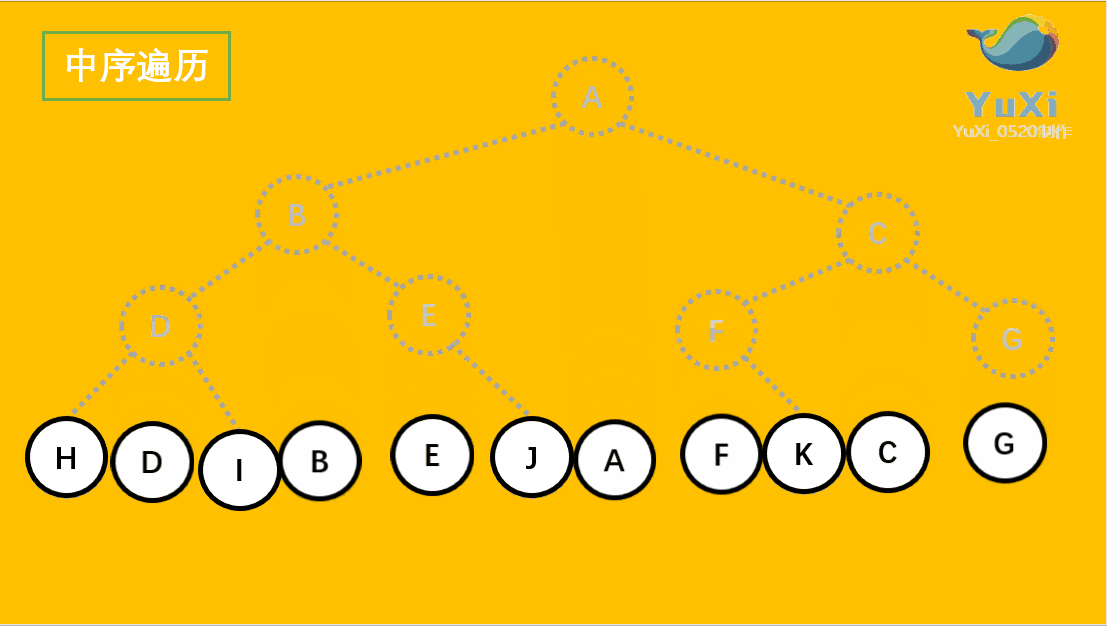
 二叉树三种遍历（动态图+代码深入理解）_二叉树的三种遍历例题带图_杨 戬的博客-CSDN博客

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root) 
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	BinaryTreeInOrder(root->left);
	printf("%d ", root->data);
	BinaryTreeInOrder(root->right);
}

🍟后序遍历

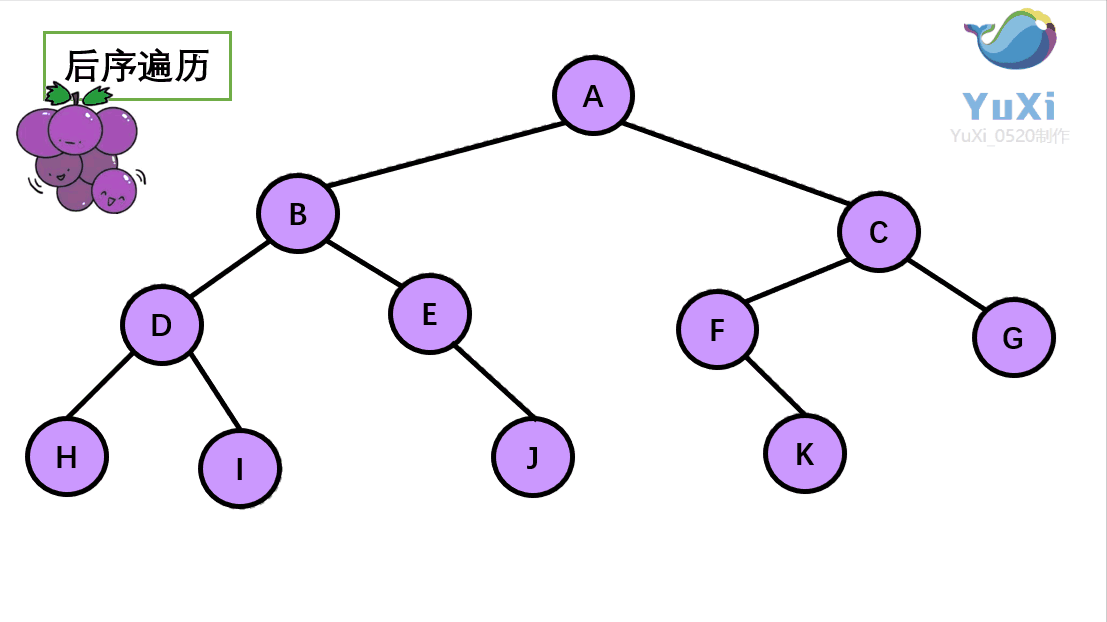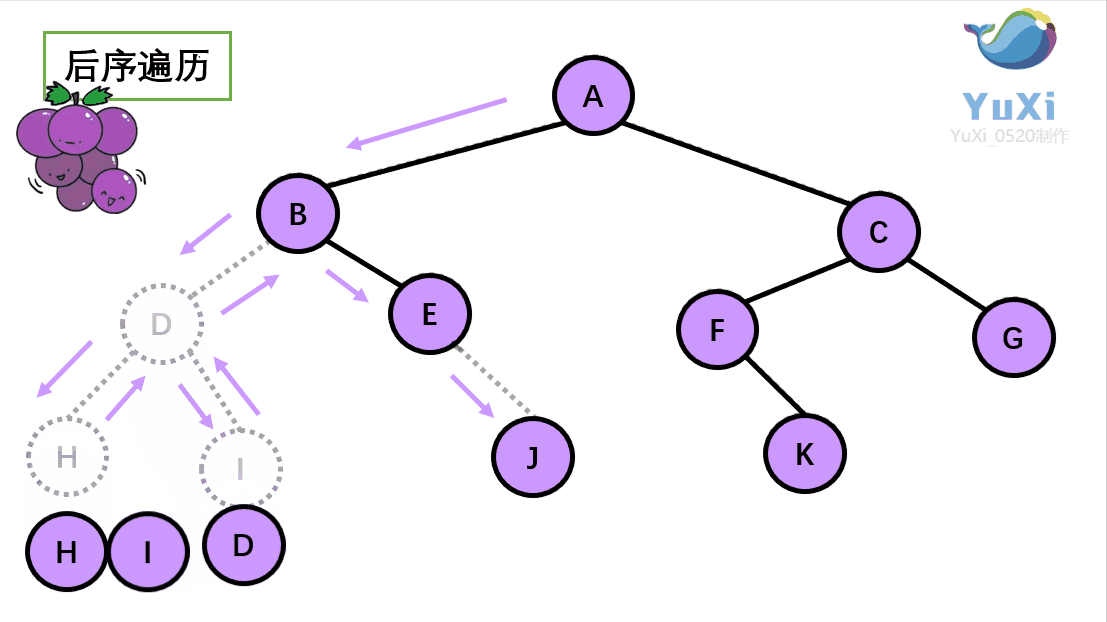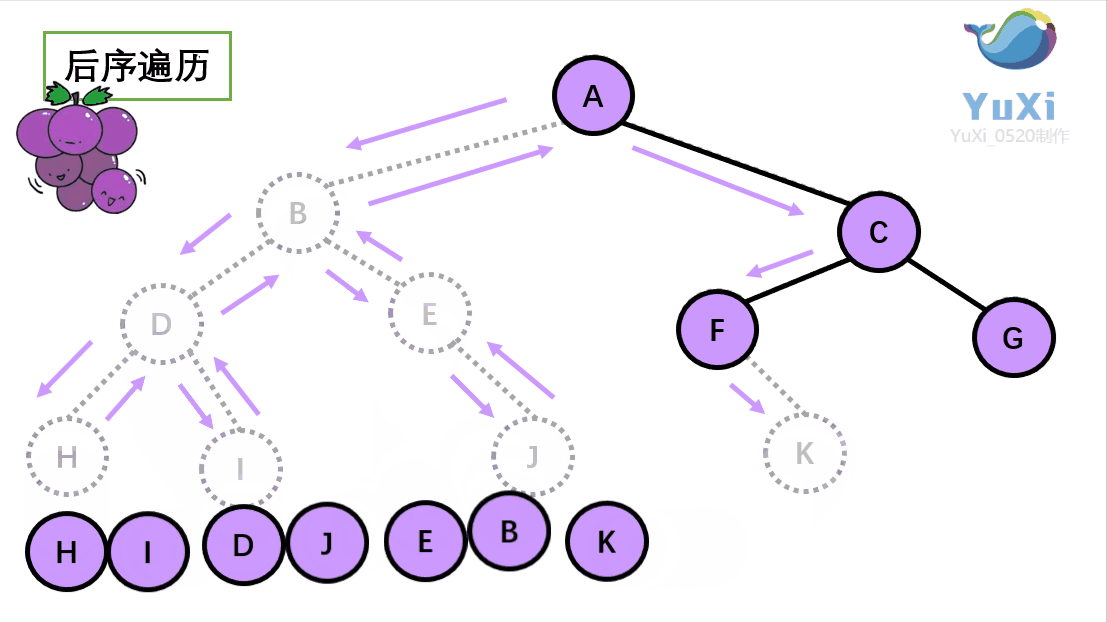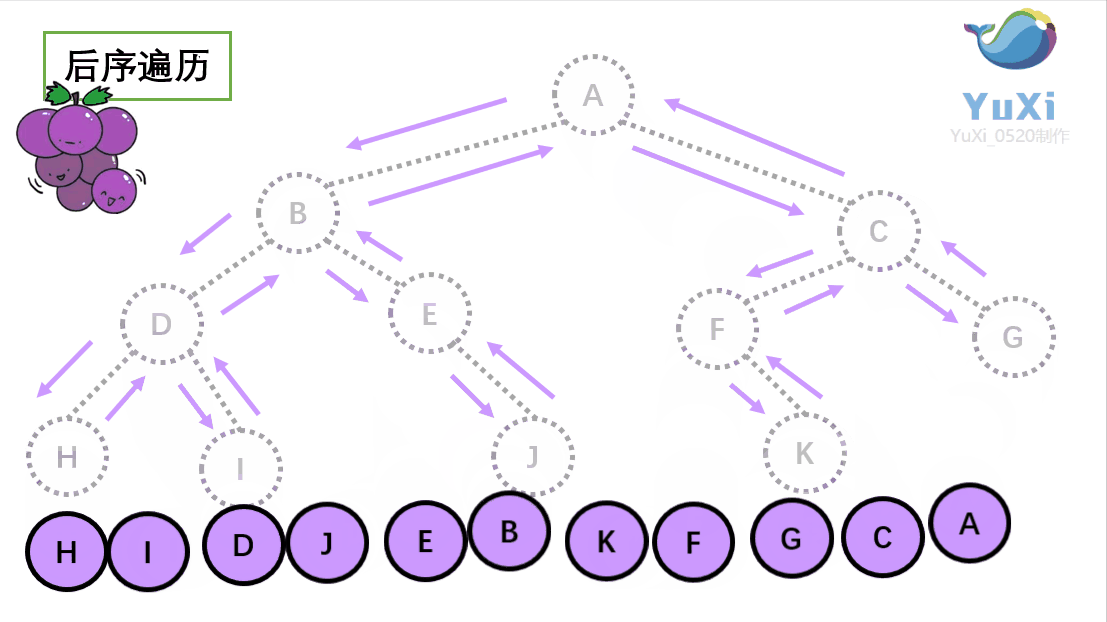
       🚩 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。（左子树——右子树——根）

 二叉树三种遍历（动态图+代码深入理解）-阿里云开发者社区

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%d ", root->data);
}

 🍟层序遍历

       🚩 层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

🔴层序遍历的思路及代码

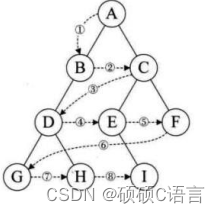
        ⭕层序遍历需要用到队列的一些知大家可以先去了解一下队列的特点队列的概念及结构（内有成型代码可供CV工程师参考）_硕硕C语言的博客-CSDN博客如下图：

      🚨需要注意的是进入队列的不是节点的值，而是节点的地址，这样做可以方便的把后面的左右子树的节点带出来，也方便了后面的判断。 

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;  //建立队列
	QueueInit(&q); //初始化队列
	if (root)  //插入数据
	{
		QueuePush(&q, root);//入队列
	}
	while (!QueueEmpty(&q)) //不为空队列证明后面还有数据没有出来
	{
		BTNode* front = QueueFront(&q); //记录队头的值
		QueuePop(&q); //出队列
		printf("%d ", front->data);
		if (front->left)
			QueuePush(&q, front->left); //遍历左子树
		if (front->right)
			QueuePush(&q, front->right);//遍历右子树
	}
	printf("\n");
	QueueDestroy(&q);//队列的销毁
}

        🥰 这个思想后面的判断二叉树是否是完全二叉树也要用到

🍔 构建二叉树

    🚩构建二叉树的时候要先来引用一道牛客网的题目 二叉树遍历_牛客题霸_牛客网 (nowcoder.com)这个是它的链接可以试着去做一下

✅ 题目要求：

        编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

🥝 示例：

输入：abc##de#g##f###                   

输出：c b e g d f a

 🍟示例的实际图应该是下图这样的一颗树

🥰解题思路：  这个题目要我们构造一个链式二叉树，在先序遍历的过程中构建每一个节点。

 😍代码：

#include <stdio.h>
#include <malloc.h>

typedef struct BTNode
{
    char _data;
    struct BTNode* _left;
    struct BTNode* _right;
}BTNode;

//中序遍历
void Inorder(BTNode* root)
{
    if(root)
    {
        Inorder(root->_left);
        printf("%c ", root->_data);
        Inorder(root->_right);
    }
}

BTNode* CreatBTree(char* str, int* pi)
{
    if(str[*pi]!= '#')
    {
        //当前节点非空，则创建当前节点
        BTNode*root=(BTNode*)malloc(sizeof(BTNode));
        root->_data = str[*pi];
        //字符位置向后移动一个位置
        ++(*pi);
        //创建左子树
        root->_left=CreatBTree(str,pi);
        //字符位置向后移动一个位置
        ++(*pi);
        //创建右子树
        root->_right=CreatBTree(str,pi);
        return root;
    }
    else
        return NULL;  //如果是空节点，则返回NULL
}

int main()
{
    char str[101];
    int i = 0;
    //读入字符串
    scanf("%s", str);
    //创建二叉树
    BTNode* root = CreatBTree(str, &i);
    //中序打印二叉树
    Inorder(root);
    printf("\n");
    return 0;
}

🍔二叉树销毁

😍代码：  

// 二叉树销毁—递归实现
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)  
	{
		return;
	}
	BinaryTreeDestory(root->right);  
	BinaryTreeDestory(root->left);
	free(root);
}

        ✅运用后序遍历（因为如果先释放根节点的话就不能直接找到左右子树了）来实现递归二叉树销毁，结束标志是遇见空节点返回上一级。

🍔二叉树节点个数

😍代码：

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return(BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1);
}

        ✅运用递归（前序）简化了问题，即：二叉树节点个数 = 左子树节点数 + 右子树节点数 + 1 

        ✅递归结束条件是遇到空节点返回 0。

🍔二叉树叶子节点个数

😍代码：

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

🍎叶子节点的概念：度为0的节点称为叶节点

        🍟运用递归（前序）简化了问题，即：二叉树叶子节点个数 = 左子树叶子节点个数 + 右子树叶子节点个数 

       🍟递归结束条件是遇到空节点返回 0， 该节点的左子树节点为空 并且 右子树节点为空，则该节点为叶子节点，返回1。

🍔二叉树第k层节点个数

😍代码： 

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0); //k的值不能为负数
	if (k == 1 && root)  //第k层的判断条件
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

🍎层的概念：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

        🍟不满足第k层的判断条件的不计数,（继续递归下去），当满足第K层的条件的就返回1（返回上一级的函数中）

🍔二叉树查找值为x的节点

😍代码：

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* ret1 = BinaryTreeFind(root->left, x);
	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret1)
		return ret1;
	if (ret2)
		return ret2;
	return NULL;
}

        ✅运用递归（前序）简化了问题，即：二叉树中等于X的节点个数 = 左子树等于X的节点个数 + 右子树等于X的节点个数 

        ✅等于空，或者等于这个要找的值为这里的结束条件，返回的是值等于X的节点指针。这里用了两个临时变量来储存左右两边的个数，这样做可以在返回的时候直接返回，不用再一次的计算。🥰

🍔判断二叉树是否是完全二叉树

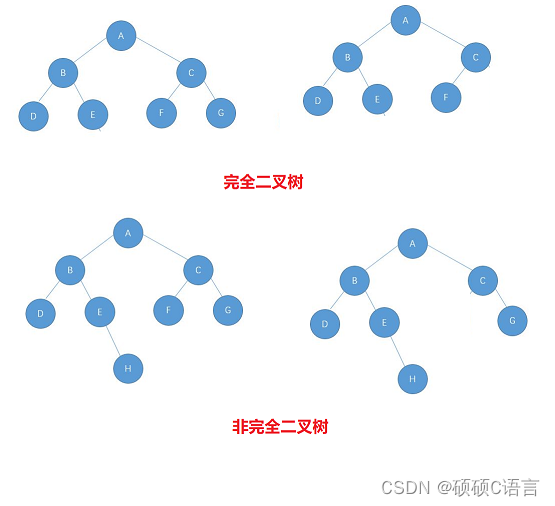
     🍁完全二叉树的概念：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

        ✅运用前面层序遍历的思想用队列进行层序遍历，与它不一样的地方在于这次空值也要入队列，只要队列的队头为空指针就停止操作，看后面是否都为空，由于完全二叉树的自身特性决定了它的后面如果都为空则是完全二叉树，否则不是。

😍代码：

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)   // 遇到空就跳出
			break;
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	// 检查后面的节点有没有非空
	// 有非空，不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

😍二叉树的链式结构所有代码汇总😍

✅BinaryTree.c

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}
//二叉树创建
BTNode* CreatBTree(char* str, int* pi)
{
    if(str[*pi]!= '#')
    {
        //当前节点非空，则创建当前节点
        BTNode*root=(BTNode*)malloc(sizeof(BTNode));
        root->_data = str[*pi];
        //字符位置向后移动一个位置
        ++(*pi);
        //创建左子树
        root->_left=CreatBTree(str,pi);
        //字符位置向后移动一个位置
        ++(*pi);
        //创建右子树
        root->_right=CreatBTree(str,pi);
        return root;
    }
    else
        return NULL;  //如果是空节点，则返回NULL
}

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeDestory(root->right);
	BinaryTreeDestory(root->left);
	free(root);
}

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return(BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1);
}

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);
	if (k == 1 && root)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* ret1 = BinaryTreeFind(root->left, x);
	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret1)
		return ret1;
	if (ret2)
		return ret2;
	return NULL;
}

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root) 
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	BinaryTreeInOrder(root->left);
	printf("%d ", root->data);
	BinaryTreeInOrder(root->right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%d ", root->data);
}

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
	}
	printf("\n");
	QueueDestroy(&q);
}


// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)   // 遇到空就跳出
			break;
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	// 检查后面的节点有没有非空
	// 有非空，不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

 ✅Queue.c

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail\n");
		return;
	}
	newnode->data = x;
	newnode->next = NULL;
	if (pq->ptail == NULL)
	{
		assert(pq->phead == NULL);
		pq->phead = pq->ptail = newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->phead->next == NULL)
	{
		QNode* head = pq->phead;
		free(head);
		pq->phead = pq->ptail = NULL;
		pq->size = 0;
	}
	else
	{
		QNode* head = pq->phead;
		pq->phead = pq->phead->next;
		free(head);
		pq->size--;
	}
}
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return(pq->phead->data);
}
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/607036.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

chatgpt赋能python：Python快捷键：轻松运行你的代码

chatgpt赋能python：Python快捷键：轻松运行你的代码

Python快捷键&#xff1a;轻松运行你的代码 Python是一种广泛使用的编程语言&#xff0c;因为它易于学习、易于使用&#xff0c;并提供了许多强大的库和框架。但是&#xff0c;在日常使用中经常需要重复与代码交互的操作&#xff0c;这可能会降低编程效率。使用Python快捷键可…
阅读更多...
day43:1049. 最后一块石头的重量 II； 474. 一和零； 494.目标和:有多少种方式装满背包

day43:1049. 最后一块石头的重量 II； 474. 一和零； 494.目标和:有多少种方式装满背包

01背包 [1049. 最后一块石头的重量 II (与416分割等和子集类似)](https://leetcode.cn/problems/last-stone-weight-ii/submissions/436837708/)1. dp数组以及下标名义2. 递归公式3. dp数组如何初始化4. 遍历顺序:从后往前遍历5. 代码 494.目标和:有多少种方式装满背包1. dp数组…
阅读更多...
皮卡丘xss之htmlspecialchars、xss之href输出、xss之js输出

皮卡丘xss之htmlspecialchars、xss之href输出、xss之js输出

1.xss之htmlspecialchars htmlspecialchars()函数的功能如下&#xff1a; htmlspecialchars() 函数把预定义的字符转换为 HTML 实体。 预定义的字符是&#xff1a; &#xff08;1&#xff09;& &#xff08;和号&#xff09;成为 &amp; &#xff08;2&#xff09;…
阅读更多...
【编译、链接、装载三】编译器——语法分析、词法分析、语义分析、编译器后端

【编译、链接、装载三】编译器——语法分析、词法分析、语义分析、编译器后端

【编译和链接三】编译器——语法分析、词法分析、语义分析、编译器后端 内容总结一、词法分析&#xff08;Lexical Analysis&#xff09;二、语法分析 &#xff08;Syntactic Analysis, or Parsing&#xff09;三、语义分析&#xff08;Semantic Analysis&#xff09;四、编译器…
阅读更多...
chatgpt赋能python：Python取出元素详解

chatgpt赋能python：Python取出元素详解

Python取出元素详解 在Python编程中&#xff0c;常见到需要取出某个列表、元组或字典中的元素。本文将详细介绍Python如何取出这些元素&#xff0c;并提供相关代码和案例。 取出列表元素 列表是Python编程中最常见的数据结构&#xff0c;下面是列表的定义方式&#xff1a; …
阅读更多...
chatgpt赋能python：Python程序的暂停使用介绍

chatgpt赋能python：Python程序的暂停使用介绍

Python程序的暂停使用介绍 Python是一种高级编程语言&#xff0c;适用于各种应用程序&#xff0c;包括Web开发、数据分析、机器学习等领域。它是一个非常强大的工具&#xff0c;但很多人可能不知道Python是否可以被暂停。在这篇文章中&#xff0c;我们将探讨Python是否可以暂停…
阅读更多...
总结8881

总结8881

学习目标&#xff1a; 月目标&#xff1a;6月&#xff08;线性代数强化9讲2遍&#xff0c;背诵15篇短文&#xff0c;考研核心词过三遍&#xff09; 周目标&#xff1a;线性代数强化1讲&#xff0c;英语背3篇文章并回诵&#xff0c;检测 每日必复习&#xff08;5分钟&#xff…
阅读更多...
MySQL数据库基础（基础命令详解）

MySQL数据库基础（基础命令详解）

1、数据库操作 1.1、显示当前的数据库 SHOW DATABASES; 1.2、创建数据库 CREATE DATABASE IF NOT EXISTS 库名&#xff1b; 1.3、使用数据库 USE 库名; 1.4、删除数据库 DROP DATABASE IF EXISTS 库名&#xff1b; 说明&#xff1a;数据库删除之后&#xff0c;内部看不到对应…
阅读更多...
javaNIO -- ByteBuffer 原理机制

javaNIO -- ByteBuffer 原理机制

说明 author blog.jellyfishmix.com / JellyfishMIX - githubLICENSE GPL-2.0 概述 ByteBuffer 可以理解为是一个 byte 数组&#xff0c;用于读取与写入。ByteBuffer 通过一些精巧的属性和方法, 更高效地使用内存空间。java NIO 中有 8 种缓冲区: ByteBuffer, CharBuffer, D…
阅读更多...
SpringBoot+MyBatis 搭建项目基本框架

SpringBoot+MyBatis 搭建项目基本框架

参考资料:mall整合SpringBootMyBatis搭建基本骨架 一 背景 做的项目多了&#xff0c;就会发现&#xff0c;每次新项目起步&#xff0c;都是一样的。应该整理一个通用的模板来进行快速启动新项目。 二 使用到的框架简介 1.SpringBoot SpringBoot可以让你快速构建基于Spring…
阅读更多...
【实践经验】Latex 表格列间距调整

【实践经验】Latex 表格列间距调整

目录 背景命令 背景 有时候表格列之间的空白区域很大&#xff0c;超出了页面宽度。这时候如果调整表格列与列之间的间隔&#xff0c;无需调整字体大小就能解决这个问题。 命令 \setlength\tabcolsep{3pt} 注意&#xff0c;需要将以上命令&#xff0c;插入到 \begin{table} …
阅读更多...
【项目总结2023年6月3日记】：总结最近项目

【项目总结2023年6月3日记】：总结最近项目

项目总结&#xff0c;记录一下成长&#xff0c;欢迎大家一起学习&#xff0c;一起交流技术&#xff0c;谢谢支持。 项目&#xff1a;从车多色二维码识别&#xff0c;讲究的就是一个不差&#xff0c;识别的准准的 从车多色二维码识别&#xff0c;讲究的就是一个不差&#xff0c;…
阅读更多...
javaScript蓝桥杯----回文字符串

javaScript蓝桥杯----回文字符串

目录 一、介绍二、准备三、目标四、代码五、完成 一、介绍 有言曰&#xff1a;“回文诗&#xff0c;回复读之&#xff0c;皆歌而成文也”。回文诗&#xff0c;是使用词序回环往复的方式所成的诗&#xff0c;通俗来讲就是正读或者倒读都能成为诗句。历经数代诗人的创新&#xf…
阅读更多...
chatgpt赋能python：Python取值：介绍

chatgpt赋能python：Python取值：介绍

Python取值&#xff1a;介绍 Python是一种非常流行的高级编程语言&#xff0c;适用于各种任务&#xff0c;包括数据科学、机器学习、Web开发和自动化。它被广泛使用&#xff0c;因为它易于学习、易于使用、易于阅读和易于维护。Python中的取值对于程序员来说是一个极其有用的工…
阅读更多...
《商用密码应用与安全性评估》第四章密码应用安全性评估实施要点4.6测评报告编制报送和监督检查

《商用密码应用与安全性评估》第四章密码应用安全性评估实施要点4.6测评报告编制报送和监督检查

目录 测评报告管理要求 测评报告编制 测评报告审核 测评报告批准和签发 测评报告存档 测评报告更正 测评报告作废和销毁 保密要求 测评报告体例 测评相关信息报送 1.基本要求 ①测评报告的备案 ②被测信息系统密码应用数据的采集报送 2.测评信息的采集、报送 1&a…
阅读更多...
RVOS环境搭建-01

RVOS环境搭建-01

RVOS环境搭建-01 背景介绍操作系统的定义操作系统的分类典型的 RTOS 介绍课程系统RVOS简介 Hello WorldQEMU介绍QEMU-virt 地址映射 系统引导引导程序要做哪些事情如何判断当前hart是不是第一个hart?如何初始化栈? 如何在屏幕输出Hello World通过串口输出UART特点UART的物理接…
阅读更多...
无线通信技术

无线通信技术

无线通信网包括面向语言通信的移动电话系统以及面向数据传输的无线局域网和无线广域网。 蜂窝通信系统&#xff1a; 1978年&#xff0c;美国贝尔实验室开发了高级移动电话系统&#xff08;AMPS&#xff09;。 AMPS采用模拟制式的频分双工&#xff08;FDD&#xff09;技术 第…
阅读更多...
mysql数据类型有哪几种

mysql数据类型有哪几种

Mysql支持的多种数据类型主要有&#xff1a;数值数据类型、日期/时间类型、字符串类型。 整数 浮点数&定点数 注&#xff1a;定点数以字符串形式存储&#xff0c;对精度要求高时使用decimal较好&#xff1b;尽量避免对浮点数进行减法和比较运算。 时间/日期类型 字符串类型…
阅读更多...
Temporal.Duration 规范用法

Temporal.Duration 规范用法

后端突然告诉我返回给我的时间用了一个新的规范&#xff0c;我展示的时候突然发现这个规范蛮有意思&#xff0c;算是一个新的规范&#xff0c;展示到页面的时候也思考了很多&#xff0c;记录一下子~&#xff08;注&#xff1a;此 blog 主要目的仅是供自己记录&#xff0c;所以写…
阅读更多...
chatgpt赋能python：Python取出列表中的某个数

chatgpt赋能python：Python取出列表中的某个数

Python取出列表中的某个数 在Python中&#xff0c;列表是一种非常重要的数据类型&#xff0c;它可以用来存储一系列有序的元素。在实际的开发中&#xff0c;经常会需要从列表中取出某个特定的数值&#xff0c;本文将介绍如何在Python中完成这个操作。 1. 使用index方法 Pyth…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023