1049. 最后一块石头的重量 II (与416分割等和子集类似)

为什么尽量让石头分成重量相同的两堆，相撞之后剩下的石头就是最小？
这样理解 两个石子相撞是重量相减得到差的过程 那么取出任意两个石子去碰撞 就可以将较大重量的石子作为正数 较小重量作为负数 则可以将所有石子分成正号堆和负号堆两堆 最终的结果就可以表示为给石头数组中的数字添加正负号来使得形成的计算表达式的绝对值最小 此时这道题就和 目标和 那道题的思路一样了（不同在于最后一块石头的重量是求是否能装满背包（如果装不满最多能装多少） 目标和是求装满背包的方法数）

1. dp数组以及下标名义

dp[j]：容量为j的背包所能装的最大价值。

2. 递归公式

-本题相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。

• 递推公式：max(dp[j], dp[j - nums[i]] + nums[i])入代码片

3. dp数组如何初始化

dp[0] = 0
非零下标：dp数组在推导过程中一定是取价值最大的数，如果题目给的价值都是正整数那么非零下标都初始化为0就可以了，这样才能让dp数组在递推公式的过程中取得最大的价值，而不是被初始值覆盖掉

/ 总和不会大于1501，背包最大只需要其中一半，所以10001大小就可以了
vector<int> dp(1501, 0);

4. 遍历顺序:从后往前遍历

5. 代码

class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        
        int sum = 0;
        for(int i = 0; i < stones.size(); i++) {
            sum += stones[i];
        }
        vector<int>dp(1501, 0);
        for(int i = 0; i < stones.size(); i++) {
            for(int j = sum / 2; j >= stones[i]; j--) {
                dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
            }
        }
        return abs(sum - dp[sum / 2] -  dp[sum / 2]);
    }
};

494.目标和:有多少种方式装满背包

1. dp数组以及下标名义

用sum 表示数组集合所有元素相加的值，left表示正整数集合相加，right表示负数相加；
left + right = sum;
left - right = target;
所以：left = (target + sum) / 2;

dp[j]：装满容量为j的背包有dp[j]种方法

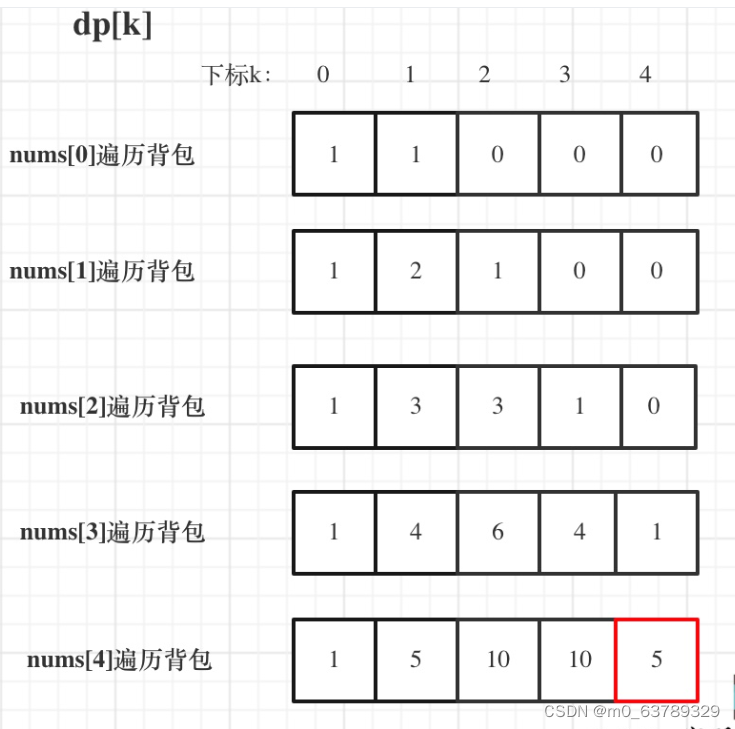
2. 递归公式

例如：dp[j]，j 为5，

已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。11111
已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 容量为5的背包。2111
已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包。311
已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包。41
已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 容量为5的背包。5
dp[5]= dp[4] +dp[3]+ dp[2]+ dp[1]+ dp[0]

• 递推公式：` dp[j] += dp[j - nums[i]]

3. dp数组如何初始化

dp[0] = 1

4. 遍历顺序:从后往前遍历

5. 代码

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for(int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        if(abs(target) > sum) return 0;
        if((sum + target) % 2) return 0;
         vector<int>dp((sum + target) / 2 + 1, 0);
        dp[0] = 1;
        for(int i = 0; i < nums.size(); i++) {
            for(int j = (sum + target) / 2; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[(sum + target) / 2];
    }
};

474. 一和零

**
**

1. dp数组以及下标名义

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

2. 递归公式

dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

3. dp数组如何初始化

dp[0] = 0
非零下标：dp数组在推导过程中一定是取价值最大的数，如果题目给的价值都是正整数那么非零下标都初始化为0就可以了，这样才能让dp数组在递推公式的过程中取得最大的价值，而不是被初始值覆盖掉

/ 总和不会大于1501，背包最大只需要其中一半，所以10001大小就可以了
vector<int> dp(1501, 0);

4. 遍历顺序:从后往前倒序遍历

5. 代码

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
    vector<vector<int>>dp(m + 1,vector<int>(n + 1, 0));
    for(string str: strs) {
        int onenum = 0;
        int zeronum = 0;
        for( char ch : str) {
            if(ch == '0') zeronum++;
            else onenum++;
        }
        for(int i = m ; i >= zeronum; i--) {
            for(int j = n; j >= onenum; j--) {
                dp[i][j] = max(dp[i][j], dp[i - zeronum][j - onenum] + 1);
            }
        }
    }
    return dp[m][n];
    }
};