---

动态规划基础理论

视频连接：动态规划解题方法论大曝光 ！| 理论基础 |力扣刷题总结| 动态规划入门

1.动态规划的五部曲

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 打印dp数组

PS: 先确定递推公式，然后在考虑初始化

---

---

斐波那契数

力扣连接：509. 斐波那契数（简单）

1.动态规划的方法

推导公式：F[n] = F[n-1] + F[n-2];

代码

class Solution {
    public int fib(int n) {

        int[] F = new int[n+1];
        F[0] = 0;  
        if(n==0){
            return F[0];
        }

        F[1] = 1;
        if(n==1){
            return F[1];
        }
       
        for(int i=2;i<=n;i++){
            F[i] = F[i-1] + F[i-2]; //F[n] = F[n-1] + F[n-2];
        }

        return F[n];
    }
}

---

---

爬楼梯

力扣连接：70. 爬楼梯（简单）

dp[0]在此题没有意义。因为没有第0层，故不用初始化

图解步骤

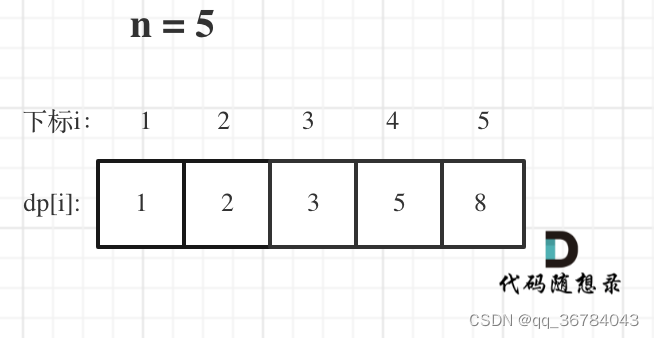
关键点：

确定递推公式，如何可以推出dp[i]呢？

• 从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。

• 首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。

• 还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。

那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！

dp[i] = dp[i - 1] + dp[i - 2]

代码

class Solution {
    public int climbStairs(int n) {
        int[] d = new int[n+1];
        d[1] = 1;
        if(n==1) return d[1];

        d[2] = 2;
        if(n==2) return d[2];
        
        for(int i=3; i<=n; i++){
            d[i] = d[i-1] + d[i-2];
        }

        return d[n];
    }
}

---

---

使用最小花费爬楼梯

力扣连接：746. 使用最小花费爬楼梯（简单）

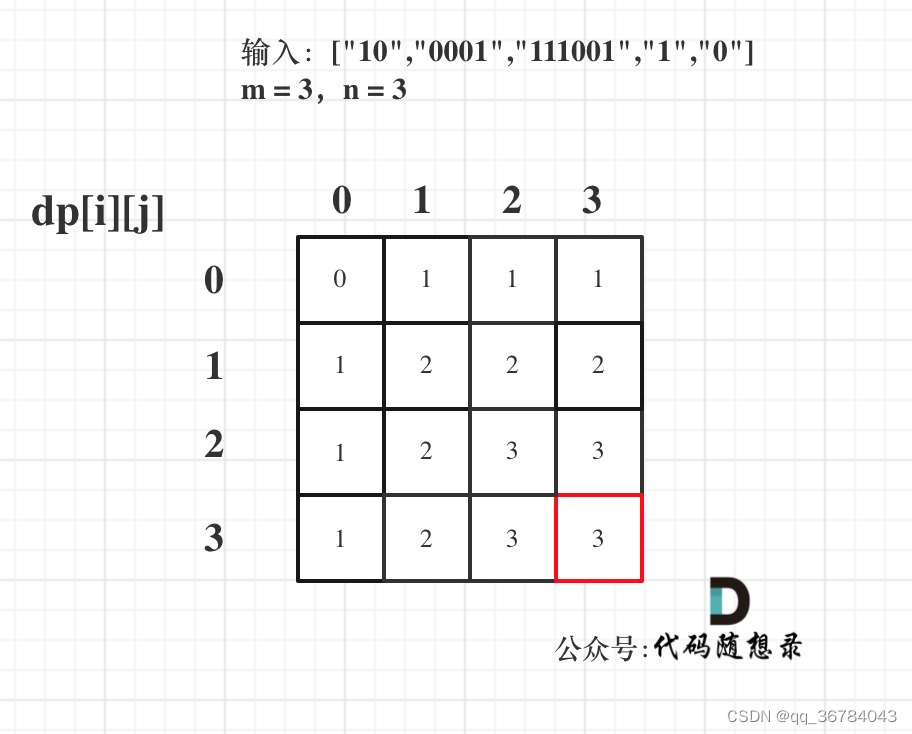
图解步骤

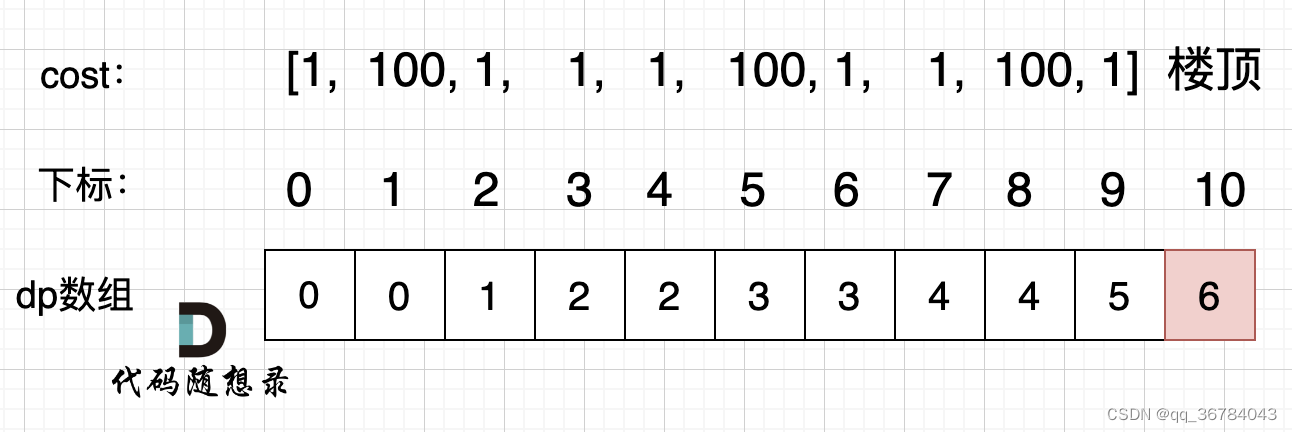
关键点：

• dp数组中设置多一个楼顶的节点记录
• dp[i] = Math.min(dp[i-1], dp[i-2]) + cost[i];

代码

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int step = cost.length;
        int[] dp = new int[step+1];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for(int i=2;i<step;i++){
            dp[i] = Math.min(dp[i-1], dp[i-2]) + cost[i];
        }

        dp[step] = Math.min(dp[step-1], dp[step-2]);

        return dp[step];
    }
}

---

---