---

完全背包

讲解连接：完全背包

1.方法

首先再回顾一下01背包的核心代码

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

我们知道01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。

而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

因为可以重复使用物品

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！

先遍历背包在遍历物品，代码如下：

// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}

图解步骤

遍历物品在外层循环，遍历背包容量在内层循环，状态如图：

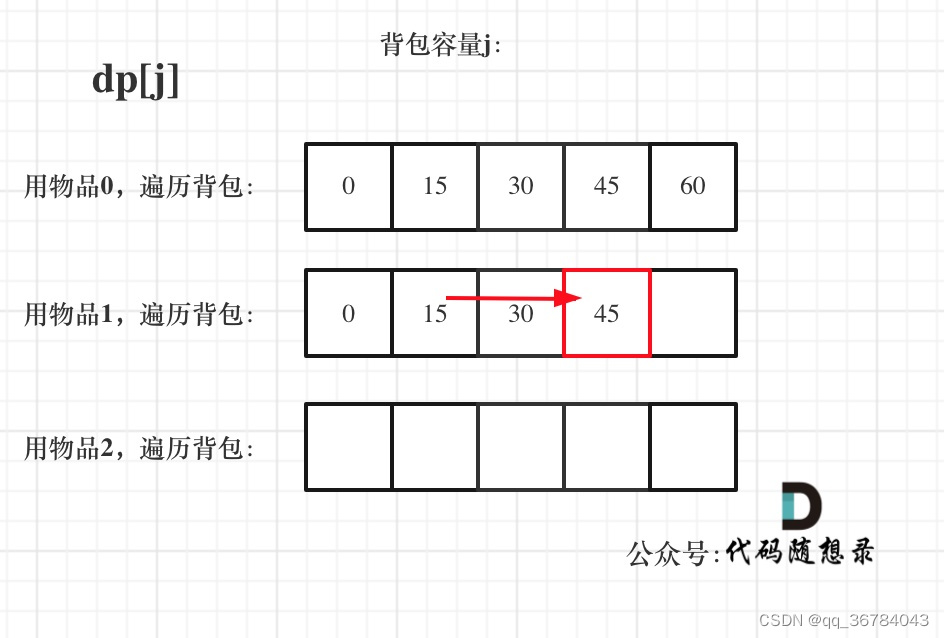
遍历背包容量在外层循环，遍历物品在内层循环，状态如图：

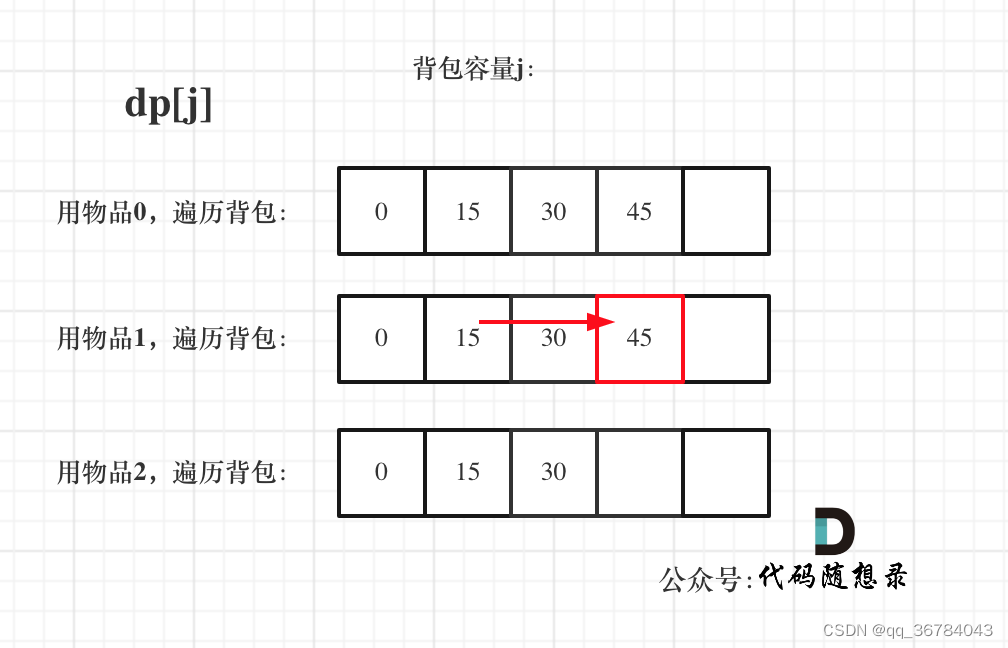
最后，又可以出一道面试题了，就是纯完全背包，要求先用二维dp数组实现，然后再用一维dp数组实现，最后再问，两个for循环的先后是否可以颠倒？为什么？ 这个简单的完全背包问题，估计就可以难住不少候选人了。

---

---

零钱兑换 II

力扣连接：518. 零钱兑换 II（中等）

1.方法

一道典型的背包问题，一看到钱币数量不限，就知道这是一个完全背包。

图解步骤

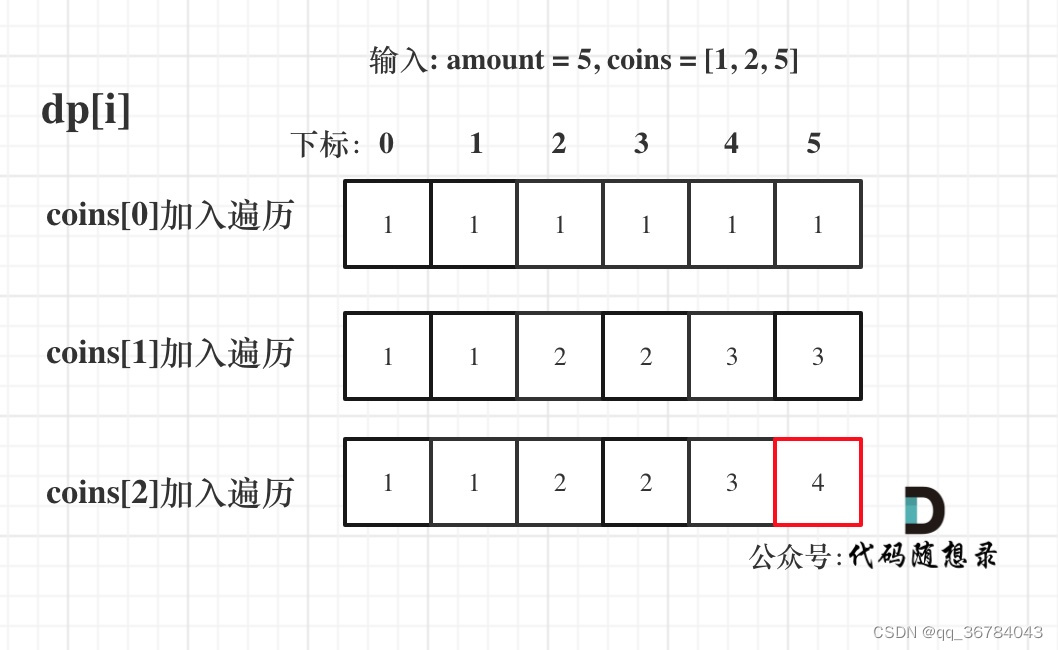
关键点：

在求装满背包有几种方案的时候，遍历顺序是非常关键的。

• 如果求组合数就是外层for循环遍历物品，内层for遍历背包。（无顺序要求）

• 如果求排列数就是外层for遍历背包，内层for循环遍历物品。（有顺序要求）

代码

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount+1];
        dp[0] = 1;
        for(int i=0;i<coins.length;i++){
            for(int j=coins[i];j<=amount;j++){
                dp[j] += dp[j-coins[i]];
            }
        }

        return dp[amount];
    }
}

---

---

组合总和 Ⅳ

力扣连接：377. 组合总和 Ⅳ（中等）

排列数就是外层for遍历背包，内层for循环遍历物品（有顺序要求）

图解步骤

关键点：

• 求装满背包有几种方法，递归公式都是一样的，没有什么差别，但关键在于遍历顺序！

代码

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target+1];
        dp[0] = 1;

        for(int j=0;j<=target;j++){
            for(int i=0;i<nums.length;i++){
                if(j-nums[i]>=0){
                    dp[j] += dp[j-nums[i]];
                }
            }
        }

        return dp[target];
    }
}

---

---