---

整数拆分

力扣连接：343. 整数拆分（中等）

1.动态规划的方法

1. 确定dp数组（dp table）以及下标的含义
   dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

2. 确定递推公式
   其实可以从1遍历j，然后有两种渠道得到dp[i].
   一个是j * (i - j) 直接相乘。
   一个是j * dp[i - j]，相当于是拆分 (i - j) ，对这个拆分不理解的话，可以回想dp数组的定义。
   j * (i - j) 是单纯的把整数拆分为两个数相乘，而 j * dp[i - j] 是拆分成两个以及两个以上的个数相乘。
   递推公式：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});

3. dp的初始化
   只初始化dp[2] = 1，从dp[i]的定义来说，拆分数字2，得到的最大乘积是1

图解步骤

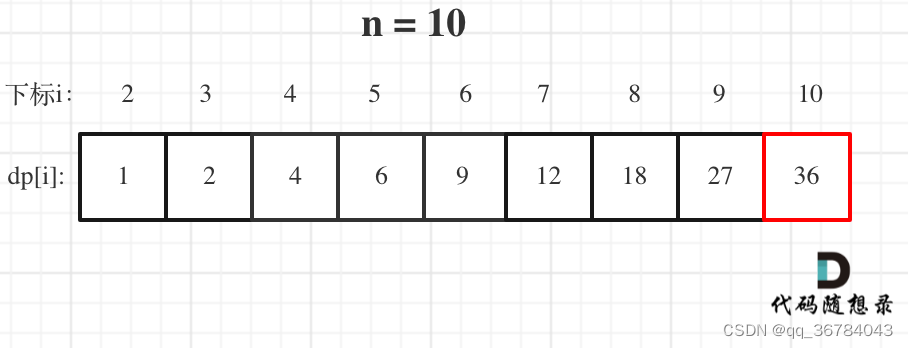
关键点：

• j = i - 1 等价于 j = 1 时的值，故 j < i - 1即可，省略了j = i - 1 这一遍历步
• i是从3开始，这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。

代码

class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n+1];
        dp[2] = 1;
        for(int i=3;i<=n;i++){
            for(int j=1;j<i-1;j++){
                dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
            }    
        }

        return dp[n];
    }
}

---

---

不同的二叉搜索树

力扣连接：96. 不同的二叉搜索树（中等）
视频连接：动态规划找到子状态之间的关系很重要！| LeetCode：96.不同的二叉搜索树

图解步骤

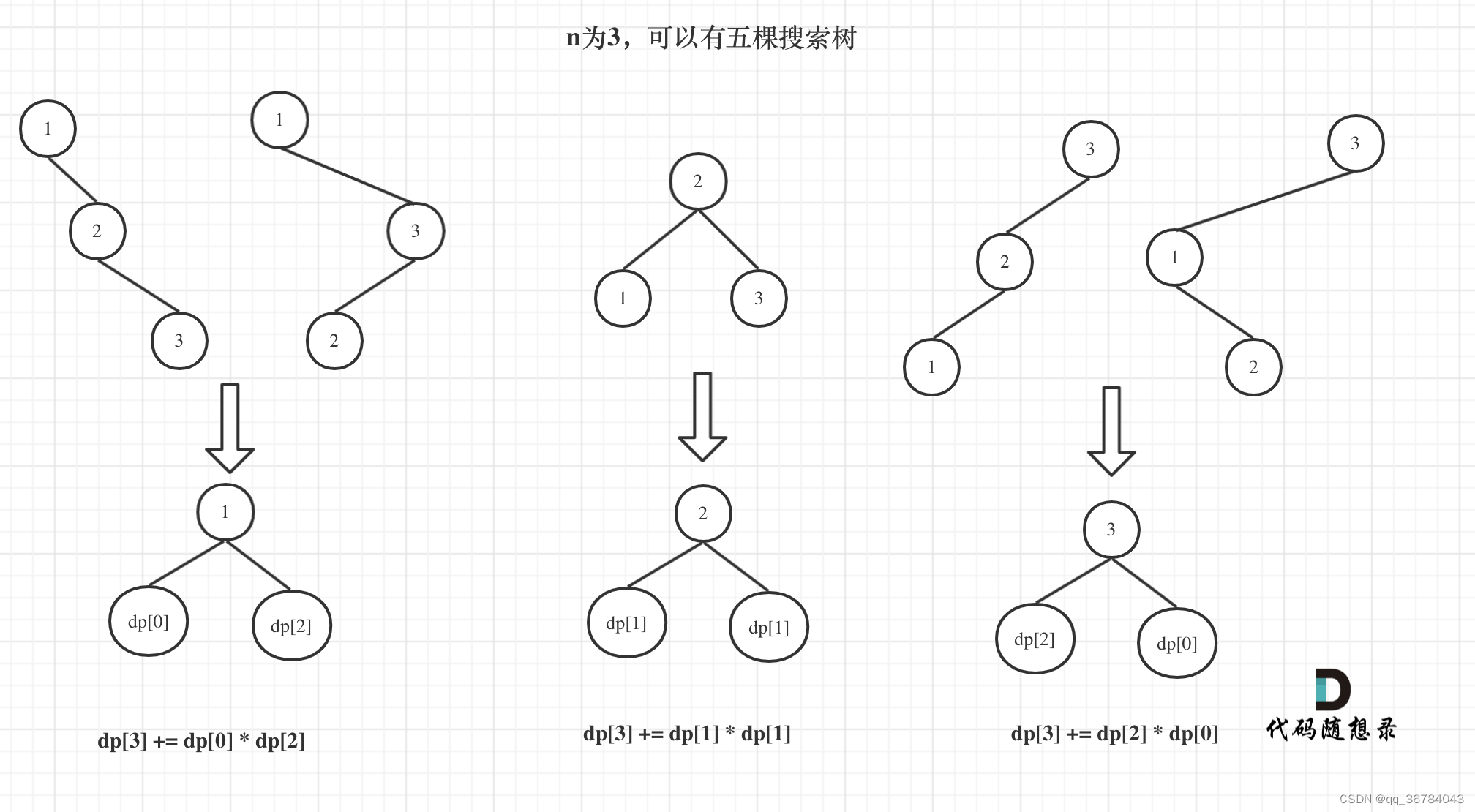
关键点：

• dp含义 dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。
• 递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

代码

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        if(n==1) return dp[1];
        dp[2] = 2;

        for(int i=3; i<=n; i++){
            for(int j=1;j<=i;j++){
                dp[i] += dp[j-1]*dp[i-j];
            }
        }

        return dp[n];
    }
}

---

---