需要源码请点赞关注收藏后评论区留言私信~~~

一、统计分词

统计分词基本逻辑是把每个词语看做由单字组成，利用统计学原理计算连接字在不同文本中出现的次数，以此判断相连字属于特定词语的概率。

二、隐马尔可夫模型

当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态，那么此随机过程通常称之为马尔可夫过程。隐马尔可夫模型（Hidden Markov Model：HMM）是含有隐含且未知参数的马尔可夫过程。

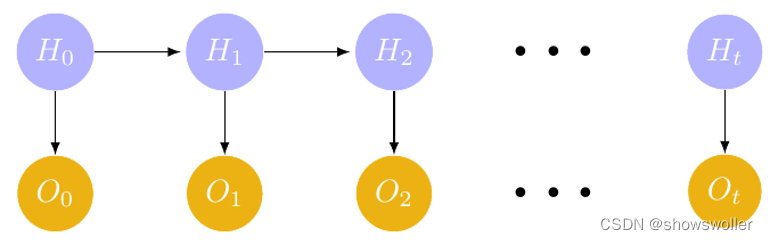
下图表示了隐马尔可夫模型隐藏变量和观测变量相互之间的依赖关系，在任意时刻，观测变量仅仅依赖于隐藏变量，与其他隐藏状态变量和观测变量的取值没有直接关联，同时，特定时刻隐藏状态仅依赖于紧邻上一时刻隐藏状态，与其他状态无关 

三、商务问题描述 

假定某公司销售竞赛指导委员会从n个部门选取员工参加销售业务竞赛，每个部门有m类不同销售能力的员工组成，初始状态下随机选择一个部门后再随机挑选一名职工，职工的类型可以观测，但职工所在的部门为未知信息，第一名员工选择完后，继续按照随机概率选择下一个部门和下一名员工，依次循环知道选择的员工数量满足竞赛人员挑选要求为止

在这个实例中，隐马尔可夫模型可以表示为

1：部门状态信息 n

2：员工的销售能力状态 m

3：从一个部门迁移到另一个部门的转移概率

4：从特定部门选择特定类型的员工概率

5：初始概率分布

隐马尔可夫模型重点解决的问题包括

1：如何确定观测序列的生成概率

2：观测序列已知的前提下 如何优化参数并最大化观测序列的生成概率

3：如何优化隐藏状态序列 从而实现输出期望值观测序列 

四、维特比算法

维特比算法主要用于解决优化隐藏状态序列从而实现输出和期望值观测序列的问题

维特比算法的基本逻辑：

（1）如果最短（或概率最大）路径P经过特定节点G，那么从这条路径起点S到节点G的子路径M，是起点S到节点G之间的最短路径。

（2）从起点S到终点E路径必定经过i时刻的某个状态，如果记录起点S到该状态所有节点的最短路径集合，整体最短路径必经过集合中的某一条。

（3）假定从状态i到状态i+1，起点S到状态i各节点的最短路径已知，计算S到i+1状态的节点的最短路径可以分解为从S到i状态的最短路径，以及从i状态节点到i+1状态节点的最短路径。

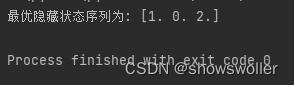
下面是利用维特比算法解决上面的商务问题的结果

由结果可知 最优化的部门选择序列应该是先从第二个部门开始，其次是第一个部门，最后是第三个部门（索引从0开始）

 五、代码

部分代码如下 需要全部代码请点赞关注收藏后评论区留言私信~~

import numpy as np

#维特比算法
def viterbi_algorithm(H, B, rho, O):
	#隐马尔科夫模型隐藏状态数 N=3，总共有三个班级，分别用0,1,2表示
    N = np.shape(H)[0] 
    #观测序列时间序列
    T = np.shape(O)[0]
    
    #特定时刻隐藏状态对应最优状态序列概率 
    mu = np.zeros((T,N))
    #特定时刻隐藏状态对应最优状态前导序列概率 
    index = np.zeros((T,N))
    
    for t in range(T):
        if 0 == t:
            mu[t] = np.multiply(rho.reshape((1, N)), np.array(B[:,O[t]]).reshape((1, N)))
            continue
        for i in range(N):
            temp = np.multiply(np.multiply(mu[t-1], H[:,i]), B[i, O[t]])
            mu[t,i] = max(temp)
            index[t][i] = np.argmax(temp)
    hs = np.zeros((T,))
    t_range = -1 * np.array(sorted(-1*np.arange(T)))
    for t in t_range:
        if T-1 == t:
            hs[t] = np.argmax(mu[t])
        else:
            hs[t] = index[t+1, int(hs[t+1])]
    
    print('最优隐藏状态序列为:', hs)
    return hs
 
def Viterbi_init():
    #H是隐藏状态转移概率分布
 )
    #初始状态概率分布
    rho = np.array([[0.2],
                    [0.4],
                    [0.4]])
    
    #学生的计算机水平观测序列:0-低水平，1-高水平
    O = np.array([[1],
                  [1],
                  [0]]) 
    viterbi_algorithm(H,B,rho,O)
        
if __name__=='__main__':
    Viterbi_init()

 创作不易 觉得有帮助请点赞关注收藏~~~