常用算法-Java

news2024/9/20 5:49:48

基础概念

程序 = 数据结构 + 算法

算法特性：输入、输出、有穷性、确定性、可靠性

算法目标：正确性、可读性、健壮性、运行时间少、内存空间小

时间复杂度

时间复杂度是用来估计算法运行时间的一个单位。

一般来说，时间复杂度高的算法比时间复杂度低的算法慢。

常见时间复杂度(按效率排序)：

        O(1) < O(logn) < O(n) < O(nlogn) < O(n^{2}) < O(n^{2}logn) < O(n^{3})

复杂问题的时间复杂度：

        O(n!) < O(2^{n}) < O(n^{n})

如何快速判断算法复杂度(适用绝大部分简单情况)：

  • 确定问题规模n：循环次数、数组长度、列表长度
  • 循环减半过程：logn
  • k层关于n的循环：n^{k}
  • 复杂过程：根据算法执行过程判断

空间复杂度

空间复杂度是用来评估算法内存占用大小的单位。

空间复杂度的表示方式与时间复杂度完全一样：

  • 算法使用了几个变量：O(1)
  • 算法使用了长度为 n 的一维列表：O(n)
  • 算法使用了 m 行 n 列的二维列表：O(mn)

空间换时间

递归

递归的两个特点：调用自身、结束条件

汉诺塔问题

大梵天创建世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘；大梵天命令婆罗门把圆盘从下面开始按照大小顺序重新摆放在另一个柱子上；规则是：在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘；64个圆盘移动完毕之日，就是世界毁灭之时。

1个盘子：需要1步，2个盘子：需要3步，3个盘子：需要7步；那么 64个盘子：需要 2^{64}-1=18,446,744,073,709,551,615步

假设移动一次需要1s，那么移动 2^{64}-1 次大概需要 5849亿年

public class HanoiTower {
    public static void main(String[] args) {
        function(3, 'A', 'B', 'C');
    }

    public static void function(int n, char a, char b, char c) {
        if (n > 0) {
            function(n-1, a, c, b);
            System.out.println("Moving " + a + " to " + c);
            function(n-1, b, a, c);
        }
    }
}

列表查找

查找：在一些数据元素中，通过一定的方法找出与给定关键字相同的数据元素的过程。

列表查找(线性表查找)：从列表中查找指定元素；        输入：列表、待查找元素；        输出：元素下标(未找到元素一般返回None或-1)；

顺序查找（时间复杂度：O(n)）

也叫线性查找，从列表第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止。内置函数indexOf()。

二分查找（时间复杂度：O(logn)）

循环减半查找，时间复杂度是O(logn)，但是前提是必须先对列表元素进行排序，排序的时间复杂度 > O(n)。

public class BinarySearch {
    public static void main(String[] args) {
        int[] list = new int[]{1,2,3,4,5,6,7,8,9};
        System.out.println(function(list, 3));
    }

    public static int function(int[] list, int val) {
        int left = 0;
        int right = list.length - 1;
        int mid = 0;
        while (left <= right) {//说明候选区还有值
            mid = (left + right) / 2;
            if (list[mid] == val) {
                return mid;
            } else if (mid > val) {//待查找的值在mid左侧
                right = mid - 1;
            } else if (mid < val) {//待查找的值在mid右侧
                left = mid + 1;
            }
        }
        return -1;
    }
}

列表排序

将一组无序的列表变成有序的列表；输入：列表；输出：有序列表；有升序与降序两种排序方式；内置排序函数sort()。

排序Low B三人组

冒泡排序（时间复杂度：O(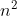n^{2})）

列表每两个相邻的数，如果前面的比后面的大，则交换这两个数；一次排序后，则无序区少一个元素，有序区多一个元素；

代码关键点：趟、无序区范围

冒泡排序优化：如果冒泡排序中的一轮排序没有发生任何位置交换，则说明当前列表已经有序，可以直接结束算法，不需要再循环排序。

public class BubbleSort {
    public static void main(String[] args) {
        int[] list = new int[]{2,5,7,36,6,7,3,33,24,8,9};
        System.out.println(Arrays.toString(function(list)));
    }
    public static int[] function(int[] list) {
        int temp;
        // 外层循环控制比较的轮数
        for (int i = 0; i < list.length-1; i++) {
            // 内层循环控制每轮比较的次数
            boolean exchange = false; // 冒泡排序优化：如果前面几轮已经对整个列表排好顺序，后面不需要再次循环
            for (int j = 0; j < list.length-i-1; j++) {
                if (list[j] > list[j+1]) {//如果前面的数比后面的数大，互换位置
                    temp = list[j];
                    list[j] = list[j+1];
                    list[j+1] = temp;
                    exchange = true; // 冒泡排序优化：如果前面几轮已经对整个列表排好顺序，后面不需要再次循环
                }
            }
            System.out.println(Arrays.toString(list));
            if (!exchange) { // 冒泡排序优化：如果前面几轮已经对整个列表排好顺序，后面不需要再次循环
                return list;
            }
        }
        return list;
    }
}

选择排序（时间复杂度：O(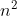n^{2})） 

一轮排序记录最小的数，放到第一个位置；再一轮排序记录无序区列表中最小的数，放到第二个位置。

算法关键点：有序区与无序区、无序区最小数的位置；

public class SelectSort {
    public static void main(String[] args) {
        int[] list = new int[]{8,4,2,3,7,1,6,9,5};
        function(list);
    }
    // 简单选择排序: 循环每次拿到最小的数，然后放在一个新的列表里
    // 缺点：时间复杂度O(n*n),空间复杂度O(2n),所以不推荐使用
    // 优化选择排序：循环每次拿到最小的数，和无序区第一个数交换位置，避免创建新的空间
    public static void function(int[] list) {
        // 外层循环控制比较的轮数
        int temp;
        for (int i = 0; i < list.length-1; i++) {
            // 内层循环控制每轮比较的次数
            int min_index = i;
            for (int j = i+1; j < list.length; j++) {
                if (list[j] < list[min_index]) {
                    min_index = j;
                }
            }
            temp = list[i];
            list[i] = list[min_index];
            list[min_index] = temp;
            System.out.println(Arrays.toString(list)); //打印每次交换的过程
        }
        //System.out.println(Arrays.toString(list));//输出最终排序结果
    }
}

插入排序 （时间复杂度：O(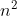n^{2})） 

初始时手里(有序区)只有一张牌(一个元素)，每次摸一张牌(从无序区取一个元素)，插入到手里已有牌的正确位置；

public class InsertSort {
    public static void main(String[] args) {
        int[] list = new int[]{4,2,5,1,6,7,3,9,6,8};
        function(list);
    }
    public static void function(int[] list) {
        int temp, j;
        for (int i = 1; i < list.length; i++) {//摸到牌的下标
            temp = list[i];
            j = i - 1; //j指的是手里牌的下标
            while (j >= 0 && list[j] > temp) {//如果新摸的牌比手里的牌小，手里的牌向右移动
                list[j+1] = list[j];//手里的牌右移一个位置
                j -= 1;//比较的下标前移，下一次跟上一个位置的牌比较
            }
            list[j + 1] = temp;//比较完成后，把摸到的牌放在空出来的位置
            System.out.println(Arrays.toString(list));//输出每次插入的过程
        }
        //System.out.println(Arrays.toString(list));//输出算法结果
    }
}

排序 NB 三人组

快速排序 （时间复杂度：O(nlogn)） 

快速排序思路：

(1) 取一个元素p(第一个元素)，使元素p归位；(2) 列表被p分成两部分，左边都比p小，右边都比p大；(3) 递归完成排序。

public class QuickSort {
    public static void main(String[] args) {
        int[] list = new int[]{5,1,7,2,9,3,8,6,4};
        sort(list, 0, list.length-1);
        System.out.println(Arrays.toString(list));
    }
    // 快速排序算法
    public static void sort(int[] list, int left, int right) {
        if (left < right) {
            int mid = partition(list, left, right);
            //中间数左侧列表取第一个元素p并让其归位，分成两部分，左侧比p小，右侧比p大
            sort(list, left, mid - 1);
            //中间数右侧列表取第一个元素p并让其归位，分成两部分，左侧比p小，右侧比p大
            sort(list, mid + 1, right);
        }
    }
    // 让元素p归位，返回p所在位置索引
    public static int partition(int[] list, int left, int right) {
        int temp = list[left];
        while (left < right) {
            // 从右向左找比temp小的数
            while (left < right && list[right] >= temp) {
                right -= 1; //右边指针向左走一步
            }
            if (left < right) {
                list[left] = list[right];//把右边数移到左边空位上
                left++; //下一轮从左向右：减少一次比较的过程
                System.out.println(Arrays.toString(list));//打印右边数向p左边移动的过程
            }
            // 从左向右找比temp大的数
            while (left < right && list[left] <= temp) {
                left += 1; //左边指针向右走一步
            }
            if (left < right) {
                list[right] = list[left];//把左边数移到右边空位上
                right--; //下一轮从右向左：减少一次比较的过程
                System.out.println(Arrays.toString(list));//打印左边数向p右边移动的过程
            }
        }
        list[left] = temp;
        return left;
    }
}

时间复杂度：每一次归位的时间复杂度是O(n)，需要做logn次归位，所以时间复杂度是O(nlogn);

快速排序的问题：递归消耗系统性能、最坏情况(列表元素正好倒序排列，时间复杂为 O(n^{2}))，针对最坏情况，可取随机位置数作为p；

堆排序（时间复杂度：O(nlogn)） 

树、二叉树、满二叉树、完全二叉树sssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss

树：树是一种可以递归定义的数据结构，比如目录结构；

树是由n个节点组成的集合，1个节点作为根节点，其他节点可以分为m个集合，每个集合本身又是一个子树；

根节点：最顶上的节点；        叶子节点：最底层没有子节点的节点就是叶子节点；

树的深度：从根节点到叶子节点最多有多少层；        树的度：整个树中哪个节点分叉最多，分叉数量就是树的度；

二叉树：树中每个节点最多分两个叉，这种树就是二叉树；

满二叉树：每一层的节点数都达到了最大值，如右图(a)；

完全二叉树：叶子节点只能出现在最下层和次下层，并且最下层的节点都集中在该层最左边的若干位置，如右图(b)；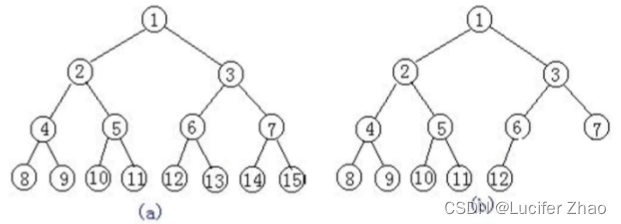

二叉树的存储方式：链式存储方式、顺序存储方式

二叉树的顺序存储方式 sssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss

父节点和左子节点，下标之间有什么关系？

        0-1，1-3，2-5，3-7，4-9

        可以发现有一定规律：i --> 2i+1

父节点和右子节点，下标之间有什么关系？

        0-2，1-4，2-6，3-8，4-10

        可以发现有一定规律：i --> 2i+2

根据子节点下标找父节点下标：(i - 1) / 2取整，假设列表总长为n，那么最后一个子节点下标为 n-1，那么最后一个非叶子节点下标为 (n-2) / 2;

堆：一种特殊的完全二叉树结构

堆排序过程

  1. 建立堆
  2. 得到堆顶元素 ，为最大元素；
  3. 去掉堆顶，将堆的最后一个元素放到堆顶，然后通过一次向下调整重新使堆有序，把去掉的堆顶元素放到最后一个元素位置；
  4. 堆顶元素称为第二个元素；
  5. 重复步骤3，直到堆变空；
public class HeapSort {
    public static void main(String[] args) {
        int[] list = new int[]{9,2,4,6,3,0,5,8,1,7};
        sort(list);
    }
    public static void sort(int[] list) {
        // 建堆：从下往上，从子堆向父堆开始构建
        for (int i = (list.length-2)/2; i > -1; i--) {
            sift(list, i, list.length-1);
        }
        System.out.println(Arrays.toString(list)); //打印建完堆后的列表
        // 挨个出数：把堆顶元素和最后一个元素互换位置，然后从堆顶到倒数第一二元素重新调整结构，变成大根堆，依次重复
        int temp, j;
        for (int i = list.length-1; i > -1; i--) {
            temp = list[0]; //把堆顶元素和堆尾元素互换
            list[0] = list[i];
            list[i] = temp;
            sift(list, 0, i-1); //i-1是新的堆尾
        }
        System.out.println(Arrays.toString(list)); //打印堆排序后的列表
    }
    // 向下调整：保证始终是一个大根堆（父节点元素值比子节点大）
    public static void sift(int[] list, int head, int tail) {
        int i = head; //父节点下标
        int j = 2 * i + 1; //左子节点下标
        int temp = list[i]; //把堆顶存起来
        while (j <= tail) { //避免下标越界
            if (j + 1 <= tail && list[j + 1] > list[j]) { //存在右子节点，且比左子节点大
                j = j + 1; //切换为右子节点
            }
            if (list[j] > temp) { //如果当前子节点比父节点大
                list[i] = list[j]; //将子节点元素存在父节点位置
                // 有可能下一层子节点元素仍然比temp元素大，所以需要继续向下比较，直到最后一个元素
                i = j; //父节点下移一层
                j = 2 * i + 1; //找到新的父节点对应的左子节点
            } else { //如果父节点元素temp更大，把temp就放在原位置，跳出循环
                break;
            }
        }
        list[i] = temp; //不存在子节点，或父节点元素temp比子节点元素大，将此元素放在原位置
    }
}

应用场景：top k问题

现在有 n 个数，设计算法得到前 k 个大的数(k < n)。

解决思路：

  • (1) 堆排序后切片 O(nlogn)；
  • (2) 排序LowB三人组O(nk)；
  • (3) 堆排序优化O(nlogk)；
    • a、取列表前 k 个元素建立一个小根堆，堆顶就是目前第 k 大的数；
    • b、依次向后遍历原列表，如果列表中的元素小于堆顶元素则忽略，否则将堆顶元素替换成列表元素，并对堆进行依次调整；
    • c、遍历列表所有元素后，倒序弹出堆顶；
public class TopK {
    public static void main(String[] args) {
        int[] list = new int[]{9,2,4,8,6,3,7,1,5,10};
        sort(list, 3);
    }
    public static void sort(int[] list, int k) {
        // 1、建堆：取前k个元素建立小根堆
        int[] heap = new int[k];
        for (int i = 0; i < k; i++) {
            heap[i] = list[i];
        }
        // 将 k 个元素构建成小根堆
        for (int i = (k-2)/2; i > -1; i--) {
            siftdown(heap, i, k-1); // i是堆的最后一个非子节点
        }
        // 2、遍历列表后续元素，与小根堆堆顶元素比较
        for (int i = k; i < list.length-1; i++) {
            if (list[i] > heap[0]) { //如果列表后续元素比小根堆中最小的元素还大，那么替换掉堆顶最小元素
                heap[0] = list[i]; //替换堆顶最小元素
                siftdown(heap, 0, k-1); //重新对堆进行调整保证是小根堆
            }
        }
        // 3、小根堆挨个出数进行排序
        int temp;
        for (int i = k-1; i > -1; i--) {
            temp = heap[0];
            heap[0] = heap[i];
            heap[i] = temp;
            siftdown(heap, 0, i-1); //i-1是未排序的最后一个元素下标
        }
        System.out.println(Arrays.toString(heap));
    }
    // 向下调整：构建小根堆
    public static void siftdown(int[] list, int head, int tail) {
        int i = head; //父节点下标
        int j = 2 * i + 1; //左子节点
        int temp = list[i]; //把堆顶元素存起来
        while (j <= tail) { //避免下标越界
            if (j + 1 <= tail && list[j + 1] < list[j]) { //如果右子节点比左子节点小，切换到右子节点上
                j = j+ 1;
            }
            if (list[j] < temp) { //子节点比父节点小
                list[i] = list[j]; //将子节点元素存入父节点位置
                // 有可能还存在下级节点元素比temp小的情况，所以需要继续向下比较，直到最后一个元素
                i = j; //i下标移到下一级
                j = 2 * i + 1;
            } else { //如果父节点元素temp值更小，把temp存在原位置，跳出循环
                break;
            }
        }
        list[i] = temp; //不存在子节点，或父节点元素temp比子节点元素更小，将元素存在原位置
    }
}

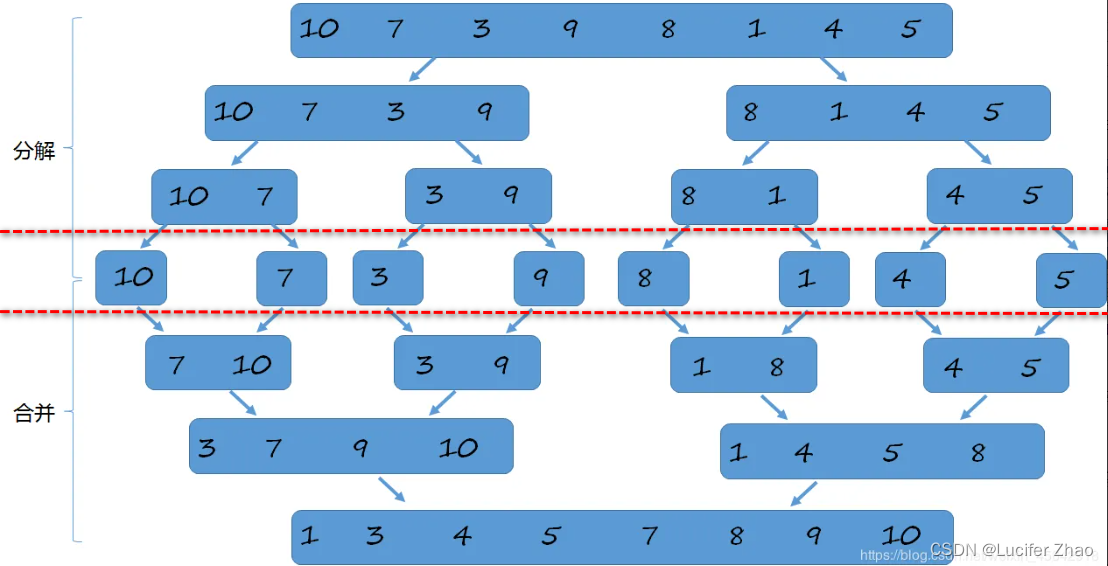
归并排序

归并：假设现在的列表分成两段，两段都有序，将其合成一个有序列表，这种操作就是一次归并；

归并过程：两个下标分别指向两段列表的第一个元素，两个下标所指的元素进行对比，谁小就拿出来放到一个新的列表，然后拿出的元素下标向后移动一位，继续和另一个列表的第一个元素进行对比，直到两个列表所有元素都取出来存入新列表为止；

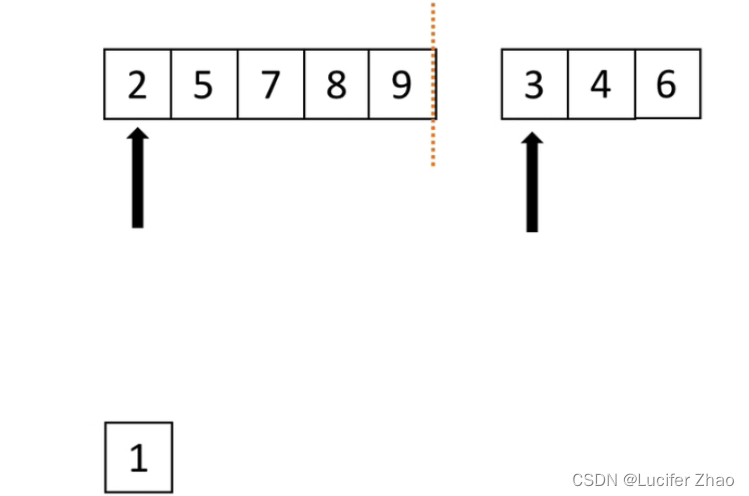
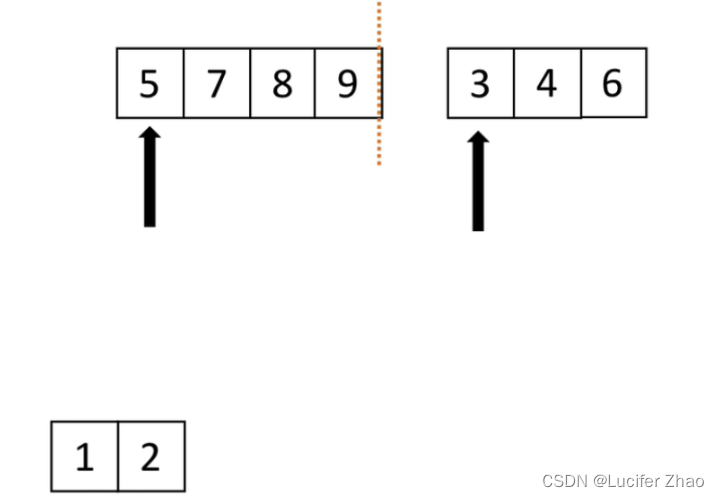
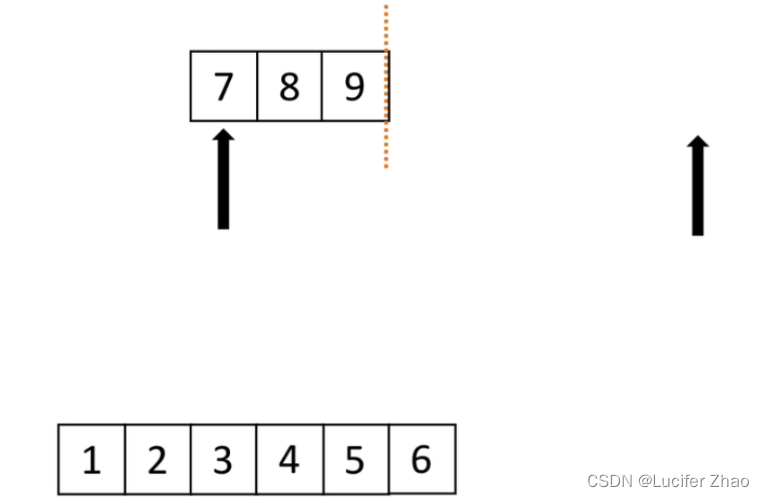
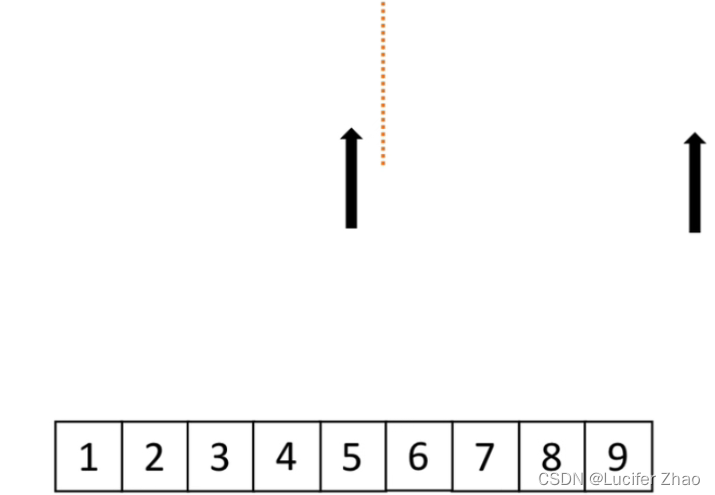
使用归并进行归并排序

  1. 分解：将列表越分越小，直至分成一个元素；
  2. 终止条件：一个元素是有序的；
  3. 合并：将两个有序列表归并，依次归并所有组成新的有序列表；

public class MergeSort {
    public static void main(String[] args) {
        int[] list = new int[]{1,2,5,7,9,3,4,6,8};
        int [] result = sort(list, 0, list.length-1);
        System.out.println(Arrays.toString(result));
        // merge(list, 0, (list.length-1)/2, list.length-1);
    }
    // 归并过程：将一个列表分成两段有序列表，然后合并成一个有序列表
    public static int[] merge(int[] list, int head, int mid, int tail) {
        int i = head; //第一段列表首元素
        int j = mid + 1; //第二段列表首元素
        int[] tempList = new int[tail - head + 1];
        int x = 0;
        while (i <= mid && j <= tail) { //只要两段列表都还有数，进行对比
            if (list[i] < list[j]) {
                tempList[x] = list[i];
                i += 1;
            } else {
                tempList[x] = list[j];
                j += 1;
            }
            x += 1;
        }
        // while执行完，代表有一段列表已经没有元素了
        while (i <= mid) { //代表第一段列表还有元素
            tempList[x] = list[i];
            i += 1;
            x += 1;
        }
        while (j <= tail) { //代表第二段列表还有元素
            tempList[x] = list[j];
            j += 1;
            x += 1;
        }
        System.out.println(Arrays.toString(tempList));
        return tempList;
    }
    // 归并排序
    public static int[] sort(int[] list, int head, int tail) {
        if (head < tail) { //代表还有至少两个元素，递归拆分
            int mid = (head + tail) / 2;
            sort(list, head, mid); //将左边部分排好序
            sort(list, mid+1, tail); //将右边部分排好序
            return merge(list, head, mid, tail); //将两段排好序的列表归并
        }
        return list;
    }
}

希尔排序

计数排序

基数排序

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/60614.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【高并发基础】理解 MVCC 及提炼实现思想

【高并发基础】理解 MVCC 及提炼实现思想

文章目录1. 前言2. MVCC 概念2.1 MVCC 版本链2.2 MVCC trx_id2.3 MVCC Read View3. 提出问题4. 解决问题4.1 不读未提交的数据4.1.1 一般的并发情况4.1.2 特殊的并发情况4.1.3 剩下的并发情况4.2 如果自己修改了数据&#xff0c;要第一时间读到5. MySQL RC 使用 MVCC5.1 MVCC D…
阅读更多...
Git使用学习记录（一、前置知识）

Git使用学习记录（一、前置知识）

Git使用学习记录&#xff08;一、前置知识&#xff09; Git简介 Git 是什么&#xff1f; Git 是目前为止最为先进的分布式版本控制系统&#xff08;分布式版本控制系统没有“中央服务器”&#xff0c;每个⼈的电脑上都是⼀个完整的版本库&#xff0c;⼯作时不需要联网&#xff…
阅读更多...
Dynamics 365 Environment Variables（环境变量）的应用

Dynamics 365 Environment Variables（环境变量）的应用

环境变量这个功能很早就有了&#xff0c;但最近才关注到&#xff0c;是个不错的功能&#xff0c;所以写篇介绍下它的应用。 项目里都会有配置实体这么个东西&#xff0c;用于存储各种常量或者与其他系统集成时的各种配置参数&#xff0c;以往我们都是自定义一个实体用来存放&am…
阅读更多...
PyTorch 2.0发布了，一行代码提速76%

PyTorch 2.0发布了，一行代码提速76%

PyTorch 官方&#xff1a;我们这次的新特性太好用了&#xff0c;所以就直接叫 2.0 了。 前段时间&#xff0c;PyTorch 团队在官方博客宣布 Pytorch 1.13 发布&#xff0c;包含 BetterTransformer 稳定版等多项更新。在体验新特性的同时&#xff0c;不少人也在期待下一个版本的推…
阅读更多...
Mysql进阶学习（十）存储过程和函数流程控制结构

Mysql进阶学习（十）存储过程和函数流程控制结构

Mysql进阶学习&#xff08;十&#xff09;存储过程和函数&流程控制结构存储过程和函数1. 存储过程1.1 创建语法1.2 调用语法1.3 删除存储过程1.4 查看存储过程的信息2. 函数2.1 创建语法2.2 调用语法2.3 查看函数2.4 删除函数3. 存储过程/函数案例4. 流程控制结构4.1. 分支…
阅读更多...
心肺运动试验----各类参数分析笔记

心肺运动试验----各类参数分析笔记

1&#xff1a;定义 什么是心肺运动试验&#xff1f; 心肺运动试验(CPET)是一种可以使研究者同时观察患者的心血管系统和呼吸系统对同一种运动应激的反应情况的临床试验。因为&#xff0c;呼吸道的气体交换与循环相关联&#xff0c;可以同时反映心排血量、肺血流以及外周O2的摄…
阅读更多...
详解设计模式：命令模式

详解设计模式：命令模式

命令模式&#xff08;Command Pattern&#xff09;也被称为行动模式&#xff08;Action Pattern&#xff09;、事物模式&#xff08;Transaction Pattern&#xff09;&#xff0c;是在 GoF 23 种设计模式中定义了的行为型模式。 命令模式 是一种数据驱动的设计模式。请求以命令…
阅读更多...
序列类型（元组（）、列表[]、字符串““）、集合类型（{}、set()）

序列类型（元组（）、列表[]、字符串““）、集合类型（{}、set()）

序列类型 组合数据类型能够将多个同类型或不同类型的数据组织起来 &#xff0c;通过单一的表示使数据操作更有序更容易。根据数据之间的 关系&#xff0c;组合数据类型可以分为三类&#xff1a; 序列类型、集合类型和映射类型。 • 序列类型是一个元素向量&#xff0c;元素之间…
阅读更多...
Centos8安装CDH解决不兼容问题

Centos8安装CDH解决不兼容问题

问题 我的配置 系统&#xff1a; centos8 安装包&#xff1a; CDH-5.16.1-1.cdh5.16.1.p0.3-el7.parcel CDH-5.16.1-1.cdh5.16.1.p0.3-el7.parcel.sha cloudera-manager-centos7-cm5.16.1_x86_64.tar.gz manifest.json 在 http://192.168.1.1:7180/ 上通过web分配percel时分配…
阅读更多...
Python实现基于内容的协同过滤推荐算法构建电影推荐系统

Python实现基于内容的协同过滤推荐算法构建电影推荐系统

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 基于内容(Content Based,CB)的推荐算法&#xff0c;根据用户过去是一段时间内喜欢的物品&#xff0c;由…
阅读更多...
DHTMLX Spreadsheet JavaScript Pro 5.0

DHTMLX Spreadsheet JavaScript Pro 5.0

Spreadsheet — Web-Based Spreadsheet Solution 破解版DHTMLX Spreadsheet is a framework-agnostic JavaScript solution that allows you to quickly add an editable Excel-like spreadsheet on a web page. Unlike online services, DHTMLX Spreadsheet allows you to st…
阅读更多...
Windows x64隐藏可执行内存

Windows x64隐藏可执行内存

文章目录实现效果实现原理VAD内存什么是VAD内存查看VAD内存VAD属性VAD内存可利用的点x64分页机制W7 x64下任意地址PDT PTE算法W10 x64定位随机化页表基址实现隐藏可执行内存隐藏内存对抗实现效果 驱动程序在Test进程中申请一块内存地址并打印&#xff0c;然后控制台程序在接收到…
阅读更多...
Web中的Bias（更新中）

Web中的Bias（更新中）

目录前言数据偏见对人们的影响衡量偏见活跃偏差或少数人的智慧数据偏见其他参考文献前言 本文参考Ricardo Baeza-Yates 2018年发表在《Communications of the ACM》的论文Bias on the Web&#xff0c;论文旨在提高人们对网络使用和内容中存在的偏见对我们所有人造成的潜在影响…
阅读更多...
Methyltetrazine-PEG4-NHS ester,甲基四嗪PEG4琥珀酰亚胺酯

Methyltetrazine-PEG4-NHS ester,甲基四嗪PEG4琥珀酰亚胺酯

一&#xff1a;产品描述 1、名称 英文&#xff1a;Methyltetrazine-PEG4-NHS ester 中文&#xff1a;甲基四嗪-四聚乙二醇-琥珀酰亚胺酯 2、CAS编号&#xff1a;1802907-92-1 3、所属分类&#xff1a;Tetrazine 4、分子量&#xff1a;533.54 5、分子式&#xff1a;C24H3…
阅读更多...
qt单线程实现顺序事件的处理不卡顿技巧（IDE开发）

qt单线程实现顺序事件的处理不卡顿技巧（IDE开发）

需求&#xff1a; 我现在是这样的需求&#xff0c;我正在开发一款嵌入式IDE中&#xff0c;编辑器中光标改变&#xff0c;右侧的符号大纲能对应的改变选中项。 这里的过程是这样的&#xff0c;鼠标位置改变事件函数里&#xff0c;通过光标行号&#xff0c;计算得到当前处于的符…
阅读更多...
通过私钥连接腾讯云，实现免密远程登录

通过私钥连接腾讯云，实现免密远程登录

一、创建 SSH 密钥 系统提示不会保存私钥&#xff0c;要求用户在 10 分钟之内自行下载私钥&#xff0c;要保存在本地电脑和邮箱里面备用。 二、绑定密钥到云服务器 勾选刚才创建的 SSH 密钥&#xff0c;点击上面的绑定云主机&#xff0c;弹窗中要先找到你云主机的地域&#x…
阅读更多...
【计算机毕业设计】74.家教平台系统源码

【计算机毕业设计】74.家教平台系统源码

一、系统截图&#xff08;需要演示视频可以私聊&#xff09; 摘 要 21世纪的今天&#xff0c;随着社会的不断发展与进步&#xff0c;人们对于信息科学化的认识&#xff0c;已由低层次向高层次发展&#xff0c;由原来的感性认识向理性认识提高&#xff0c;管理工作的重要性已逐…
阅读更多...
CentosLinux 6.5安装教程

CentosLinux 6.5安装教程

、开始安装Centos6.5&#xff1a;我们选择“inistall system with basic video driver” 注意&#xff1a;这是一种精简系统的安装模式&#xff1a; 1.安装或升级现有的系统&#xff1b; 2.安装系统并使用基本的显卡驱动&#xff1b; 3.进入系统修复模式&#xff1b; 4.从硬盘…
阅读更多...
[附源码]Python计算机毕业设计SSM竞赛报名管理系统（程序+LW)

[附源码]Python计算机毕业设计SSM竞赛报名管理系统（程序+LW)

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
【计算机毕业设计】基于jsp网上书店（源代码+论文）

【计算机毕业设计】基于jsp网上书店（源代码+论文）

网上书店系统 1.需求分析。 参考设计要求&#xff0c;及可行性的分析&#xff0c;我们确定了如下的需求&#xff1a; 1.数据库设计科学合理。 2.网站主页面简洁美观&#xff0c;可以天蓝色为主色调。 3.网站主页显示各个分类的及总的畅销表、新书榜、推荐榜&#xff0c;显…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023