一、图的基本概念

• 1、基本概念
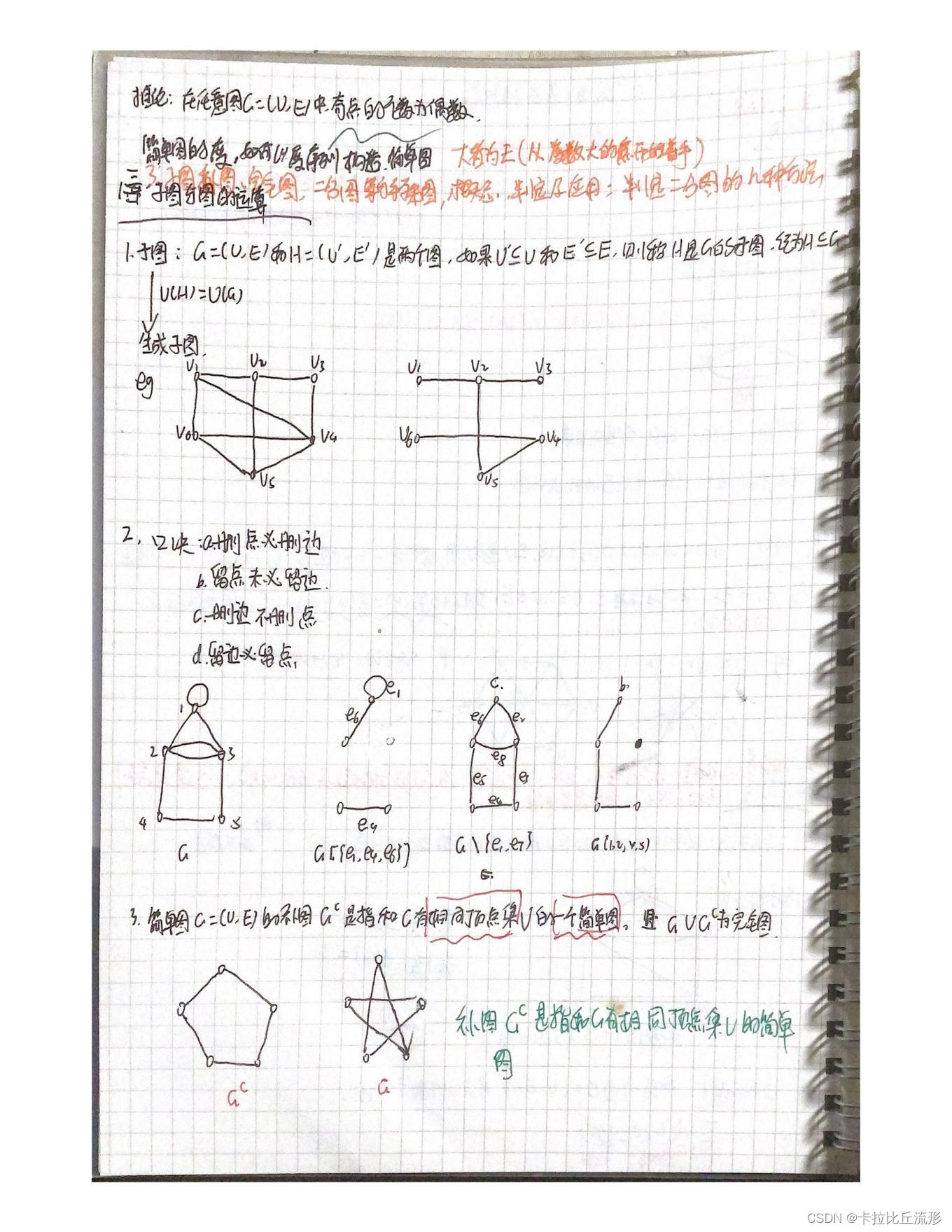
• 2、顶点的度 概念，有关定理及推论（握手定理），度序列的概念及相关结论，根据度序列画图（相互），特别是画简单图。
• 3、子图、补图、完全图、二分图等特殊图，概念、判定 及应用；判断二分图的几种方法。
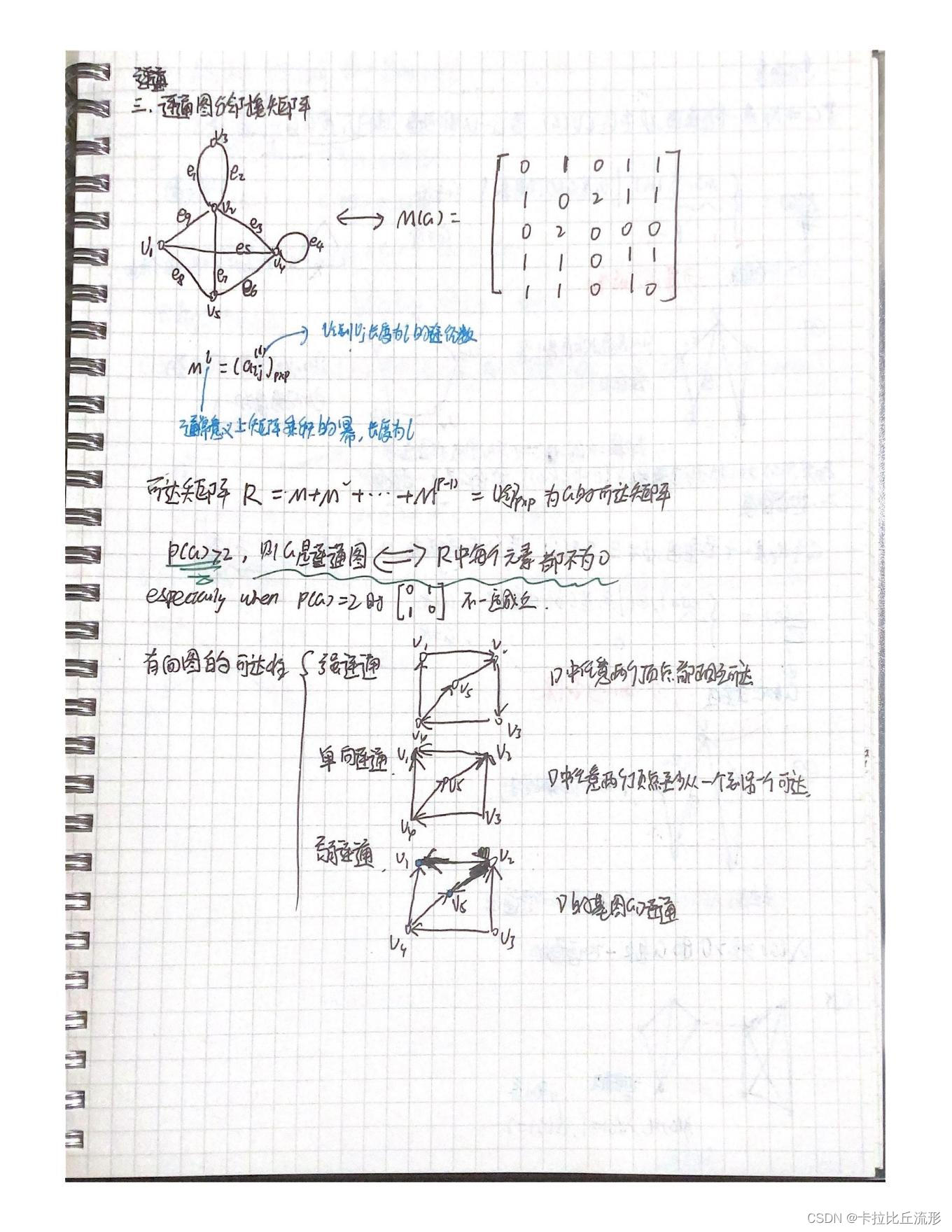
• 4、矩阵表示，邻接矩阵、关联矩阵、度矩阵、其他矩阵；根据图构造矩阵，根据矩阵画图（判断顶点、边）；图的特征多项式、特征值、图的谱。广义邻接矩阵。
• 5、有向图的基本概念，涉及 矩阵表示、连通、树形图、网络流。

二、图的连通性

• 1、概念，如途径、迹、路、圈，图论距离；二分图判定的奇圈法。
• 2、连通，连通分支，连通图的基本性质（如边数的“底线”），连通性与邻接矩阵（可达矩阵）；有向图的连通性。
• 3、点割集、边割集，连通度（点，边）及其与最小度的关系，计算；割边、割点。
• 4、最短路算法，如 Dijkstra 算法（标号法）

三、树

• 1、树的概念、等价命题、树的性质，给定顶点数画树，图的中心点（大营/总部选址）。
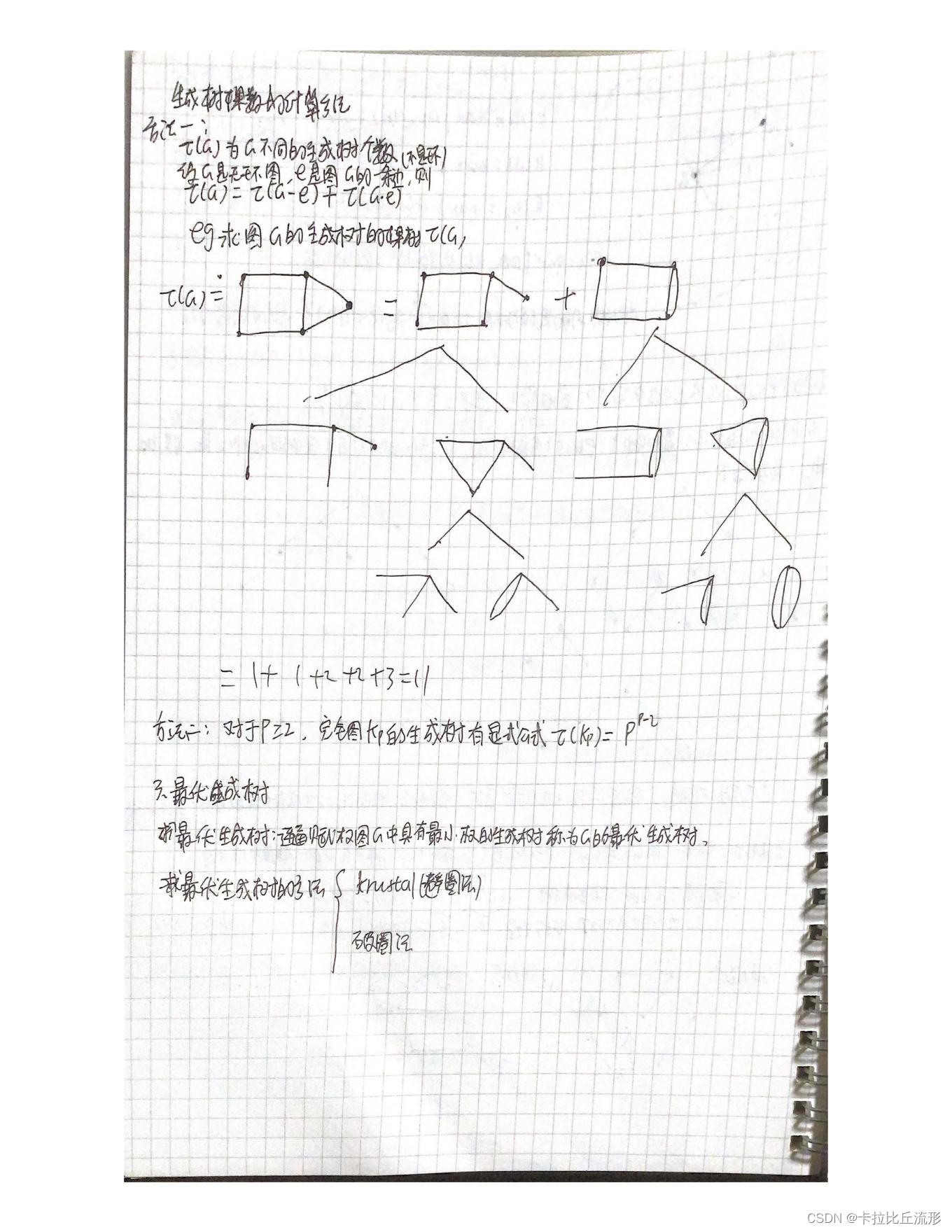
• 2、生成树，概念，构造/寻找生成树的算法（避圈法、破圈法）；生成树棵数的计算（几种方法）。
• 3、最优生成树，构造/寻找的算法
• 4、树形图，基本概念，带权最优二元树的构造算法 及 应用（如最优前缀码）。

四、E 图与 H 图

• 1、基本概念，欧拉迹、欧拉通路、欧拉环游、E 图、M 图，及判定
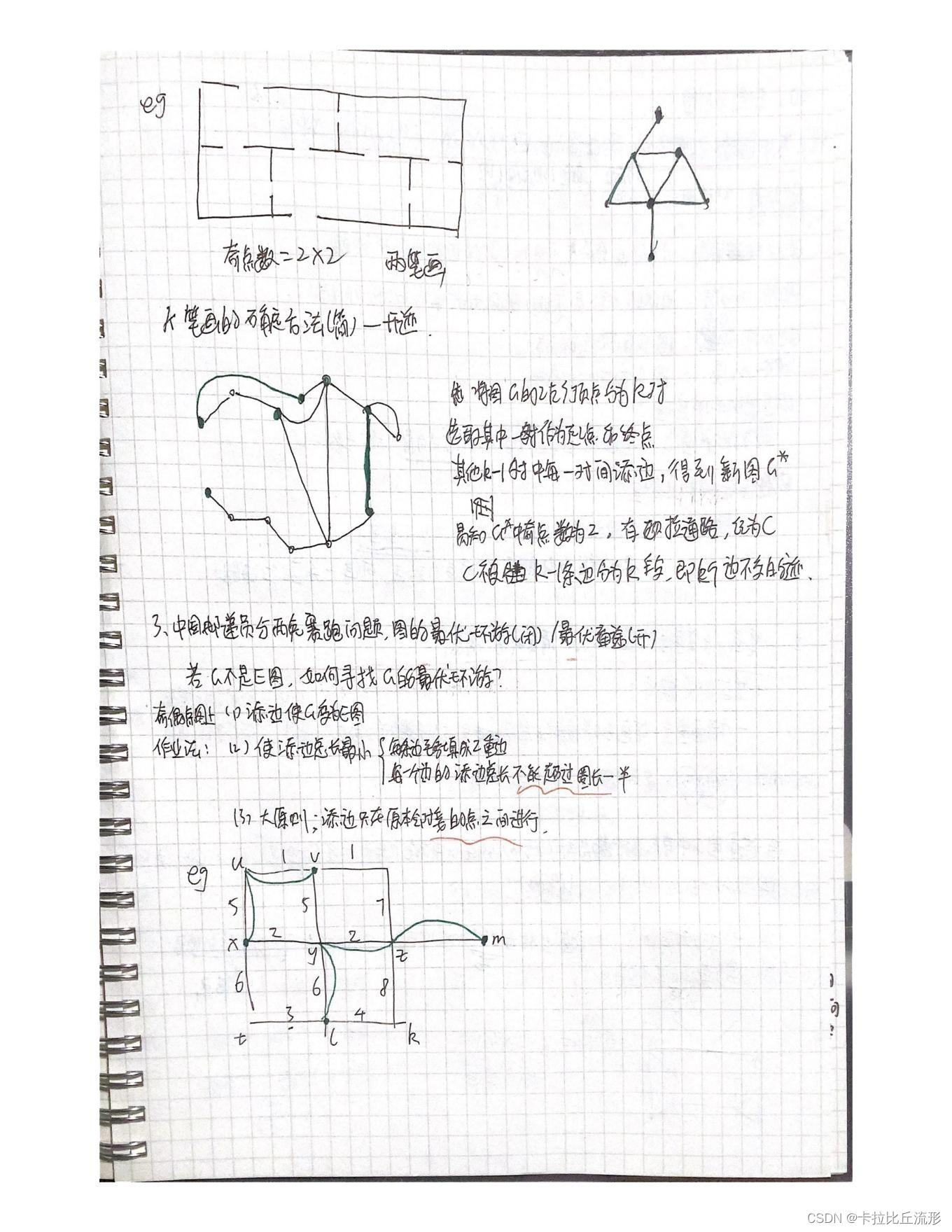
• 2、一笔画/k 笔画 的判定
• 3、中国邮递员与两兔赛跑问题，图的最优环游（闭）/最优通途（开）
• 4、H 图的必要条件（判定不是 H 图），二分图与 H 图的讨论；H 图的充分条件，应用；闭包。

五、对集与独立集

• 1、对集，极大对集，最大对集，完美对集，概念及判定；求（寻找）最大对集（by 关于对集 M 的可扩路, M-augmenting path）；有完美对集的充要条件（H 图与图有完美对集的讨论），二分图的完美对集及拉丁长方的扩充。
• 2、独立集，最大独立集，极大独立集
• 3、覆盖（点覆盖，边覆盖）的概念 *
• 4、Ramsey 数
  六人集会问题/九人集会问题/17 人通信问题 的证明（要求：完全图+鸽巢原理法）
  Ramsey 数及其推广，如 r($S_5$, $S_5$ ) = 7（要求：鸽巢原理法）
  
  
  
  
  
  
  

六、平面图与网络流

• 1、平面图的基本概念、判定；
• 2、网络流的基本概念；
  求网络最大流/最小割算法（by 关于流 f 的可增广路, f-augmenting path）。