4. 有向图的连通性

根据是否考虑边的方向，在有向图中有两种连通性概念：

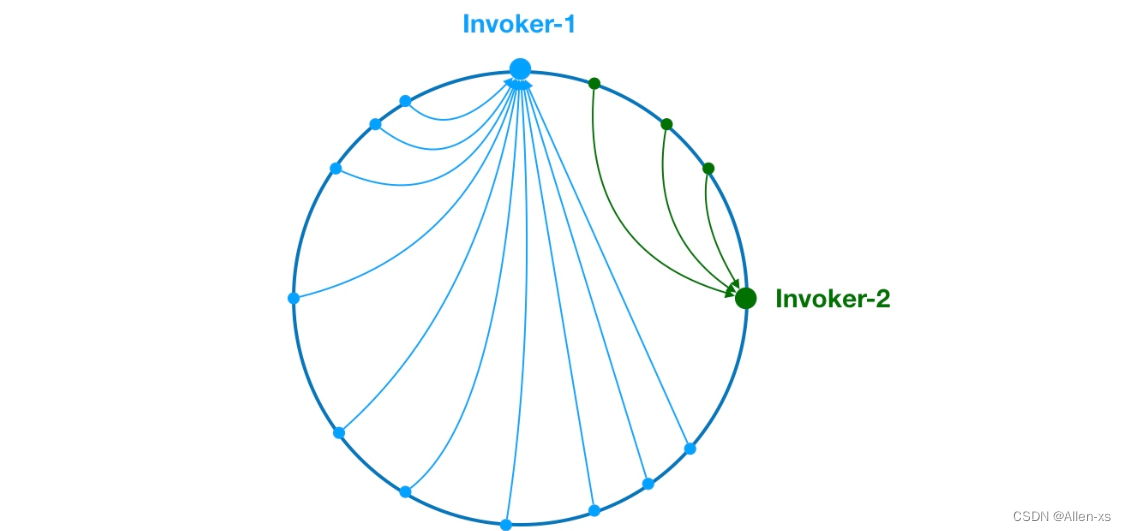
4.1 强连通

强连通的定义：若对于有向图中的任意顶点a和b，都有从 a 到 b 和从 b 到 a 的通路，则该图是强连通的。

4.2 弱连通

弱连通的定义：若在有向图的基本无向图中，任何两个顶点之间都有通路，则该有向图是弱连通的。

注：有向图的基本无向图指的是将原来的有向图去掉方向，得到的图即为这个有向图的基本无向图

4.3 （有向图的）强连通分支

有向图G的子图是强连通的，但不包含在更大的强连通子图中，即极大强连通子图，可称为G的强连通分支 或 强分支。

注意：别忘了单独的一个点也是子图

5. 通路与同构

有多种方式可以利用通路和回路来帮助判定两个图是否同构。
特定长度简单回路的存在，就是一种可以用来证明两个图不同构的有用的不变量。

例题1：
判定图6所示的图G和图H是否是同构的。

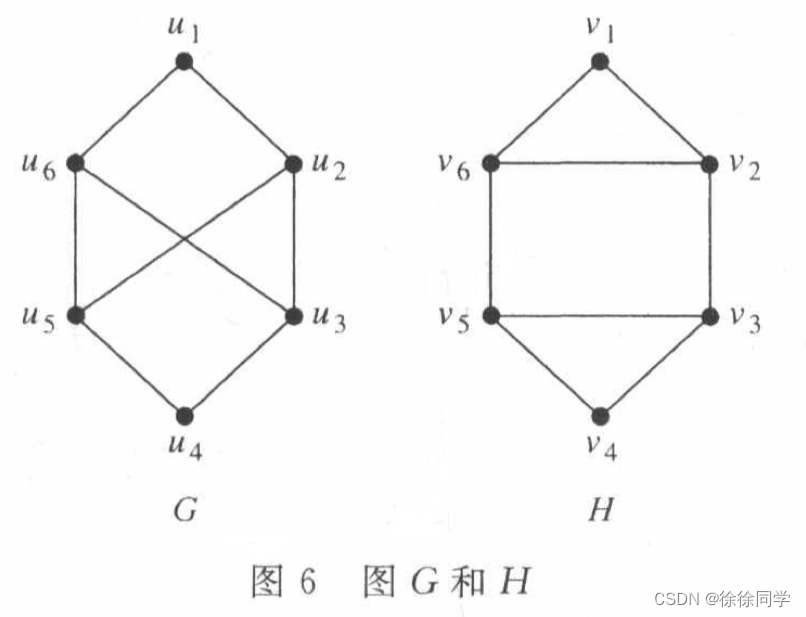
🔴解：图G和图H 不是同构的

G和H都具有6个顶点和8条边。各自具有4个度为3的顶点和2个度为2的顶点。
所以对两个图来说，这3个不变量(顶点数、边数以及顶点度)都是相同的，但是H有长度为3的简单回路，即v₁, v₂, v₆, v₁而通过观察可以看到，G没有长度为3的简单回路(G中的所有简单回路的长度至少为4)

因为存在一条长度为3的简单回路是一个同构不变量，所以G和H是不同构的

例题2：
判定图7所示的图G和图H是否是同构的。

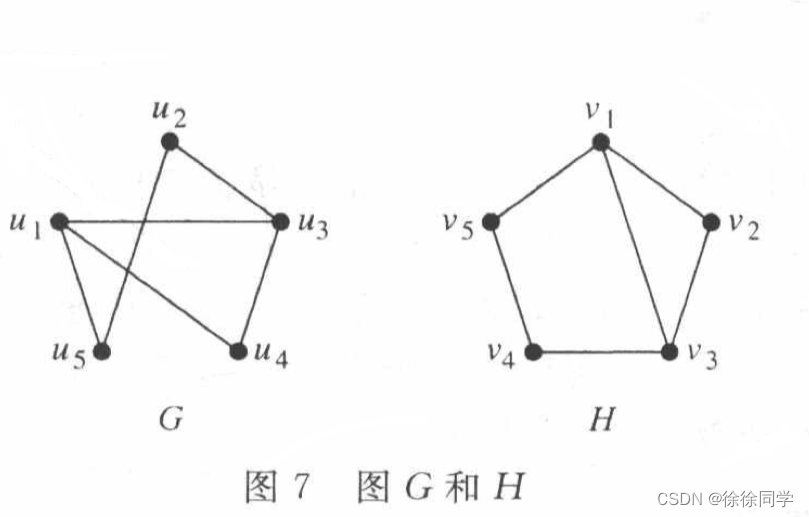
🔴解：图G和图H 是同构的

解G和H都具有5个顶点和6条边，都具有2个度为3的顶点和3个度为2的顶点，而且都具有1个长度为3的简单回路，1个长度为4的简单回路，以及1个长度为5的简单回路。因为所有这些同构不变量都是相同的，所以G和H可能是同构的。

6. 顶点间通路个数的计算

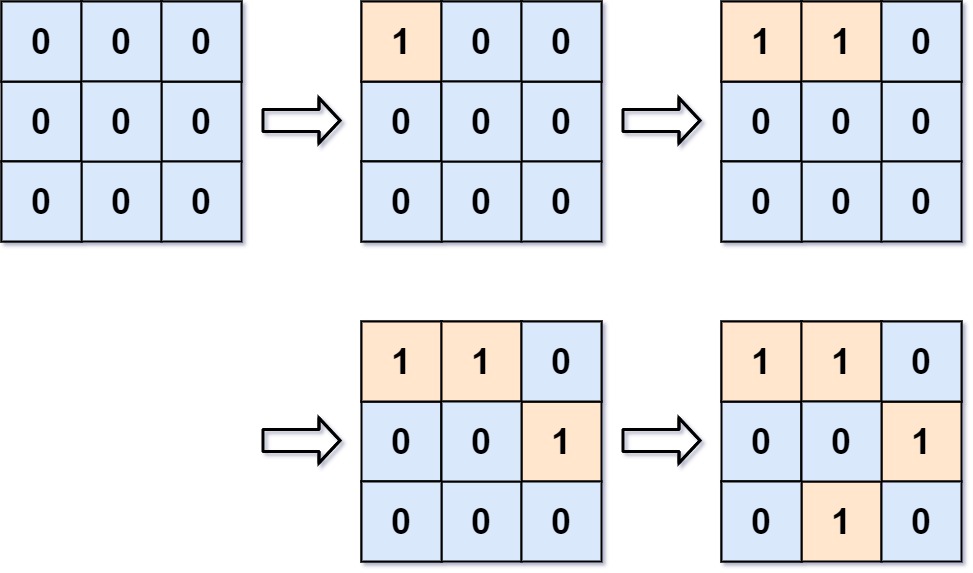
设G是一个图，该图的邻接矩阵A 相对于图中的顶点顺序v₁, v₂, … , v_n (允许带有无向或有向边、带有多重边和环）, 从 v_i 到 v_j 长度为 r 的不同通路的数目等于 A_r 的第 ( i, j) 项，其中 r 是正整数。

求从m到n长度为n的通路的条数，即把邻接矩阵求n次方，再找到对应（m，n）处的数字即为所求