岛屿数量问题2
https://leetcode.cn/problems/number-of-islands-ii/
给你一个大小为 m x n 的二进制网格 grid 。网格表示一个地图,其中,0 表示水,1 表示陆地。最初,grid 中的所有单元格都是水单元格(即,所有单元格都是 0)。
可以通过执行 addLand 操作,将某个位置的水转换成陆地。给你一个数组 positions ,其中 positions[i] = [ri, ci] 是要执行第 i 次操作的位置 (ri, ci) 。
返回一个整数数组 answer ,其中 answer[i] 是将单元格 (ri, ci) 转换为陆地后,地图中岛屿的数量。
岛屿 的定义是被「水」包围的「陆地」,通过水平方向或者垂直方向上相邻的陆地连接而成。你可以假设地图网格的四边均被无边无际的「水」所包围。
示例 1:
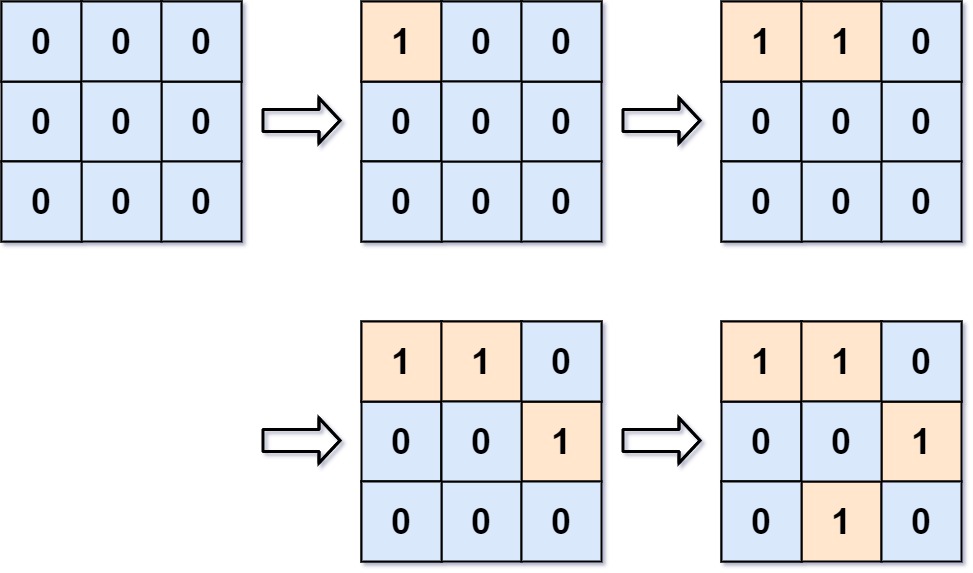
输入:m = 3, n = 3, positions = [[0,0],[0,1],[1,2],[2,1]]
输出:[1,1,2,3]
解释:
起初,二维网格 grid 被全部注入「水」。(0 代表「水」,1 代表「陆地」)
- 操作 #1:addLand(0, 0) 将 grid[0][0] 的水变为陆地。此时存在 1 个岛屿。
- 操作 #2:addLand(0, 1) 将 grid[0][1] 的水变为陆地。此时存在 1 个岛屿。
- 操作 #3:addLand(1, 2) 将 grid[1][2] 的水变为陆地。此时存在 2 个岛屿。
- 操作 #4:addLand(2, 1) 将 grid[2][1] 的水变为陆地。此时存在 3 个岛屿。
示例 2:
输入:m = 1, n = 1, positions = [[0,0]]
输出:[1]
提示:
1 <= m, n, positions.length <= 1041 <= m * n <= 104positions[i].length == 20 <= ri < m0 <= ci < n
理解题目
根据 public static List numIslands21(int m, int n, int[] [] positions) {},其中m指的是二维数组的行,n指的是二维数组的列,二维数组positions指的是传入的1的节点坐标。
举个例子:m = 2,n=3,positions = {{0,0},{0,2},{1,1},{1,2}},指的是在两行三列的二维数组中的{0,0},{0,2},{1,1},{1,2}位置都是1,其他位置都是0。注意这里的坐标顺序是打乱的,出现的顺序也是打乱的。
最重要的一点是:当你遍历到{0,2}位置的时候,后面没便利到的{1,1},{1,2}位置就当是0,遍历到的{0,0}位置是1.所以你可以简单的想象为遍历到哪哪就出现一个1.
思路
1:我打算用并查集的方法,但是这里的1都是随机出现的,所以我们没法一上来就进行father数组与size数组的初始化(怎样的初始化如下)
public UnionFind2(char[][] board) {
//行数
int H = board.length;
//列数
int L = board[0].length;
this.L = L;
fatehr = new int[H * L];
size = new int[H * L];
help = new int[H * L];
sets = 0;
//遍历一遍board二维数组。
for (int i = 0; i < H; i++) {
for (int j = 0; j < L; j++) {
//只有二维数组board是’1‘的,一维数组才会放入数。
//这样一维数组就会有很多位置是空的,但是这不重要。
if (board[i][j] == '1') {
//将二维数组下标转化为一维数组的下标。
int k = index(i, j);
fatehr[k] = k;
size[k] = 1;
sets++;
}
}
}
}
我们需要动态的初始化,就是说遇到谁就初始化谁的father与size。
2:我知道合并的时候,如果两个数可以合并,那么一定会伴随着sets–,以及size[small] = 0。集合的数量一定会减少,并且small祖先的集合数清零。但在这里我们用size[k] != 0来表示节点是岛屿,size[k] == 0来表示节点是水。所以当集合合并后不可以直接清零,保持不动即可。方便新出节点判别当前节点是岛屿。
package algorithmbasic.class16;
// https://leetcode.cn/problems/number-of-islands-ii/
import java.util.ArrayList;
import java.util.List;
public class numIslands2 {
public static List<Integer> numIslands21(int m, int n, int[][] positions) {
//对并查集进行初始化操作,创建好一维数组father,size,以及辅助数组help。设置记录集合数量的变量sets。
UnionFind1 unionFind1 = new UnionFind1(m, n);
List<Integer> ans = new ArrayList<>();
for (int[] p : positions) {// -------------------------- 二维数组遍历的新方法。
ans.add(unionFind1.connect(p[0], p[1]));
}
return ans;
}
/**
* 并查集内部类。
*/
public static class UnionFind1 {
/**
* 属性
*/
static int[] father;
static int[] size;
static int[] help;
static int sets;
//列的长度大小
static int L;
//行的长度大小
static int H;
/**
* 构造器
* 这里我们没有一上来就直接进行初始化操作,我们需要走一步看一步。
*/
public UnionFind1(int m, int n) {
father = new int[m * n];
size = new int[m * n];
help = new int[m * n];
sets = 0;
L = n;
H = m;
}
/**
* index方法
* 传入二维数组的行列参数:i,j 找到对应的一维数组的下标 k
* 公式:K = i * positions[0].length + j
*/
public static int index(int i, int j) {
return i * L + j;
}
/**
* findAncestor方法
* 传入一个节点,然后从这个节点开始一直往上找,直到直到最上边为止,返回最上面的节点。
*/
public static int findAncestor(int cur) {
int j = 0;
while (cur != father[cur]) {
//进行优化,将途径的节点进行记录。
help[j++] = cur;
cur = father[cur];
}
//cur == father[cur]
j--;
while (j >= 0) {
father[help[j--]] = cur;
}
return cur;
}
/**
* union合并方法
* 将 i,j m,n两个位置所在的集合进行合并
*/
public static void union(int i, int j, int m, int n) {
//防止越界条件
if (m < 0 || m >= H || n < 0 || n >= L) {
return;
}
//根据二维数组的下标找到一维数组的下标。
int i1 = index(i, j);
int i2 = index(m, n);
//只有都是岛屿时才可以合并。
if (size[i1] != 0 && size[i2] != 0) {
//找到各自节点的祖先节点。
int fatherA = findAncestor(i1);
int fatherB = findAncestor(i2);
//只有祖先不同时才可以合并,防止祖先相同时反复合并,反复的sets--,导致数据不准确。
if (fatherA != fatherB) {
//找到祖先节点fatherA所在集合大小sizeA。
int sizeA = size[fatherA];
//找到祖先节点fatherB所在集合大小sizeB。
int sizeB = size[fatherB];
//big指向集合数量较多的祖先节点。
int big = sizeA > sizeB ? fatherA : fatherB;
//small指向集合数量较少的祖先节点。
int small = big == fatherA ? fatherB : fatherA;
//进行合并
//注意这个地方size[small]不要被置为0.
father[small] = big;
size[big] = size[big] + size[small];
sets--;
}
}
}
/**
* connect连接方法
* 传入两个参数 i,j 说明二维数组positions的 i,j位置出现了1,然后对其进行相连,连接完之后,返回二维数组目前一共有多少集合。
*/
public static int connect(int i, int j) {
int k = index(i, j);
//之前
if (size[k] == 0) {
//初始化当前位置的father与size数组。
size[k] = 1;
father[k] = k;
sets++;
//进行上下左右的合并。
union(i, j, i + 1, j);
union(i, j, i - 1, j);
union(i, j, i, j + 1);
union(i, j, i, j - 1);
}
return sets;
}
}
}
时间复杂度
时间复杂度是O(m * n + k),k指的是position数组中1的数量为k。
m*n是初始化并查集的复杂度,因为在构造并查集对象的时候,会为并查集对象的数据结构分配空间并进行初始化操作。
father = new int[m * n]; size = new int[m * n]; help = new int[m * n];时间复杂度都是m*n。
方法二:
方法一讲的如果m*n比较大,会经历很重的初始化,而k比较小,所以采取如下方法,其时间复杂度是O(k)
只需要初始化是1的节点,其他节点不需要初始化。
package algorithmbasic.class16;
// https://leetcode.cn/problems/number-of-islands-ii/
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
/**
* 方法二:时间复杂度是O(K)
* 课上讲的如果m*n比较大,会经历很重的初始化,而k比较小,怎么优化的方法
*/
public class numIslands2_2 {
public static List<Integer> numIslands22(int m, int n, int[][] positions) {
List<Integer> ans = new ArrayList<>();
UnionFind2 unionFind2 = new UnionFind2(m, n);
for (int[] p : positions) {
ans.add(unionFind2.connect(p[0], p[1]));
}
return ans;
}
/**
* 并查集内部类
*/
public static class UnionFind2 {
/**
* 属性
*/
//之前写的并查集我们需要额外建立一个Dot类来区分相同的元素
//其实可以直接用一个String来区分,比如说3行4列 写成 ->"3_4"
static HashMap<String, String> fatherMap;
static HashMap<String, Integer> sizeMap;
static int sets;
//行
static int H;
//列
static int L;
//辅助数组
static ArrayList<String> list;
/**
* 构造器
*/
public UnionFind2(int m, int n) {
fatherMap = new HashMap<>();
sizeMap = new HashMap<>();
list = new ArrayList<>();
sets = 0;
this.H = m;
this.L = n;
}
/**
* findAncestor方法
* 创建一个参数,直至找到他的祖先
*/
public static String findAncestor(String k) {
while (!fatherMap.get(k).equals(k)) {
list.add(k);
k = fatherMap.get(k);
}
// k == fatherMap.get(k).
for (String s : list) {
fatherMap.put(s, k);
}
list.clear();
return k;
}
/**
* union方法
*/
public static void union(String key, String k) {
//如果有传进来的k,就进行合并。
if (fatherMap.containsKey(k)) {
//找到key的祖先fatherA
String fatherA = findAncestor(key);
//找到k的祖先fatherB
String fatherB = findAncestor(k);
//如果两个祖先不一样的就合并。
if (!fatherA.equals(fatherB)) {
//big指向集合比较大的祖先
String big = sizeMap.get(fatherA) > sizeMap.get(fatherB) ? fatherA : fatherB;
String small = big == fatherA ? fatherB : fatherA;
//进行合并
fatherMap.put(small, big);
sizeMap.put(big, sizeMap.get(big) + sizeMap.get(small));
//sizeMap.remove(small);
//这个地方还不能remove,因为有可能其他节点会连接他。
sets--;
}
}
}
/**
* connect方法
* 传入两个参数 i,j 说明二维数组positions的 i,j位置出现了1,然后对其进行相连,连接完之后,返回二维数组目前一共有多少集合。
*/
public static int connect(int i, int j) {
//先判断一下这个坐标之前出现过没,如果之前出现过,说明早已连接好,就跳过
String key = String.valueOf(i) + "_" + String.valueOf(j);
if (!fatherMap.containsKey(key)) {
//进行动态的初始化。
fatherMap.put(key, key);
sizeMap.put(key, 1);
sets++;
//上并进行边界判断
String up = (i - 1 < H && i >= 0) ? String.valueOf(i - 1) + "_" + String.valueOf(j) : null;
if (up != null) union(key, up);
//下
String down = (i + 1 < H && i >= 0) ? String.valueOf(i + 1) + "_" + String.valueOf(j) : null;
if (down != null) union(key, down);
//左
String left = (j - 1 < L && j >= 0) ? String.valueOf(i) + "_" + String.valueOf(j - 1) : null;
if (left != null) union(key, left);
//右
String right = (j + 1 < L && j >= 0) ? String.valueOf(i) + "_" + String.valueOf(j + 1) : null;
if (right != null) union(key, left);
union(key, up);
union(key, down);
union(key, left);
union(key, right);
}
return sets;
}
}
public static void main(String[] args) {
int[][] arr = {{0, 1}, {1, 2}, {2, 1}, {1, 0}, {0, 2}, {0, 0}, {1, 1}};
List<Integer> list = numIslands2_2.numIslands22(3, 3, arr);
System.out.println(list);
}
}