遗传算法：原理与实战

简介

遗传算法是一种模拟达尔文生物进化论的自然选择以及遗传学机制的搜索算法，由 John Holland 在20世纪70年代提出。它们在各种搜索、优化和机器学习任务中已被广泛应用。

遗传算法原理

1. 编码

遗传算法的第一步是将问题的可能解表示为一种称为染色体（或基因）的数据结构。这个过程称为编码。在简单的遗传算法中，这种表示通常是一个二进制字符串，但也可以是其他数据类型，如整数或实数。

2. 初始种群

初始种群由多个随机生成的染色体组成。种群大小是预先设定的，并且可以根据问题的具体需求进行调整。

3. 适应度函数

适应度函数是评估染色体（即解）质量的函数。它取决于我们试图解决的特定问题。适应度函数返回的值（适应度分数）越高，染色体的质量越好。

4. 选择

选择过程旨在从当前种群中选择出将参与产生新解的染色体。一般来说，适应度越高的染色体被选择的概率越大。这样可以保证优良的解得以保留，同时还能保持种群的多样性。

5. 交叉（配对）

交叉是一种模拟生物中的性繁殖的运算。它从两个父染色体中创建一个或两个后代。交叉运算符根据预先设定的交叉概率进行操作。

6. 变异

变异是对新生成的后代进行随机修改的过程，以引入新的特征并保持种群的多样性。变异通过改变染色体的一部分来进行。

7. 迭代

新的种群（即新的解集）现在准备好通过适应度函数进行评估，并进入下一轮的选择、交叉和变异过程。这个过程将持续进行，直到达到预设的停止条件。

遗传算法的应用

遗传算法已经在各种领域找到了广泛的应用，包括但不限于：

优化问题：例如旅行商问题、背包问题、作业调度问题等。
机器学习：遗传算法可以用于特征选择、神经网络训练、超参数优化等。
生物信息学：在基因识别、蛋白质折叠、生物网络设计等方面使用遗传算法。

实战：使用Python和遗传算法解决旅行商问题

旅行商问题（Travelling Salesman Problem，TSP）是一种经典的优化问题，它的目标是找到一条访问所有城市并返回原点的最短路径。

安装相关库

在开始之前，我们需要安装一些必要的Python库。我们将使用DEAP库（Distributed Evolutionary Algorithms in Python）进行遗传算法的实现，matplotlib库进行结果的可视化。

pip install deap matplotlib

代码实现

在开始编写代码之前，我们先导入必要的库：

import random
from deap import creator, base, tools, algorithms
import matplotlib.pyplot as plt

在我们的问题中，染色体可以表示为城市的访问顺序，例如 [0, 1, 2, 3, ..., n-1] 表示先访问第0个城市，然后是第1个城市，以此类推。我们可以随机生成一个初始种群，并定义一个适应度函数来计算路径的总长度。

# 定义城市坐标
CITIES = [
    (60, 200), (180, 200), (80, 180), (140, 180),
    (20, 160), (100, 160), (200, 160), (140, 140),
    (40, 120), (100, 120), (180, 120), (60, 80),
    (120, 80), (180, 80), (20, 40), (100, 40),
    (200, 40), (20, 20), (60, 20), (160, 20)
]

# 定义适应度函数
def distance(individual):
    total = 0
    size = len(individual)
    for i in range(size):
        city1 = CITIES[individual[i]]
        city2 = CITIES[individual[(i+1) % size]]
        total += ((city1[0]-city2[0])**2 + (city1[1]-city2[1])**2)**0.5
    return total,

# 确定问题的目标是最小化或最大化
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin)

toolbox = base.Toolbox()
# Attribute generator
toolbox.register("indices", random.sample, range(len(CITIES)), len(CITIES))
# Structure initializers
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.indices)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# Operator registering
toolbox.register("mate", tools.cxPartialyMatched)
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
toolbox.register("

select", tools.selTournament, tournsize=3)
toolbox.register("evaluate", distance)

def main():
    pop = toolbox.population(n=300)
    hof = tools.HallOfFame(1)
    stats = tools.Statistics(lambda ind: ind.fitness.values)
    stats.register("avg", numpy.mean)
    stats.register("std", numpy.std)
    stats.register("min", numpy.min)
    stats.register("max", numpy.max)

    pop, log = algorithms.eaSimple(pop, toolbox, cxpb=0.7, mutpb=0.2, ngen=40, 
                                   stats=stats, halloffame=hof, verbose=True)
    return pop, log, hof

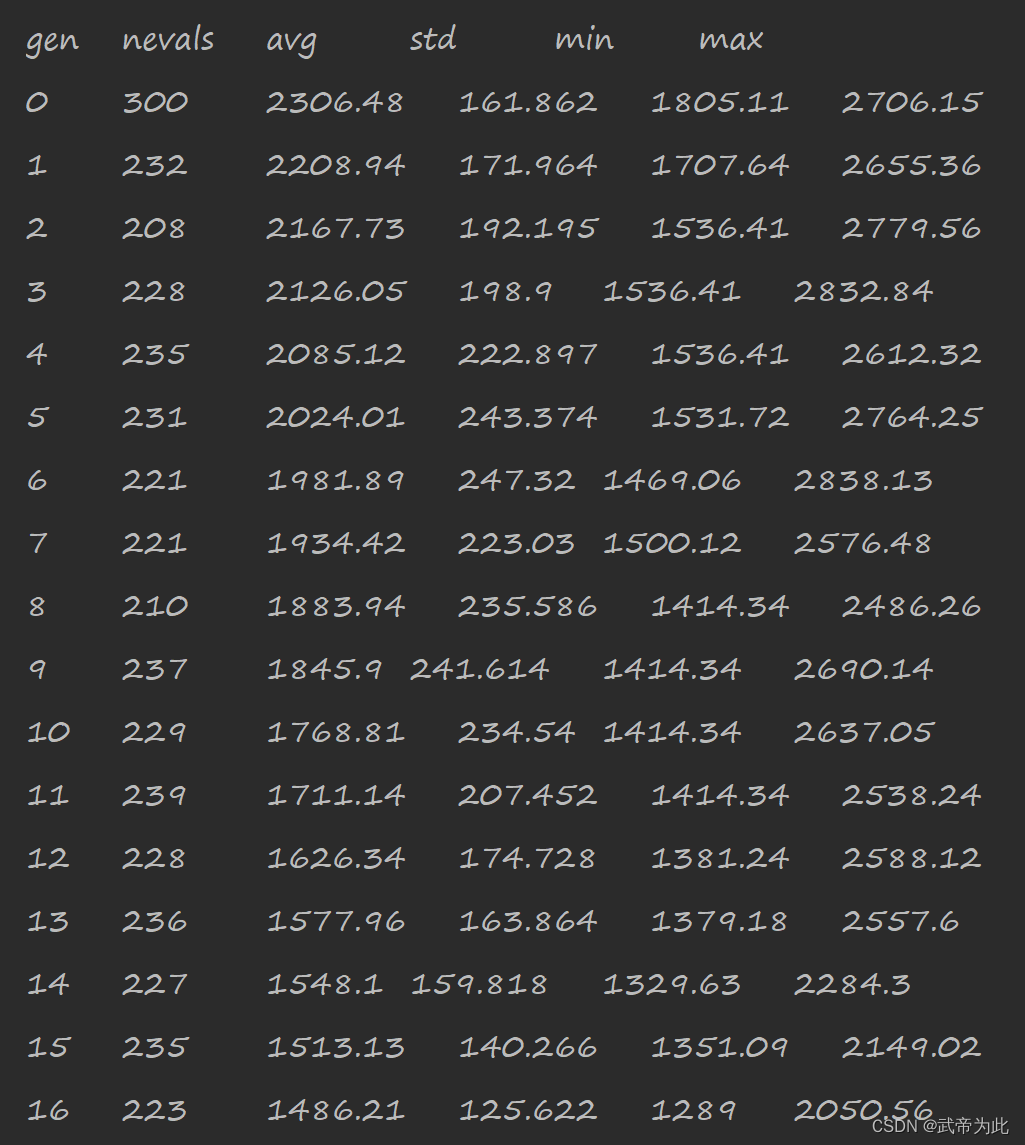
通过迭代，我们可以观察到解的适应度在逐步改善。

结果可视化

我们可以使用matplotlib库将最优路径可视化，以更好地理解遗传算法的结果。

def plot_path(individual):
    plt.figure()
    for i in range(len(individual)):
        city1 = CITIES[individual[i-1]]
        city2 = CITIES[individual[i]]
        plt.plot([city1[0], city2[0]], [city1[1], city2[1]], 'b-')
    plt.plot([CITIES[i][0] for i in individual], [CITIES[i][1] for i in individual], 'ro')
    plt.show()

pop, log, hof = main()
best_ind = hof[0]
plot_path(best_ind)