这是搬运的
一、 实验准备
1.1 实验概述
所谓聚类算法是指将一堆没有标签的数据自动划分成几类的方法,属于无监督学习方法,这个方法要保证同一类的数据有相似的特征。根据样本之间的距离或者说是相似性(亲疏性),把越相似、差异越小的样本聚成一类(簇),最后形成多个簇,使同一个簇内部的样本相似度高,不同簇之间差异性高。
K-means算法,也被称为K-平均或K-均值,是一种广泛使用的聚类算法,或者成为其他聚类算法的基础。简单的描述,就是我们输入n个数据,输出K个簇,并保证簇内数据具有极大的相似性、簇间数据存在明显的差异性。K-means算法主要用户来做图像识别、文本分类、用户分分群等。本章将会介绍K-means算法。
1.2 实验目的
- 学习了解K-means聚类算法基本概念
- 学习掌握K-means聚类算法原理、算法流程
- python实现K-means聚类算法的代码详解
- 使用Python的scipy实现k-means算法
- sklearn实现K-means聚类算法
- K-Means与KNN的相似与差别
- K-means聚类算法的优缺点总结
1.3 实验准备
服务器端:python3.6以上、Jupyter Notebook 客户端:Google Chrome浏览器
二、 实验步骤
2.1 K-means聚类算法概述
k-means算法又名k均值算法,是集简单和经典于一身的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为类簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。K-means算法中的k表示的是聚类为k个簇,means代表取每一个聚类中数据值的均值作为该簇的中心,或者称为质心,即用每一个的类的质心对该簇进行描述。
说白了就是无监督的聚类,大家都是同一个标注,或者没有标注,然后这一堆数据是一类,那一堆又是一类,你人为的设置好几个类,算法自动帮你分好各个类,只要每个类的样本尽可能的紧凑即可。
2.3 K-means算法原理
K-Means算法的思想很简单,对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
如果用数据表达式表示,假设簇划分为(𝐶1,𝐶2,...𝐶𝑘)(�1,�2,...��),则我们的目标是最小化平方误差E:
𝐸=∑𝑖=1𝑘∑𝑥∈𝐶𝑖||𝑥−𝜇𝑖||22�=∑�=1�∑�∈��||�−��||22
其中𝜇𝑖��是簇𝐶𝑖��的均值向量,有时也称为质心,表达式为:
𝜇𝑖=1|𝐶𝑖|∑𝑥∈𝐶𝑖𝑥��=1|��|∑�∈���
各类簇内的样本越相似,其与该类均值间的误差平方越小,对所有类所得到的误差平方求和,即可验证分为k类时,各聚类是否是最优的。
上式的代价函数无法用解析的方法最小化,只能有迭代的方法。
2.4 K-Meams算法流程
2.4.1 首先我们罗列K-Means算法的一些要点。
-
1、对于K-Means算法,首先要注意的是k值的选择,一般来说,我们会根据对数据的先验经验选择一个合适的k值,如果没有什么先验知识,则可以通过交叉验证选择一个合适的k值。
-
2、在确定了k的个数后,我们需要选择k个初始化的质心,就像上图b中的随机质心。由于我们是启发式方法,k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心,最好这些质心不能太近。
2.4.2 流程:
输入:样本集𝐷=𝑥1,𝑥2,...𝑥𝑚�=�1,�2,...��,聚类的簇树k,最大迭代次数N
输出:簇划分𝐶=𝐶1,𝐶2,...𝐶𝑘�=�1,�2,...��
-
1)从数据集D中随机选择k个样本作为初始的k个质心向量:μ1,μ2,...,μ𝑘μ1,μ2,...,μ�
-
2)对于𝑛=1,2,...,𝑁�=1,2,...,�
-
a) 将簇划分C初始化为𝐶𝑡=∅,𝑡=1,2...𝑘��=∅,�=1,2...�
-
b) 对于i=1,2...m,计算样本xi和各个质心向量μ𝑗(𝑗=1,2,...𝑘)μ�(�=1,2,...�)的距离:
𝑑𝑖𝑗=||𝑥𝑖−𝜇𝑗||22���=||��−��||22
将𝑥𝑖��标记最小的为𝑑𝑖𝑗���所对应的类别λ𝑖λ�。此时更新𝐶λ𝑖=𝐶λ𝑖∪𝑥𝑖�λ�=�λ�∪��
-
c) 对于𝑗=1,2,...,𝑘�=1,2,...,�,对𝐶𝑗��中所有的样本点重新计算新的质心:
𝜇𝑗=1|𝐶𝑗|∑𝑥∈𝐶𝑗𝑥��=1|��|∑�∈���
-
e) 如果所有的k个质心向量都没有发生变化,则转到步骤3)
-
-
3) 输出簇划分
2.5 python实现k-means(代码里面有注释,尝试去理解每一步的执行,对k-means有一个基本的了解。)
- 2.5.1、导入所需库,%matplotlib inline是为了使接下来的绘图能够显示在Jupyter notebook的浏览器上。
import numpy as np import matplotlib.pyplot as plt %matplotlib inline
In [1]:
#请在此编写代码
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
-
2.5.2、定义加载样本点数据的函数load_dataset
输入参数为文件名,将文件按行读取,每一行为一个列表,依次追加到空列表data_mat中,最后以矩阵的形式返回所得。
- @ param fileName:文件名
- @ return
# 解析文件,按tab分割字段,得到一个浮点数字类型的矩阵
def loadDataSet(fileName):
dataMat = [] # 初始化一个空列表,文件的最后一个字段是类别标签
fr = open(fileName) # 读取文件
for line in fr.readlines(): # 循环遍历文件所有行
curLine = line.strip().split('\t') # 切割每一行的数据
fltLine = list(map(float, curLine)) # 映射所有的元素为 float(浮点数)类型
dataMat.append(fltLine) # 将数据追加到dataMat
return dataMat # 返回dataMatIn [2]:
#请在此编写代码
def loadDataSet(fileName):
dataMat = [] # 初始化一个空列表,文件的最后一个字段是类别标签
fr = open(fileName) # 读取文件
for line in fr.readlines(): # 循环遍历文件所有行
curLine = line.strip().split('\t') # 切割每一行的数据
fltLine = list(map(float, curLine)) # 映射所有的元素为 float(浮点数)类型
dataMat.append(fltLine) # 将数据追加到dataMat
return dataMat # 返回dataMat
-
2.5.3、定义一个计算两个向量之间欧氏距离的函数dist_eclud 在此介绍欧氏距离是一个通常采用的距离定义,指在m维空间中两个点之间的真实距离,计算公式如下:
𝑑(𝑥,𝑦)=(𝑥1−𝑦1)2+(𝑥2−𝑦2)2+…+(𝑥𝑛−𝑦𝑛)2⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯√=∑𝑖=1𝑛(𝑥𝑖−𝑦𝑖)2⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯�(�,�)=(�1−�1)2+(�2−�2)2+…+(��−��)2=∑�=1�(��−��)2
# 计算欧几里得距离
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) # 求两个向量之间的距离In [3]:
#请在此编写代码
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) # 求两个向量之间的距离
-
2.5.4、为给定数据集构建一个包含K个随机质心的集合。
随机质心必须要在整个数据集的边界之内。首先可以找到数据集每一维的最小和最大值。然后得到每一维的取值范围。用0到1之间的随机数和取值范围相乘,再用最小值加上该乘积,就可以得到在每一维取值范围内的随机数。
- @ param dataMat:数据集
- @ param k:质心个数
- @ return:返回质心
# 构建聚簇中心,取k个(此例中为4)随机质心
def randCent(dataSet, k):
n = shape(dataSet)[1] # 获取特征值
centroids = mat(zeros((k,n))) #初始化质心,创建(k,n)个以零填充的矩阵
for j in range(n): #循环遍历特征值
minJ = min(dataSet[:,j]) #计算每一列的最小值
maxJ = max(dataSet[:,j]) #计算每一列的最大值
rangeJ = float(maxJ - minJ) #计算每一列的范围值
centroids[:,j] = minJ + rangeJ * random.rand(k, 1) # 计算每一列的质心,并将值赋给centroids
return centroids #返回质心In [4]:
#请在此编写代码
def randCent(dataSet, k):
n = shape(dataSet)[1] # 获取特征值
centroids = mat(zeros((k,n))) #初始化质心,创建(k,n)个以零填充的矩阵
for j in range(n): #循环遍历特征值
minJ = min(dataSet[:,j]) #计算每一列的最小值
maxJ = max(dataSet[:,j]) #计算每一列的最大值
rangeJ = float(maxJ - minJ) #计算每一列的范围值
centroids[:,j] = minJ + rangeJ * random.rand(k, 1) # 计算每一列的质心,并将值赋给centroids
return centroids #返回质心
-
2.5.5、k-means聚类算法
计算误差的多少,通过这个方法来确定 k 为多少比较合适,kMeans方法将执行一个简化的 kMeans ,即较少次数的迭代,计算出其中的误差(即当前点到簇质心的距离,后面会使用该误差来评价聚类的效果)
- @ param dataSet :数据集
- @ param k : 簇的数目
- @ param distMeans : 计算距离
- @ param createCent :创建初始质心
- @ return : 返回所有的类质心与点分配结果
def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent):
m = shape(dataSet)[0]
# clusterAssment包含两个列:一列记录簇索引值,第二列存储误差(误差是指当前点到簇质心的距离,后面会使用该误差来评价聚类的效果)
clusterAssment = mat(zeros((m,2)))
centroids = createCent(dataSet, k) # 创建质心,随机K个质心
clusterChanged = True # 用来判断聚类是否已经收敛
while clusterChanged:
clusterChanged = False;
# 遍历所有数据找到距离每个点最近的质心,
# 可以通过对每个点遍历所有质心并计算点到每个质心的距离来完成
for i in range(m):
minDist = inf; minIndex = -1;
for j in range(k):
# 计算数据点到质心的距离
# 计算距离是使用distMeans参数给出的距离公式,默认距离函数是distEclud
distJI = distMeans(centroids[j,:], dataSet[i,:])
#如果距离比minDist(最小距离)还小,更新minDist(最小距离)和最小质心的index(索引)
if distJI < minDist:
minDist = distJI; minIndex = j # 如果第i个数据点到第j个中心点更近,则将i归属为j
# 如果任一点的簇分配结果发生改变,则更新clusterChanged标志
if clusterAssment[i,0] != minIndex: clusterChanged = True;
clusterAssment[i,:] = minIndex,minDist**2 # 更新簇分配结果为最小质心的index(索引),minDist(最小距离)的平方
print(centroids)
for cent in range(k): # 重新计算中心点,遍历所有质心并更新它们的取值
ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]] # 通过数据过滤来获得给定簇的所有点
centroids[cent,:] = mean(ptsInClust, axis = 0) # 计算所有点的均值,axis=0表示沿矩阵的列方向进行均值计算
return centroids, clusterAssment #返回所有的类质心与点分配结果In [5]:
#请在此编写代码
def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent):
m = shape(dataSet)[0]
# clusterAssment包含两个列:一列记录簇索引值,第二列存储误差(误差是指当前点到簇质心的距离,后面会使用该误差来评价聚类的效果)
clusterAssment = mat(zeros((m,2)))
centroids = createCent(dataSet, k) # 创建质心,随机K个质心
clusterChanged = True # 用来判断聚类是否已经收敛
while clusterChanged:
clusterChanged = False;
# 遍历所有数据找到距离每个点最近的质心,
# 可以通过对每个点遍历所有质心并计算点到每个质心的距离来完成
for i in range(m):
minDist = inf; minIndex = -1;
for j in range(k):
# 计算数据点到质心的距离
# 计算距离是使用distMeans参数给出的距离公式,默认距离函数是distEclud
distJI = distMeans(centroids[j,:], dataSet[i,:])
#如果距离比minDist(最小距离)还小,更新minDist(最小距离)和最小质心的index(索引)
if distJI < minDist:
minDist = distJI; minIndex = j # 如果第i个数据点到第j个中心点更近,则将i归属为j
# 如果任一点的簇分配结果发生改变,则更新clusterChanged标志
if clusterAssment[i,0] != minIndex: clusterChanged = True;
clusterAssment[i,:] = minIndex,minDist**2 # 更新簇分配结果为最小质心的index(索引),minDist(最小距离)的平方
print(centroids)
for cent in range(k): # 重新计算中心点,遍历所有质心并更新它们的取值
ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]] # 通过数据过滤来获得给定簇的所有点
centroids[cent,:] = mean(ptsInClust, axis = 0) # 计算所有点的均值,axis=0表示沿矩阵的列方向进行均值计算
return centroids, clusterAssment #返回所有的类质心与点分配结果
- 2.5.6、为了清晰直观,用绘图库绘制散点图。
def showCluster(dataSet,k,centroids,clusterAssment):
m,n = dataSet.shape
if n != 2:
print("数据不是二维的")
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
if k > len(mark):
print("k值太大了")
return 1
# 绘制所有的样本
for i in range(m):
markIndex = int(clusterAssment[i,0])
plt.plot(dataSet[i,0],dataSet[i,1],mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']
# 绘制质心
for i in range(k):
plt.plot(centroids[i,0],centroids[i,1],mark[i],markersize=13)
plt.show()In [6]:
#请在此编写代码
def showCluster(dataSet,k,centroids,clusterAssment):
m,n = dataSet.shape
if n != 2:
print("数据不是二维的")
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
if k > len(mark):
print("k值太大了")
return 1
# 绘制所有的样本
for i in range(m):
markIndex = int(clusterAssment[i,0])
plt.plot(dataSet[i,0],dataSet[i,1],mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']
# 绘制质心
for i in range(k):
plt.plot(centroids[i,0],centroids[i,1],mark[i],markersize=13)
plt.show()
-
2.5.7、用测试数据及测试kmeans算法
采用二维数据集,共 80 个样本,有 4 个类。
from numpy import *
datMat = np.mat(loadDataSet('./dataset/data.txt'))
k = 4
centroids,clusterAssment = kMeans(datMat,4)
print(centroids)
print(clusterAssment)
In [7]:
#请在此处编写代码
from numpy import *
datMat = np.mat(loadDataSet('./dataset/data.txt'))
k = 4
centroids,clusterAssment = kMeans(datMat,4)
print(centroids)
print(clusterAssment)
[[ 2.16077677 4.85721025 0.46208468] [ 0.5598126 0.0642959 0.93248342] [-1.50504287 -1.76940597 0.04974545] [-1.55648717 7.08504587 0.680824 ]] [[ 1.06826229e+00 4.90619006e+00 1.00000000e+00] [-5.03866667e-02 1.41018433e+00 1.00000000e+00] [-1.42628420e+00 -1.46919310e+00 1.00000000e+00] [-2.42408621e-03 9.78870578e+00 1.89655172e-01]] [[ 0.35940771 5.23815296 0.91666667] [-0.028896 1.74008831 1. ] [-1.28849545 -1.40065736 1. ] [ 0.18390247 10.6012479 0.08163265]] [[ 0.17240308 5.71646988 0.84615385] [ 0.1499875 1.90216956 1. ] [-1.28849545 -1.40065736 1. ] [ 0.22205367 10.8922436 0.04444444]] [[ 0.16020719 5.97991278 0.81481481] [ 0.24184622 2.07192589 1. ] [-1.29257683 -1.24490767 1. ] [ 0.22868177 11.0185484 0.02325581]] [[ 0.32956554 6.23157885 0.80769231] [ 0.16009026 2.37227847 1. ] [-1.187105 -1.14455046 1. ] [ 0.16245633 11.08085274 0. ]] [[ 0.37641704 6.31607868 0.8 ] [ 0.12615484 2.56569521 1. ] [-1.11637957 -1.03107079 1. ] [ 0.16245633 11.08085274 0. ]] [[ 0.42758579 6.39692817 0.79166667] [ 0.07726545 2.656195 1. ] [-1.11637957 -1.03107079 1. ] [ 0.16245633 11.08085274 0. ]] [[ 5.06856217e-01 6.47233630e+00 7.82608696e-01] [ 7.12738095e-03 2.75173529e+00 1.00000000e+00] [-1.11637957e+00 -1.03107079e+00 1.00000000e+00] [ 1.62456333e-01 1.10808527e+01 0.00000000e+00]] [[ 5.06856217e-01 6.47233630e+00 7.82608696e-01] [ 7.12738095e-03 2.75173529e+00 1.00000000e+00] [-1.11637957e+00 -1.03107079e+00 1.00000000e+00] [ 1.62456333e-01 1.10808527e+01 0.00000000e+00]] [[3.00000000e+00 8.86646439e+00] [1.00000000e+00 5.61891797e+00] [0.00000000e+00 2.20198418e+00] [0.00000000e+00 4.42165156e+00] [3.00000000e+00 6.87574580e-02] [0.00000000e+00 4.11312894e-01] [3.00000000e+00 3.01255196e+00] [0.00000000e+00 9.00599043e+00] [3.00000000e+00 2.51293558e+00] [3.00000000e+00 4.62306728e-01] [0.00000000e+00 3.66005920e-01] [3.00000000e+00 5.79112443e+00] [1.00000000e+00 1.54062584e+00] [3.00000000e+00 7.71230015e+00] [0.00000000e+00 1.72279118e+00] [1.00000000e+00 2.20549357e+00] [0.00000000e+00 4.32013774e-01] [1.00000000e+00 5.58948233e-03] [2.00000000e+00 3.02167320e+00] [0.00000000e+00 8.20353537e-01] [1.00000000e+00 4.14248861e+00] [2.00000000e+00 5.57245147e-01] [3.00000000e+00 1.03339411e+00] [2.00000000e+00 1.01169824e+00] [1.00000000e+00 4.55004991e+00] [3.00000000e+00 3.31576954e+00] [3.00000000e+00 4.73248589e+00] [2.00000000e+00 6.72335164e+00] [1.00000000e+00 6.91713227e-01] [3.00000000e+00 3.70924663e+00] [1.00000000e+00 1.68633497e+00] [0.00000000e+00 3.37181008e+00] [3.00000000e+00 1.38525753e+00] [2.00000000e+00 1.94412739e+00] [0.00000000e+00 2.83488654e+00] [3.00000000e+00 2.37571735e+00] [3.00000000e+00 3.15171637e+00] [3.00000000e+00 6.57683051e+00] [3.00000000e+00 4.00159514e+00] [3.00000000e+00 1.86850065e+00] [1.00000000e+00 5.02676844e-01] [0.00000000e+00 4.68697611e-01] [3.00000000e+00 1.18773861e+00] [1.00000000e+00 6.16531451e+00] [1.00000000e+00 6.80437853e-01] [3.00000000e+00 2.24334840e+00] [2.00000000e+00 1.47567652e+00] [0.00000000e+00 4.27148153e-01] [3.00000000e+00 1.48478443e+00] [3.00000000e+00 1.16861567e-01] [3.00000000e+00 5.56710982e+00] [3.00000000e+00 8.38340420e-01] [0.00000000e+00 3.94650758e+00] [3.00000000e+00 7.45854945e+00] [0.00000000e+00 3.13459718e+00] [0.00000000e+00 3.45192990e-01] [3.00000000e+00 3.88542234e-01] [0.00000000e+00 3.23656897e+00] [3.00000000e+00 1.39890752e+00] [0.00000000e+00 3.78141546e+00] [1.00000000e+00 2.59018504e+00] [1.00000000e+00 8.59569118e-01] [3.00000000e+00 4.04904980e+00] [3.00000000e+00 1.90621764e+00] [3.00000000e+00 1.47318614e+00] [2.00000000e+00 2.82543898e-01] [0.00000000e+00 4.14353425e+00] [3.00000000e+00 1.56388962e+00] [3.00000000e+00 1.01801881e+00] [3.00000000e+00 8.99470693e-01] [3.00000000e+00 1.09561366e-02] [2.00000000e+00 2.29711157e+00] [3.00000000e+00 7.26775736e+00] [1.00000000e+00 3.90114771e-02] [3.00000000e+00 1.55188885e+00] [0.00000000e+00 2.08009287e+00] [2.00000000e+00 1.30109199e+00] [1.00000000e+00 2.06047618e+00] [0.00000000e+00 4.55711065e+00] [1.00000000e+00 3.37470155e+00] [0.00000000e+00 4.84875741e+00] [2.00000000e+00 4.62759416e+00] [3.00000000e+00 3.38607577e+00] [0.00000000e+00 1.00364377e+01] [1.00000000e+00 2.35548111e+00] [2.00000000e+00 5.73171843e-01] [1.00000000e+00 1.93306807e+00] [3.00000000e+00 3.92784870e+00] [0.00000000e+00 2.60809755e+00] [2.00000000e+00 2.61773285e+00] [2.00000000e+00 1.55359627e+00] [3.00000000e+00 5.36787777e+00] [3.00000000e+00 1.78669403e+00] [1.00000000e+00 3.36095175e+00] [1.00000000e+00 2.81645473e+00] [1.00000000e+00 4.88099288e-01] [3.00000000e+00 5.08434258e-01] [2.00000000e+00 2.48749645e+00] [3.00000000e+00 4.52707209e+00] [3.00000000e+00 1.34061170e+01]]
print('show the result!')
showCluster(datMat[:,0:2],k,centroids,clusterAssment)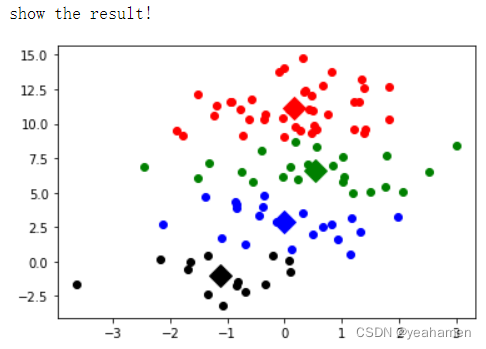
In [8]:
#请在此编写代码
print('show the result!')
showCluster(datMat[:,0:2],k,centroids,clusterAssment)
show the result!

2.6 使用Python的scipy实现k-means
假设要解决这个问题。
以下是一些同学,大萌是一个学霸,而我们想要找到这些人中的潜在学霸,所以我们要把这些人分为两类——学霸与非学霸。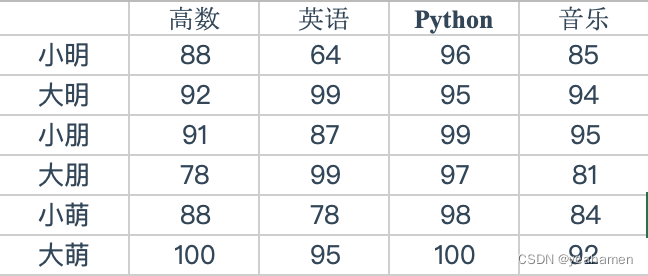
- 2.6.1、导入所需包
import numpy as np from scipy.cluster.vq import vq,kmeans,whiten
In [9]:
#请在此编写代码
import numpy as np
from scipy.cluster.vq import vq,kmeans,whiten
- 2.6.2、创建数据集
list1=[88.0,74.0,96.0,85.0] list2=[92.0,99.0,95.0,94.0] list3=[91.0,87.0,99.0,95.0] list4=[78.0,99.0,97.0,81.0] list5=[88.0,78.0,98.0,84.0] list6=[100.0,95.0,100.0,92.0] data=np.array([list1, list2, list3, list4, list5, list6])
In [10]:
#请在此编写代码
list1=[88.0,74.0,96.0,85.0]
list2=[92.0,99.0,95.0,94.0]
list3=[91.0,87.0,99.0,95.0]
list4=[78.0,99.0,97.0,81.0]
list5=[88.0,78.0,98.0,84.0]
list6=[100.0,95.0,100.0,92.0]
data=np.array([list1, list2, list3, list4, list5, list6])
- 2.6.3、实现
- whiten()算出各列元素的标准差,形成一个新的数组
- kmeans()函数的功能是对数据进行聚类,返回结果是一个元组,其中我们只需要它的第一个值,这是一个聚类中心数组。
- vq()函数的功能是矢量量化数据,它可以对每一个数据,也就是对我们这边的每一个人进行归类。
whiten_=whiten(data) centroids,_=kmeans(whiten_,2) result,_=vq(whiten_,centroids) print(result)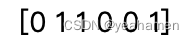
说明大明、小朋和大萌都是学霸组的。
需要说明的是,kmeans找到的只是一个局部最优解,而不是全局。
In [11]:
#请在此编写代码
whiten_=whiten(data)
centroids,_=kmeans(whiten_,2)
result,_=vq(whiten_,centroids)
print(result)
[1 0 0 1 1 0]
2.7 sklearn实现k-means
格式如下:
sklearn.cluster.KMeans(n_clusters=8,init='k-means++',
n_init=10, max_iter=300,
tol=0.0001, precompute_distances='auto',
verbose=0, random_state=None,
copy_x=True, n_jobs=1, algorithm='auto')参数详解:
- n_clusters:簇的个数,即你想聚成几类
- init: 初始簇中心的获取方法
- n_init: 获取初始簇中心的更迭次数,为了弥补初始质心的影响,算法默认会初始10个质心,实现算法,然后返回最好的结果。
- max_iter: 最大迭代次数(因为kmeans算法的实现需要迭代)
- tol: 容忍度,即kmeans运行准则收敛的条件
- precompute_distances:是否需要提前计算距离,这个参数会在空间和时间之间做权衡,如果是True 会把整个距离矩阵都放到内存中,auto 会默认在数据样本大于featurs*samples 的数量大于12e6 的时候False,False 时核心实现的方法是利用Cpython 来实现的
- verbose: 冗长模式(不太懂是啥意思,反正一般不去改默认值)
- random_state: 随机生成簇中心的状态条件。
- copy_x: 对是否修改数据的一个标记,如果True,即复制了就不会修改数据。bool 在scikit-learn 很多接口中都会有这个参数的,就是是否对输入数据继续copy 操作,以便不修改用户的输入数据。这个要理解Python 的内存机制才会比较清楚。
- n_jobs: 并行设置
- algorithm: kmeans的实现算法,有:’auto’, ‘full’, ‘elkan’, 其中 ‘full’表示用EM方式实现
注意:虽然有很多参数,但是都已经给出了默认值。所以我们一般不需要去传入这些参数,参数的。可以根据实际需要来调用。
2.7.1 案例
- 2.7.1.1、导入所需包
from sklearn.datasets import make_blobs import matplotlib.pyplot as plt
In [12]:
#请在此编写代码
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
- 2.7.2.2、模拟数据,make_blobs创建数据集,并画出图像
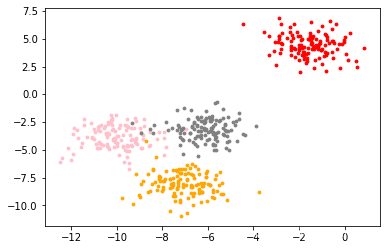
X, y = make_blobs(n_samples=500, # 500个样本
n_features=2, # 每个样本2个特征
centers=4, # 4个中心
random_state=1 #控制随机性
)
color = ['red', 'pink','orange','gray']
fig, axi1=plt.subplots(1)
for i in range(4):
axi1.scatter(X[y==i, 0], X[y==i,1],
marker='o',
s=8,
c=color[i]
)
plt.show()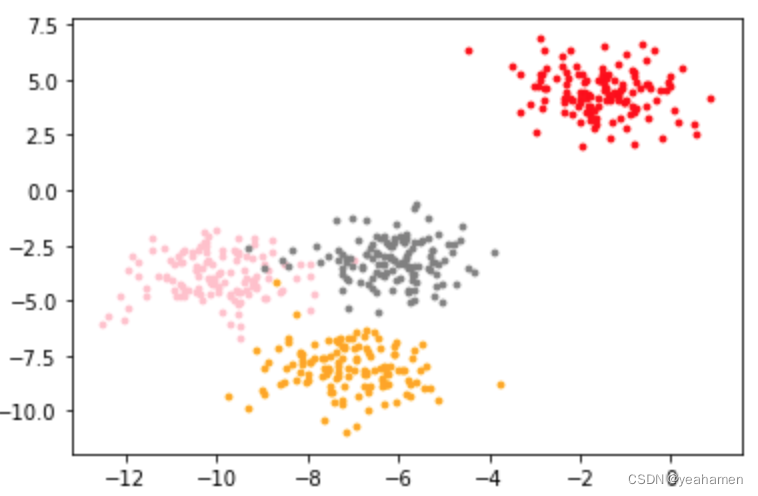
In [13]:
#请在此编写代码
X, y = make_blobs(n_samples=500, # 500个样本
n_features=2, # 每个样本2个特征
centers=4, # 4个中心
random_state=1 #控制随机性
)
color = ['red', 'pink','orange','gray']
fig, axi1=plt.subplots(1)
for i in range(4):
axi1.scatter(X[y==i, 0], X[y==i,1],
marker='o',
s=8,
c=color[i]
)
plt.show()
- 2.7.2.3、调用 sklearn.cluster 模块中的KMeans函数建模并评估
from sklearn.cluster import KMeans
n_clusters=3
cluster = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
print("kmean: k={}, cost={}".format(n_clusters, int(cluster.score(X))))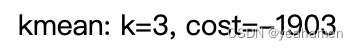
In [14]:
#请在此编写代码
from sklearn.cluster import KMeans
n_clusters=3
cluster = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
print("kmean: k={}, cost={}".format(n_clusters, int(cluster.score(X))))
kmean: k=3, cost=-1903
- 2.7.2.4、查看其属性:质心、inertia
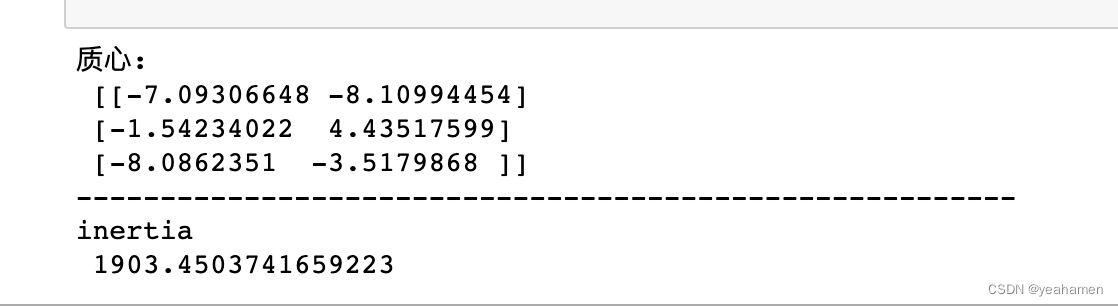
centroid=cluster.cluster_centers_
print("质心:\n",centroid)
print("-"*56)
inertia=cluster.inertia_
print("inertia\n",inertia)
In [15]:
#请在此编写代码
centroid=cluster.cluster_centers_
print("质心:\n",centroid)
print("-"*56)
inertia=cluster.inertia_
print("inertia\n",inertia)
质心: [[-7.09306648 -8.10994454] [-1.54234022 4.43517599] [-8.0862351 -3.5179868 ]] -------------------------------------------------------- inertia 1903.4503741659223
- 2.7.2.5、画出所在位置。
y_pred=cluster.labels_ # 获取聚类标签
color=['red','pink','orange','gray'] # 绘制k-means结果
fig, axi1=plt.subplots(1)
for i in range(n_clusters):
axi1.scatter(X[y_pred==i, 0], X[y_pred==i, 1],
marker='o',
s=8,
c=color[i])
axi1.scatter(centroid[:,0],centroid[:,1],marker='x',s=100,c='black')
plt.show()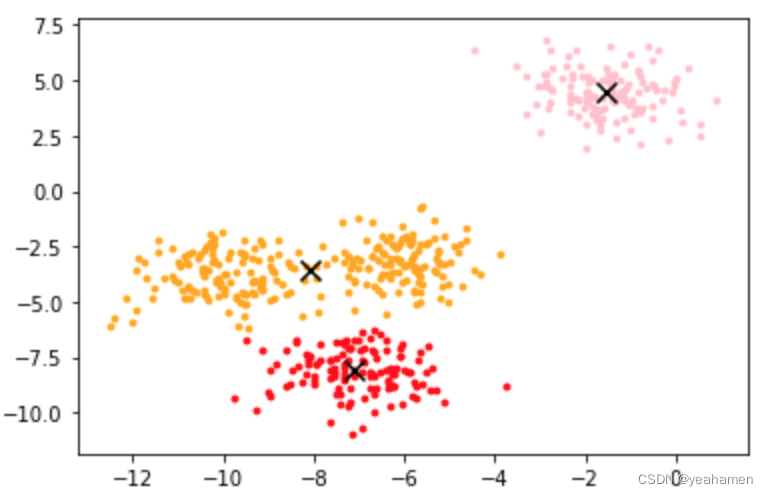
In [17]:
#请在此编写代码
y_pred=cluster.labels_ # 获取聚类标签
color=['red','pink','orange','gray'] # 绘制k-means结果
fig, axi1=plt.subplots(1)
for i in range(n_clusters):
axi1.scatter(X[y_pred==i, 0], X[y_pred==i, 1],
marker='o',
s=8,
c=color[i])
axi1.scatter(centroid[:,0],centroid[:,1],marker='x',s=100,c='black')
plt.show()

2.8 K-Means与KNN
初学者很容易把K-Means和KNN搞混,两者其实差别还是很大的。
- K-Means是无监督学习的聚类算法,没有样本输出;而KNN是监督学习的分类算法,有对应的类别输出。
- KNN基本不需要训练,对测试集里面的点,只需要找到在训练集中最近的k个点,用这最近的k个点的类别来决定测试点的类别。而K-Means则有明显的训练过程,找到k个类别的最佳质心,从而决定样本的簇类别。
- 当然,两者也有一些相似点,两个算法都包含一个过程,即找出和某一个点最近的点。
- 两者都利用了最近邻(nearest neighbors)的思想。
2.9 K-Means优缺点总结
-
优点
- 1)原理比较简单,实现也是很容易,收敛速度快。
- 2)聚类效果较优。
- 3)算法的可解释度比较强。
- 4)主要需要调参的参数仅仅是簇数k。
-
缺点
- 1)K值的选取不好把握
- 2)对于不是凸的数据集比较难收敛
- 3)如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳。
- 4) 采用迭代方法,得到的结果只是局部最优。
- 5) 对噪音和异常点比较的敏感。
三、 实验小结
<此处可填写你实验过程中遇到的问题、解决过程以及实验结果>