1.概述

（1）单调栈是一种特殊的栈，它在普通栈的基础上要求从栈顶到栈底的元素是单调的，如果栈中的元素从栈顶到栈底是单调递增的，那么我们将该栈称为单调递增栈 。如果栈中的元素从栈顶到栈底是单调递减的，则称为单调递增栈。

（2）单调栈的主要作用在于在时间复杂度为 O(n) 的情况下，找到数组中所有元素的左边或者右边第一个比它小或者大的元素，主要思想在于用空间来换时间，即用单调栈来存储相关信息，这样一来虽然空间复杂度增加了，但是时间复杂度缺降低了。

（3）我们以 nums = [2, 0, 6, 4, 7, 3, -1, 9] 为例，来说明一下单调递增栈的进栈、出栈过程，从左往右开始遍历数组 nums：

第 i 步	待插入元素	操作	栈中元素（栈顶 → 栈底）	结果
1	2	2 入栈	[2]	元素 2 的左侧没有比 2 大的元素
2	0	0 入栈	[0, 2]	元素 0 的左侧第一个比 0 大的元素为 2
3	6	0、2 出栈，6 入栈	[6]	元素 6 的左侧没有比 6 大的元素
4	4	4 入栈	[4, 6]	元素 4 的左侧第一个比 4 大的元素为 6
5	7	4、6 出栈，7 入栈	[7]	元素 7 的左侧没有比 7 大的元素
6	3	3 入栈	[3, 7]	元素 3 的左侧第一个比 3 大的元素为 7
7	-1	-1 入栈	[-1, 3, 7]	元素 -1 的左侧第一个比 -1 大的元素为 3
7	9	-1、3、7 出栈，9 入栈	[9]	元素 9 的左侧没有比 9 大的元素

2.代码框架

2.1.单调递增栈

class Solution {
    public void increasingStack(int[] nums) {
        //单调递增栈
        Deque<Integer> incrStack = new ArrayDeque<>();
        for (int i = 0; i < nums.length; i++) {
            //当前元素比栈顶元素小时才能入栈，否则需要先将栈顶元素进行出栈操作
            while (!incrStack .isEmpty() && incrStack .peek() <= nums[i]) {
                incrStack .pop();
                //其它操作
            }
            incrStack .push(nums[i]);
        }
    }
}

2.2.单调递减栈

class Solution {
    public void increasingStack(int[] nums) {
        //单调递减栈
        Deque<Integer> descStack = new ArrayDeque<>();
        for (int i = 0; i < nums.length; i++) {
            //当前元素比栈顶元素大时才能入栈，否则需要先将栈顶元素进行出栈操作
            while (!descStack.isEmpty() && descStack.peek() >= nums[i]) {
                descStack.pop();
                //其它操作
            }
            descStack.push(nums[i]);
        }
    }
}

上述代码理解起来并不算困难，但是有一些细节需要注意：

上面代码中的栈存储的是数组 nums 中元素，但是在有些场景下，则需要存储元素所对应的下标（通过下标可以找到对应的元素，因此存储下标时可使用的信息更多），例如在使用单调栈解决 LeetCode 中的 739.每日温度这题时，存储就是元素的下标，在这种情况下，主要原因在于要求解的问题与元素之间的距离有关。
上面的代码只是给出了单调栈最基础的框架，具体如何使用需要根据具体的情况而定。
具体使用单调栈的类别可以总结为一句话：查找比当前元素大的元素就用单调递增栈，查找比当前元素小的元素使用单调递减栈。
一般来说，遍历线性表的顺序是从左往右，但在有些情况下，从右往左遍历会更加合适，例如 LeetCode 中的 496.下一个更大元素 I这题。
总的来说，单调栈的代码框架如下所示，其中出栈的条件便决定了使用的单调栈类型：

class Solution {
    public void monotonousStack() {
        Deque<Integer> stack = new ArrayDeque<>();
        for (遍历数组/字符串等线性表) {
            while (!stack.isEmpty() && 出栈的条件) {
                stack.pop();
                //其它操作
            }
            stack.push(元素/元素下标);
        }
    }
}

3.应用

3.1.应用一

下面我们以 LeetCode 中的 739. 每日温度这题为例，来说明单调栈的作用：

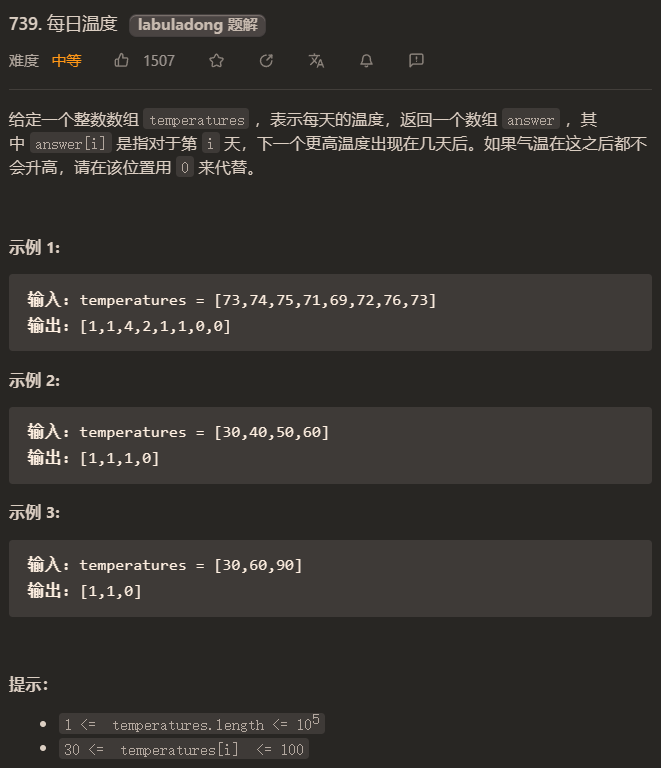
在这里插入图片描述

题目要求比较简单，一般来说，暴力穷举法是一种比较容易想到的方法，即使用 2 层 for 循环来求出每一天后面第一次温度高于当天的日期，然后将天数之差的结果存储到数组 answer 中即可。具体代码如下：

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        int[] answer = new int[n];
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (temperatures[j] > temperatures[i]) {
                    answer[i] = j - i;
                    break;
                }
            }
        }
        return answer;
    }
}

但是上述代码的时间复杂度为 O(n²)，那么我们可不可以再优化一下呢？答案是肯定的。通过仔细分析题目可知，题目就是要求解数组 temperatures 中每个元素与其右边第一个比它大的元素之间的距离，这时我们可以使用单调栈来解决本题：

首先，我们需要查找数组中比当前元素大的元素，因此使用单调递增栈，具体体现在 while 循环的第二个判断条件；
其次，由于本题涉及到元素之间的距离问题（即下一个更高温度出现在几天后），因此单调栈中存储元素下标更为合适；
最后，将上面的代码框架应用到本题即可。

class Solution {
	public int[] dailyTemperatures(int[] temperatures) {
	    int length = temperatures.length;
	    int[] answer = new int[length];
	    Deque<Integer> descStack = new ArrayDeque<>();
	    for (int i = 0; i < length; i++) {
	    	/*
	    		temperatures[descStack.peek()] < temperatures[i]: 说明第 i 天的温度高于第 j 天 (j < i，
	    		且 j = descStack.peek()) 的温度，那么此时第 j 天下一个更高温度出现在 i - j 天之后
			*/
	        while (!descStack.isEmpty() && temperatures[descStack.peek()] < temperatures[i]) {
	            answer[descStack.peek()] = i - descStack.peek();
                descStack.pop();
	        }
	        descStack.push(i);
	    }
	    return answer;
	}
}

3.2.应用二

在应用一中，我们可以较为明显地判断出要使用单调栈，但是有些题目可能不太明显，例如 LeetCode 中的 84.柱状图中最大的矩形这题：

在这里插入图片描述

具体细节可以参考本题官方题解，使用单调栈的代码如下所示：

class Solution {
    public int largestRectangleArea(int[] heights) {
        int length = heights.length;
        int maxArea = 0;
        //定义单调栈，此处存储数组元素的下标，保证下标对应的值从栈底到栈顶逐渐递增
        Deque<Integer> stack = new ArrayDeque<>();
        for (int i = 0; i <= length; i++) {
            while (!stack.isEmpty() && (i == length || heights[stack.peek()] >= heights[i])) {
                int j = stack.pop();
                int left = stack.isEmpty() ? 0 : stack.peek() + 1;
                //计算以 heights[j] 为高的矩形面积
                int curArea = (i - left) * heights[j];
                maxArea = Math.max(maxArea, curArea);
            }
            //将当前下标加入到栈中
            stack.push(i);
        }
        return maxArea;
    }
}