1. 位图应用

题目一

给40亿个不重复的无符号整数，没排过序，给一个无符号整数，如何快速判断一个数是否在这40亿个数中

---

正常思路：
1.排序 + 二分查找
2.放入 哈希表 或者 红黑树

---

10亿字节 约等于 1GB
40亿个整数约等于 16GB
如果使用上述的两种方法，内存不够

---

哈希 的 直接定址法 的 哈希映射 ，判断整形在不在
依次映射标记，将值存起来
最少用一个char来表示一个值在不在 ，这样即为40亿字节即4GB，但是这样还是太大
标识在不在，并不需要将值存起来，使用0/1去表示

---

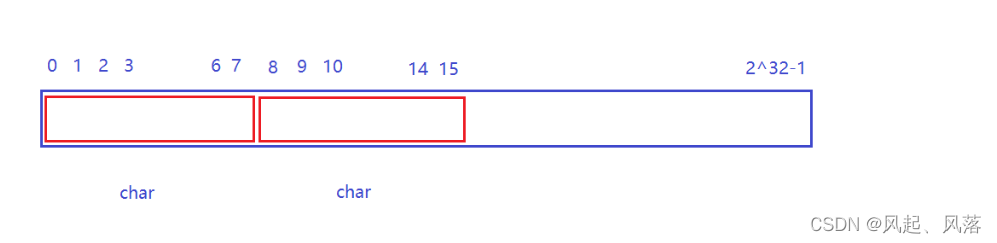
将每一个整数 所代表的值 用一个比特位去标识 即 位图
需要40亿个比特位，10亿字节 约等于 1GB ，40亿个比特位 约等于 500MB

代码实现

在bitset类中，
通过控制char，从而控制比特位

---

set

set 将x映射的比特位设置成1

由于下标从0开始计算
所以将0-7比特位算位第0个char ，8-15算为第1个char中，依次存储到对应的char
先计算在第几个char中，在计算在对应char的第几个比特位上面

---

---

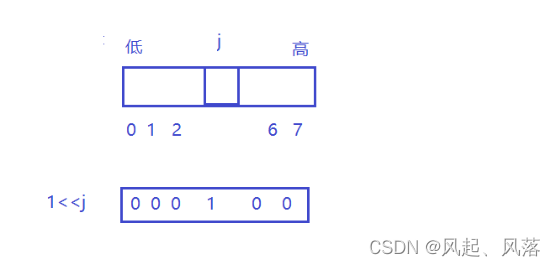
j 代表要寻找对应比特位的位置 ，想要将其置为1
<<是低到高的移位
1<<j 即 除了j位置 其他位置 都为0

所以 | 1 ，无论该位置的数为1/0 ，|后都为1

rset

rset将x映射的比特位设置成0

---

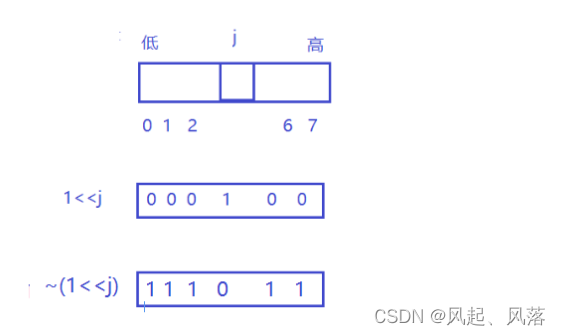
j 代表要寻找对应比特位的位置 ，想要将其置为 0
所以 &0 ，无论该位置的数为1/0 ，&后都为0

test

test 判断在不在

---

---

---

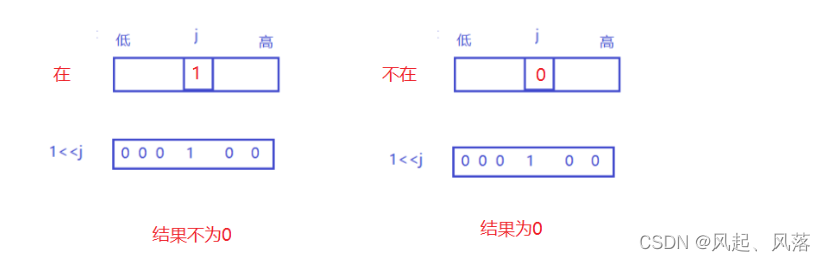
j 代表要寻找对应比特位的位置 将当前位置值 &1
由于在其他位置上也有可能存在11，所以结果不为0，则说明该位置存在
若结果为0， 则说明该位置不存在

具体代码

template<size_t N>
class bitset
{
public:
	bitset()
	{
		_bits.resize((N / 8) + 1, 0);
	}
	void set(size_t x)
	{
		size_t i = x / 8;//第几个char上
		size_t j = x % 8;//char上的第几个比特位
		_bits[i] |= (1 << j);
	}
	void rset(size_t x)
	{
		size_t i = x / 8;//第几个char上
		size_t j = x % 8;//char上的第几个比特位
		_bits[i] &= ~(1 << j);
	}
	bool test(size_t x)//判断在不在
	{
		size_t i = x / 8;//第几个char上
		size_t j = x % 8;//char上的第几个比特位
		return _bits[i] & (1 << j);
	}
private:
	vector<char> _bits;
};

题目二

给定100亿个整数，设计算法找到只出现一次的整数？

---

用 2个比特位表示 当前数据
00 表示 0次 01 表示 1次 10 表示 1次以上

---

将题目一的代码进行封装即可

---

---

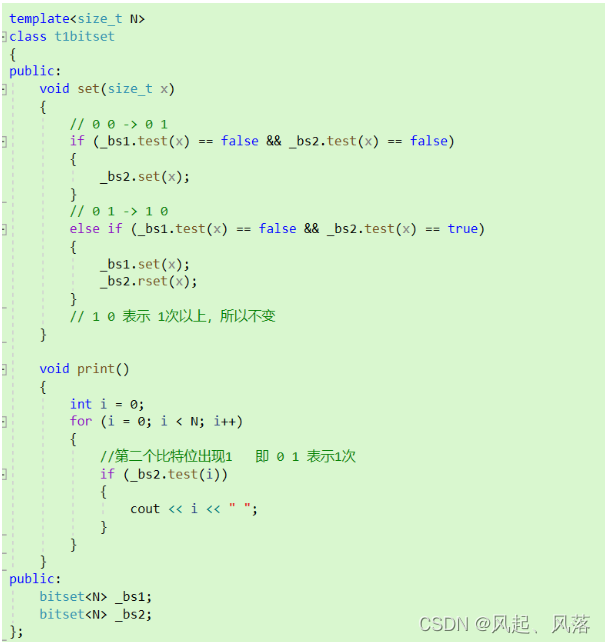
题目一的类为bitset，所以借此 来定义出 两个比特位 _bs1 _bs2
通过判断 两个比特位 是 1 /0
若出现次数为0，则 +1 变为 0 1
若出现次数为1 ， 则+1 变为 1 0
若出现次数为1次以上，则不变
最终通过类中的print函数打印出出现一次的数

位图优缺点总结

优点：

速度快 节省空间

缺点：
只能映射整形，string 浮点数 不能存储映射

---

所以提出布隆过滤器，用于一定程度解决 不能存储string类型的问题

2. 布隆过滤器

提出背景

用哈希表存储 缺点：浪费空间

用位图存储 缺点： 位图一般只能处理整形，若为字符串，则无法处理
将哈希与位图结合 即布隆过滤器

概念

用多个哈希函数，将一个数据映射到位图结构中
既可以提升效率，又可以节省大量空间

---

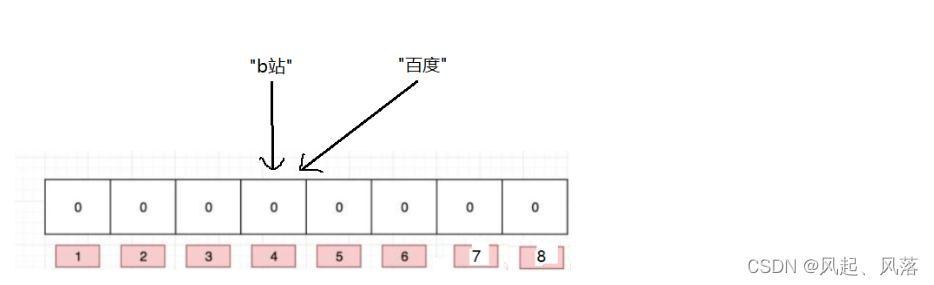
假设两个字符串映射到同一个位置，则会导致哈希冲突
布隆过滤器 想要 降低冲突概率
一个值映射到一个位置，容易误判，一个值映射到多个位置，就可以降低误判率

---

使用多种哈希映射算法，映射到不同的位置
如：每个值都映射到2个位置

具体实现

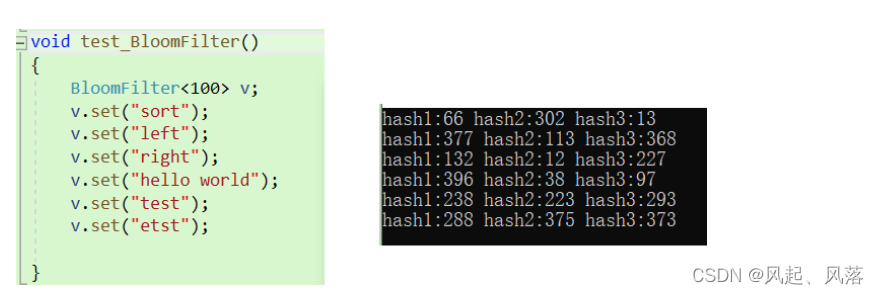
传递模板时，传入hash1 hash2 hash3 ，将K类型转换为整形
hash1 hash2 hash3 作为三种不同的映射方法

hash1 hash2 hash3

BKDRHash算法在哈希中的 针对string情况使用过 ，
当需使用字符串转化为整形时，将字符串中所有字符相加 ，用此确定对应的key
将BKDRHash作为缺省值 ，传给 hash1

点击查看详细解释：哈希

---

将APHash作为缺省值 ，传给hash2

---

将DJBHash作为缺省值 ，传给hash3

---

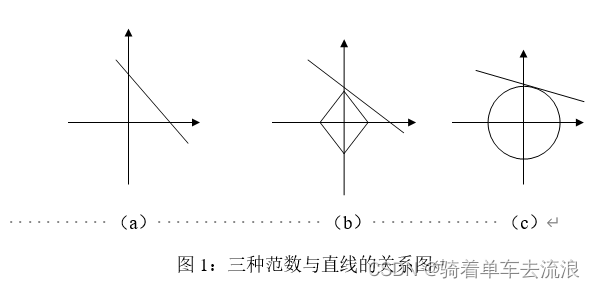
APHash 算法与 DJBHash 算法 是依据数学推导而来的
点击链接查看APHash 算法以及 DJBHash 算法的 具体解释: 哈希算法

---

N取值问题

N代表最多插入key数据的个数

---

k为哈希函数个数，m为布隆过滤器长度，n为插入元素个数

当k为3时， 3= ( m/n ) *0.69，m=4.3n
m越等于4n
布隆过滤器的长度 约等于 插入元素个数的4倍

---

set

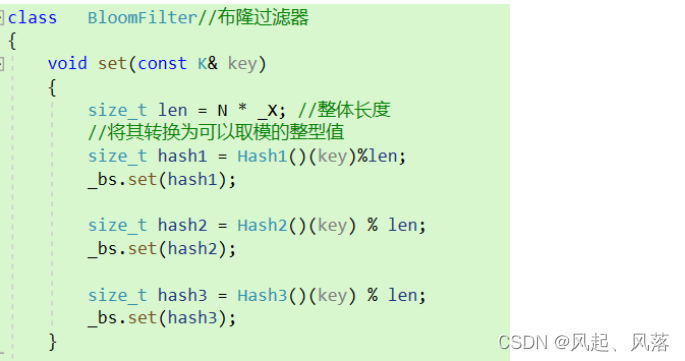
_bs作为题目一的实现的位图结构
通过调用对应hash1 hash2 hash3中的operator() 的不同实现
将传入对应的字符串转换为不同的整形，在使用位图插入在不同的映射位置

---

tset

只有当hash1 hash2 hash3 三个不同的位置都在，它才在，若有一个位置不在，则它就不在

---

就算是两个字符串的ASCII值相同，但是顺序不同，在对应hash1 hash2 hash3 的对应映射位置也是不同的

tset中在与不在那个准确？

不在是准确的，当不在时，当前映射位置为0，若数据存在不可能使映射位置为0

---

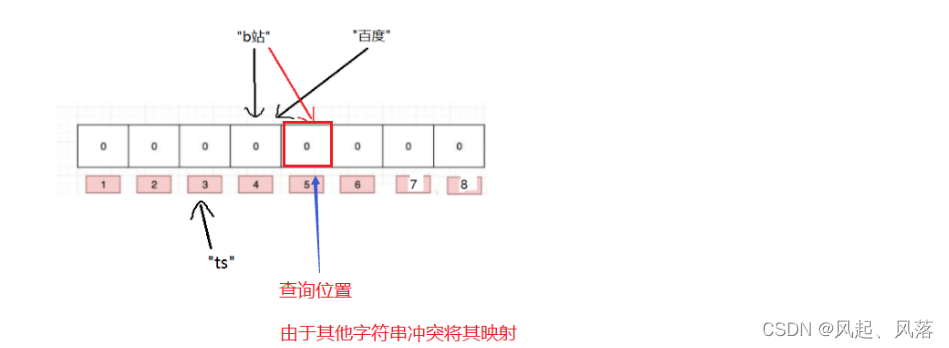
在是不准确的，

ts本来在检查位置是不存在的，但是由于其他字符串发生冲突，正好将其要对ts检查的位置映射了，就会误以为ts存在，导致误判

---

使用场景及特点

能容忍误判的场景
如：快速判断昵称是否使用过
昵称有可能是由于误判，导致可能创建重复的，但是并不会有什么影响存在

---

正常来说，手机号是不能放入布隆过滤器中的，若使用有可能误判， 没有注册过，显示用户存在

但是布隆过滤器也是可以做到的，
若当前数据不在，则直接返回false
若当前数据在，有可能存在误判问题，所以去数据库中查找，若在则直接返回数据存在，若不在，则返回false

---

布隆过滤器的特点
优点：快，节省内存
缺点：存在误判 (数据在)

具体代码

#include<iostream>
using namespace std;
#include<vector>


template<size_t N>
class bitset
{
public:
	bitset()
	{	
		_bits.resize((N / 8) + 1, 0);
	}
	void set(size_t x)
	{
		size_t i = x / 8;//第几个char上
		size_t j = x % 8;//char上的第几个比特位
		_bits[i] |= (1 << j);
	}
	void rset(size_t x)
	{
		size_t i = x / 8;//第几个char上
		size_t j = x % 8;//char上的第几个比特位
		_bits[i] &= ~(1 << j);
	}
	bool test(size_t x)//判断在不在
	{
		size_t i = x / 8;//第几个char上
		size_t j = x % 8;//char上的第几个比特位
		return _bits[i] & (1 << j);
	}
private:
	vector<char> _bits;
};

void test_bitset()
{
	bitset<100> v;
	v.set(10);
	cout << v.test(10) << endl;
	cout << v.test(15) << endl;
}

//仿函数
struct BKDRHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (auto e : s)
		{
			hash += e;
			hash *= 31;
		}
		return hash;
	}
};

struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++)
		{
			size_t ch = s[i];
			if ((i & 1) == 0)
			{

				hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash) << 11) ^ ch ^ (hash >> 5));
			}
		}
		return hash;
	}
};

struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto e : s)
		{
			hash += (hash << 5) + e;
		}
		return hash;
	}
};


template< size_t N,
	class K = string,
	class Hash1 = BKDRHash,
	class Hash2 = APHash,
	class Hash3 = DJBHash>
class	BloomFilter  //布隆过滤器
{
public:
	void set(const K& key)
	{
		size_t len = N * _X; //整体长度
		//将其转换为可以取模的整型值
		size_t hash1 = Hash1()(key) % len;
		_bs.set(hash1);

		size_t hash2 = Hash2()(key) % len;
		_bs.set(hash2);

		size_t hash3 = Hash3()(key) % len;
		_bs.set(hash3);
	}

	//判断在不在
	bool test(const K& key)
	{
		size_t len = N * _X; //整体长度

		//三个位置都在才在，有一个位置不在 则不在
		size_t hash1 = Hash1()(key) % len;
		if (!_bs.set(hash1))
		{
			return false;
		}

		size_t hash2 = Hash2()(key) % len;
		if (!_bs.set(hash2))
		{
			return false;
		}

		size_t hash3 = Hash3()(key) % len;
		_bs.set(hash3);
		if (!_bs.set(hash3))
		{
			return false;
		}
		return true;
	}
private:
	static const size_t _X = 4;//整数倍
	bitset<N* _X> _bs;
};

// 一般是字符串才使用 布隆过滤器
// 所以默认使用字符串类型
void test_BloomFilter()
{
	BloomFilter<100> v;
	v.set("sort");
	v.set("left");
	v.set("right");
	v.set("hello world");
	v.set("test");
	v.set("etst");

}