不经意传输(OT)了解

news2025/1/7 7:06:00

概述

OT，不经意传输，常被大量用于安全多方计算中，能够很大程度决定一个SMPC协议的效率。它的核心概念是接收方可以从发送方（持有秘密信息）手中选择性接收自己想要的信息而接收方对所选择的信息内容一无所知。目前有2-选-1 OT及其扩展OTE（用于PSI，SMPC）和n-选-1 OT及其扩展OTE（PSI，SPIR，不经意采样，不经意多项式求值等等）

Base OT

即，基于公钥密码学的基础 2-选-1 OT协议
半诚实模型
首先假设存在一个公钥加密方案，可以在不获得对应私钥的条件下采样得到一个随机的公钥，经典原语如图

发送方 $S$ 持有秘密消息 $x_1,x_2$ ，而接收方 $R$ 则进行选择。现在来理解一下，首先发送方 $S$ 只能看到由 $R$ 发过来的两个公钥，显然 $S$ 是没办法以超过 $\frac 1 2$ 概率来预测出 $R$ 私钥所对应的公钥的。接着 $R$ 只能看到两个 $S$ 发过来的两个密文，但私钥只能解开其中一个密文。
当然值得注意的是，这只能保证在诚实好奇模型下的安全性，无法抵御恶意。假如恶意的 $R$ 简单生成两对公私钥发送给 $S$ ，那就可以解密得到 $S$ 的两个秘密了。

OTE

即扩展OT协议
在前面的Base OT中，对于每一个选择比特都需要进行一次公钥密码操作，计算量有些大，那么是否有方法能够降低大量执行OT协议时所需要的公钥密码操作数量呢？这就需要提到OTE了，这是一种OT扩展技巧，将伪随机生成器与OT结合，只需要执行少量公钥密码操作，配合上高效的对称密码学，即可产生多项式数量级个大量的OT协议，并且可以保证在诚实好奇模型下的安全。

Beaver的非黑盒构造

基于Yao的混淆电路。下面将混淆电路中的生成方称为发送方 $S$ ，计算方称为 $R$ ，我们知道计算方要完成计算需要利用OT找生成方拿到密钥，假定 $R$ 的选择输入比特为 $m$ ，那么这个GC电路就需要 $m$ 个OT协议。
这里令 $S$ 持有的秘密值为 $(x_1^0,x_1^1),\dots,(x_m^0,x_m^1)$ 共 $m$ 对， $R$ 的输入比特是 $m$ bits的选择比特串 $(b_1,\dots,b_m)$
核心如下
一个功能函数电路 $F$ ，输入是来自 $R$ 的少量比特串，输出多项式数量级的OT协议执行结果。
$R$ 输入的是随机选择的 $k$ 比特字符串 $r$ ，令 $G$ 为一个伪随机生成器，功能是将随机选择的 $k$ 比特字符串扩展到 $m$ 比特长（ $k << m$ ）
步骤如下

首先， $R$ 向 $S$ 发送用随机生成字符串 $G (r)$ 加密的输入比特串 $\oplus G(r)$
$S$ 给功能函数 $F$ 提供输入为 $(x_1^0,x_1^1),\dots,(x_m^0,x_m^1)$ 共 $m$ 对秘密值以及一个 $m$ 比特长度的字符串 $\oplus G(r)$
$R$ 提供给功能函数 $F$ 输入为 $r$ ， $F$ 将计算 $m$ 比特长度的字符串 $G (r)$ ，并解密 $\oplus G(r)$ ，得到选择字符串 $b$
最后 $F$ 向 $R$ 输出 $b_i$ 对应的秘密值 $x_{b_i}$

可以看到 $R$ 只需要提供 $k$ 比特常数长度的输入，即可扩展实现 $m$ 个OT协议。
（吐槽：感觉怪怪的，随机输入的 $r$ 实际上起到的作用貌似就是个 $b$ 的掩码？）
BUT，这个协议很低效，要对一个很大的GC电路进行求值。那么如何提升效率呢？

IKNP[03]

目标：基于少量的 $k$ 个基础OT协议，应用对称密码学操作实现 $m >> k$ 个有效OT扩展协议。
具体步骤如下

假设接收方 $R$ 的选择比特串为 $\in \{0,1\}^m$ ， $R$ 选择两个 $\times k$ 的矩阵 $T, U$ 。令 $t_j,u_j \in \{0,1\}^k$ 标识两个矩阵的行向量，矩阵的元素都是随机选择的，需要满足

$t_j \oplus u_j = r_j \cdot 1^k \stackrel{def}{\longrightarrow} \begin{cases} 1^k, \quad if \ r_j = 1\\ 0^k, \quad if \ r_j = 0 \end{cases}$
这条件的大概意思是，把 $R$ 选的这个选择比特串进行**重复编码，**也就是把这个 $r$ 看作一个列向量，然后重复copy到 $k$ 列，构成一个 $\times k$ 的矩阵，然后拆分成 $T, U$ 两个矩阵，它们的异或结果就是重复编码的矩阵。
借用一个图来表示就是，

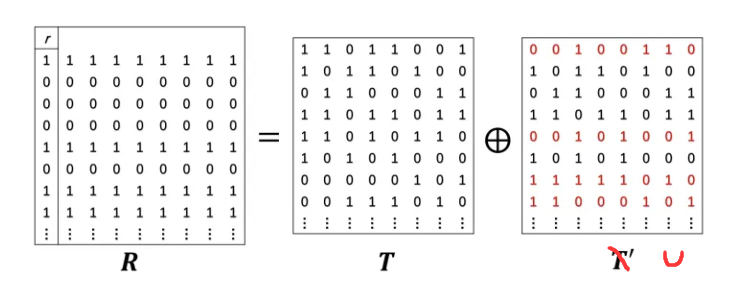
发送方 $S$ 选择随机字符串 $s=\{0,1\}^k$ ，接着调换双方的角色，调用 $k$ 个2选1-OT，接收方 $R$ 根据 $s$ 的各个比特值 $s_i$ 向发送方 $S$ 依次发送 $T ， U$ 矩阵的各个列。即 $t^i,u^i$ 表示第 $i$ 列，它们作为OT协议的秘密值，而 $s_i$ 则作为选择比特。

每一列元素有 $m$ 个( $m >> k$ )，在传递消息时，只需要加密发送两个 $m$ 比特长的字符串，然后再用OT传输短字符串的解密密钥，即可完成长消息的传输。
第 $i$ 个OT协议中，输入 $s_i$ ，将得到输出 $q^i \in \{t^i,u^i\}$ 。

然后将发送方 $S$ 获得的列 $q_i$ 拼起来变成一个矩阵 $Q$ ，借用一张图表示，就是长成这样

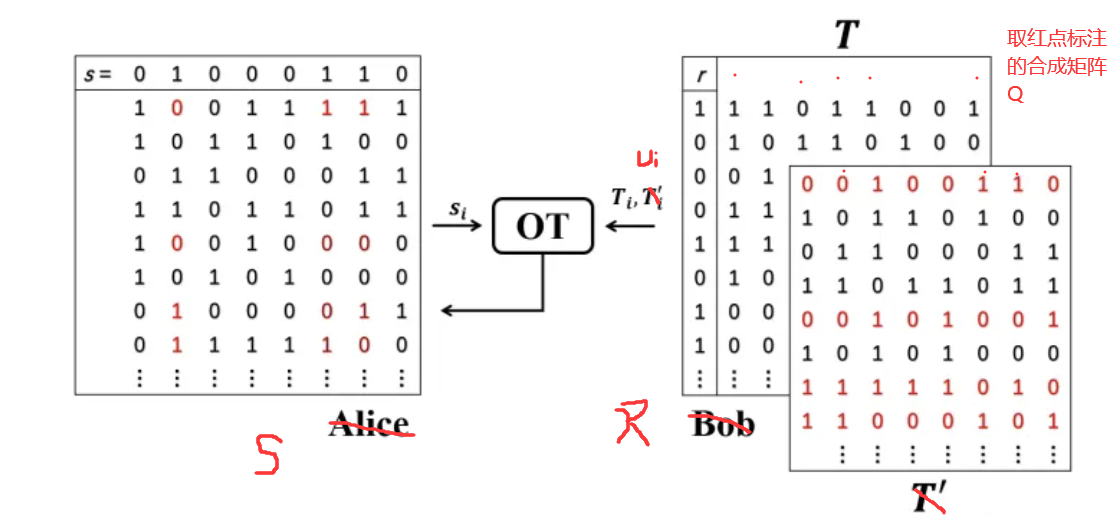
用 $q_j,q^i$ 分别表示矩阵的行和列，观察可以得到，当 $r_j=0$ 时， $q_j = t_j = u_j$ ，而当 $r_j = 1$ 时， $q_j = t_j \oplus s$
进一步结合前面，可以得到一个结论

$q_j = t_j \oplus [r_j \cdot s ]= \begin{cases} t_j, \quad if \ r_j = 0 \\ t_j \oplus s, \quad if \ r_j = 1 \end{cases}$

最后，为了防止 $s$ 重复使用导致消息之间存在一定相关性，采用一个PRG来解决。假定 $H$ 为一个PRG，一个健壮的哈希函数，发送方 $S$ 持有 $s$ 和 $Q$ ，此时就可以计算得到两个随机字符串对 $H(q_j),H(q_j \oplus s)$ ，而接收方 $R$ 持有 $r$ （选择比特）和 $T,t_j$ （随机字符串对之一）,只能通过选择比特计算得到其中一个 $H(t_j)$ 。因此 $m$ 行矩阵的每一行都生成了一个2选1-OT协议，成功传输一个随机字符串。

借用一个图来表示协议内容

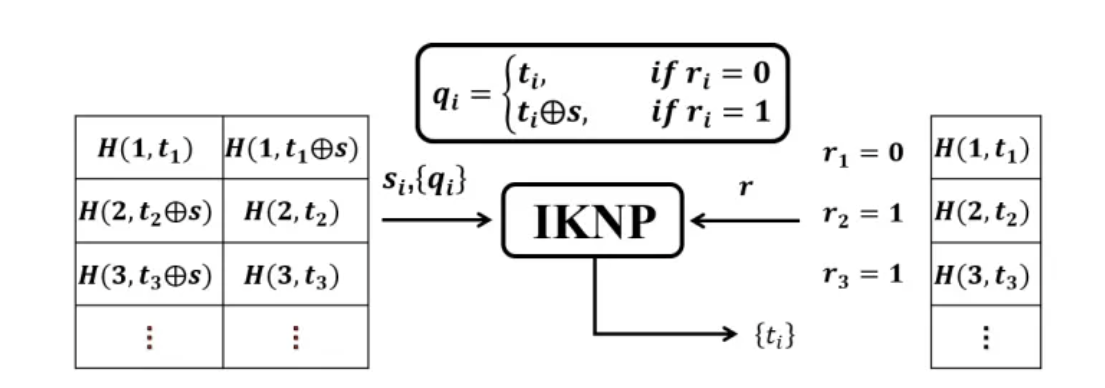
注意到， $q_j$ 的取值取决于接收方 $R$ 的选择比特 $r_j$ ，也能看到整个过程 $R$ 没有得到任何 $s$ 的信息，它只能得到两个随机字符串的其中一个。另外，开始时的Base OT 是按照列进行，共 $k$ 列，所以进行了 $k$ 次，然而每列有 $m$ 个元素，则该协议达成目标：基于少量的 $k$ 个基础OT协议，应用对称密码学操作实现 $m >> k$ 个有效OT扩展协议。
那么这个拿到的随机字符串有啥用？
如果 $S$ 接下来把 $H(q_j)$ 和 $H(q_j \oplus s)$ 这两个看作密钥去加密两个秘密值得到 $H(q_j) \oplus s_0$ 和 $H(q_j \oplus s) \oplus s_1$ 并发送给 $R$ ， $R$ 就可以通过选择比特去拿到关联的秘密值。