前言

上一节，简单概述了树这种数据结构，以及树结构向下，具有某些一些特征的树，比如二叉树，B树，B+树，堆等。其中，二叉树是一个很重要的模块。也是在一些技术面试中，可能会问到的问题。本节，我们就二叉树，做详细介绍。

1. 存储

二叉树是一个逻辑结构，底层可以用数组或者链表存储。

1.1 数组存储

使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来。
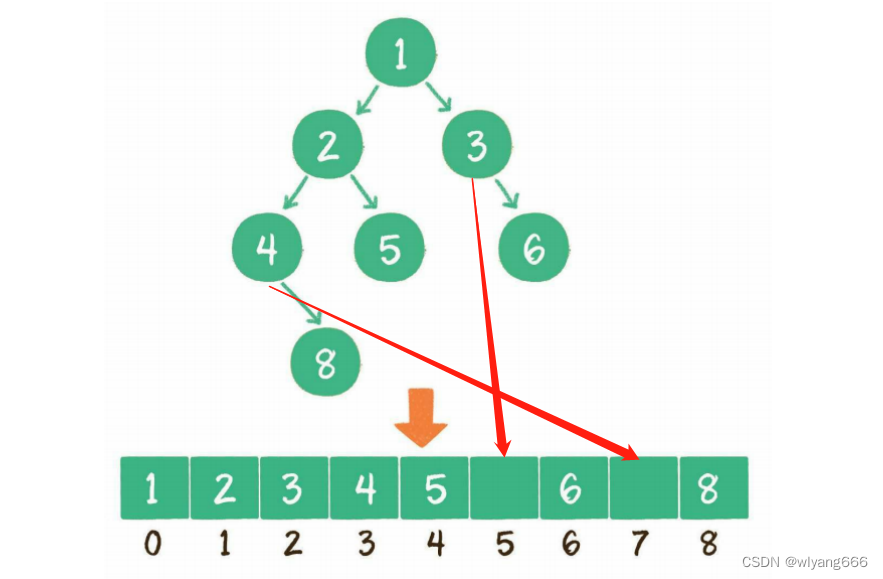
在这里插入图片描述
由此，可以得出结论：在用数组存储时，

一个父节点的下标是n，那么它的左孩子节点下标就是2×n+1、右孩子节点下标就是2x(n+1)
对于一个稀疏的二叉树（孩子不满）来说，用数组表示法是非常浪费空间的
所以二叉树一般用链表存储实现。（二叉堆除外，因为二叉堆是一个完全二叉树，节点基本都是满的）

1.2 链表存储

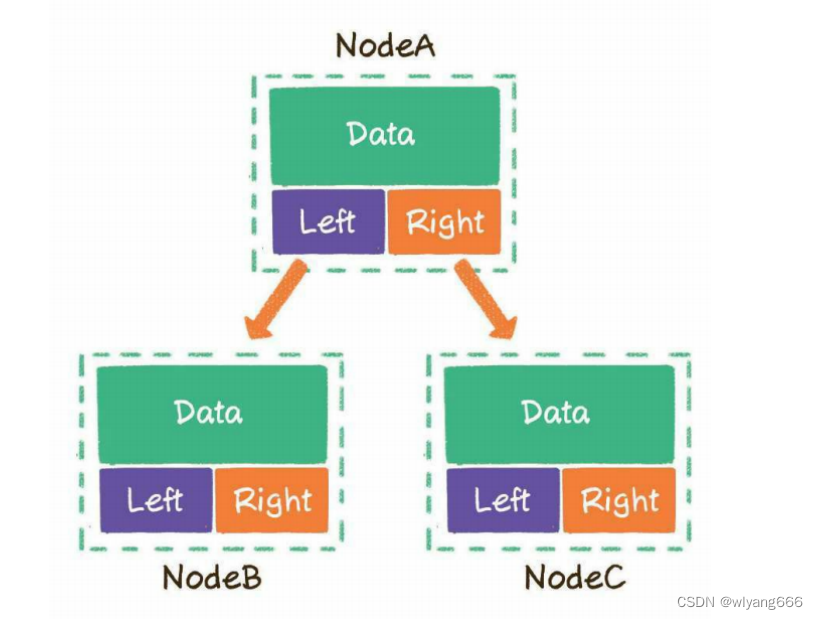
在使用链表存储时，二叉树的每个节点至少包含三部分：

存储数据的data变量
指向左孩子的left指针
指向右孩子的right指针

如下图所示：
在这里插入图片描述

2. 遍历

二叉树，是典型的非线性数据结构，遍历时需要把非线性关联的节点转化成一个线性的序列，以不同的方式来遍历，遍历出的序列顺序也不同。

2.1 深度优先遍历

所谓深度优先，就是偏向于纵深，“一头扎到底”的访问方式。

2.1.1 前序遍历

二叉树的前序遍历，输出顺序是根节点、左子树、右子树。
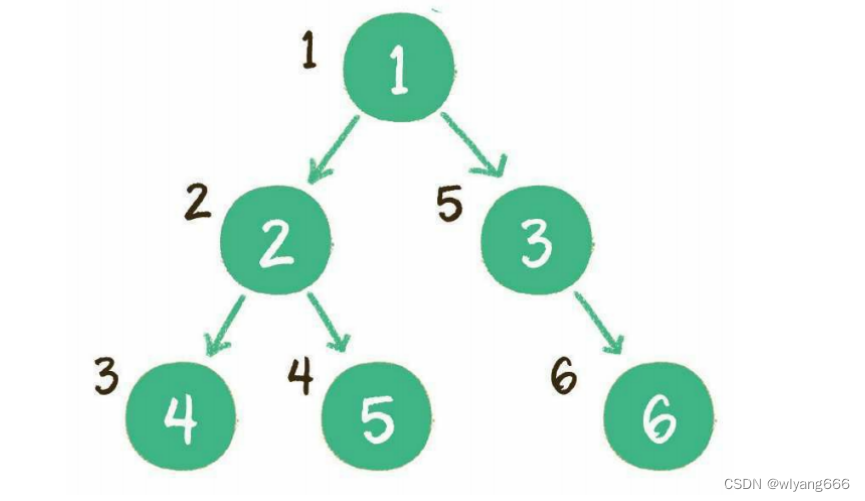
在这里插入图片描述
步骤如下：

首先输出的是根节点1
由于根节点1存在左孩子，输出左孩子节点2
由于节点2也存在左孩子，输出左孩子节点4
节点4既没有左孩子，也没有右孩子，那么回到节点2，输出节点2的右孩子节点5
节点5既没有左孩子，也没有右孩子，那么回到节点1，输出节点1的右孩子节点3
节点3没有左孩子，但是有右孩子，因此输出节点3的右孩子节点6
到此为止，所有的节点都遍历输出完毕

2.1.2 中序遍历

二叉树的中序遍历，输出顺序是左子树、根节点、右子树。
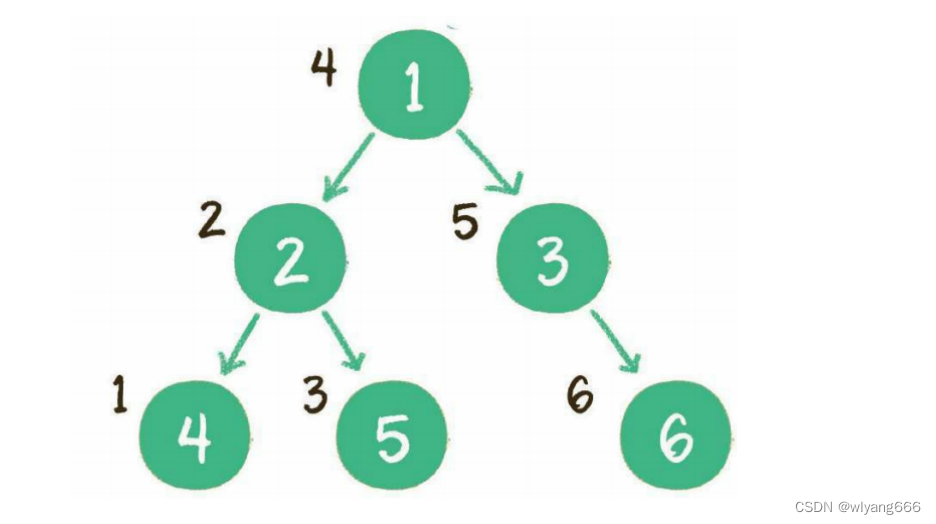
在这里插入图片描述
步骤如下：

首先访问根节点的左孩子，如果这个左孩子还拥有左孩子，则继续深入访问下去，一直找到不再有左孩子的节点，并输出该节点。显然，第一个没有左孩子的节点是节点4
依照中序遍历的次序，接下来输出节点4的父节点2
再输出节点2的右孩子节点5
以节点2为根的左子树已经输出完毕，这时再输出整个二叉树的根节点1
由于节点3没有左孩子，所以直接输出根节点1的右孩子节点3
最后输出节点3的右孩子节点6
到此为止，所有的节点都遍历输出完毕

2.1.3 后序遍历

二叉树的后序遍历，输出顺序是左子树、右子树、根节点
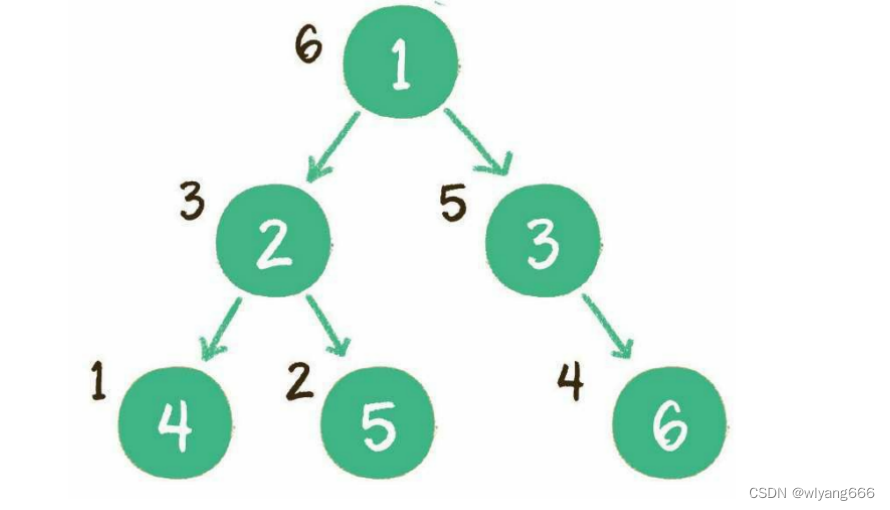
在这里插入图片描述
步骤如下：

首先访问根节点的左孩子，如果这个左孩子还拥有左孩子，则继续深入访问下去，一直找到不再有左孩子的节点，并输出该节点。显然，第一个没有左孩子的节点是节点4
输出右节点5
输出节点4的父节点2
以节点2为根的左子树已经输出完毕，这时再输出整个二叉树的右子树
访问根节点的右孩子，如果这个右孩子拥有左孩子，则继续深入访问下去，一直找到不再有左
孩子的节点，如果没有左孩子则找右孩子，并输出该节点6
输出节点6的父节点3
到此为止，所有的节点都遍历输出完毕。

2.2 广度优先遍历

也叫层序遍历，顾名思义，就是二叉树按照从根节点到叶子节点的层次关系，一层一层横向遍历各个节点。
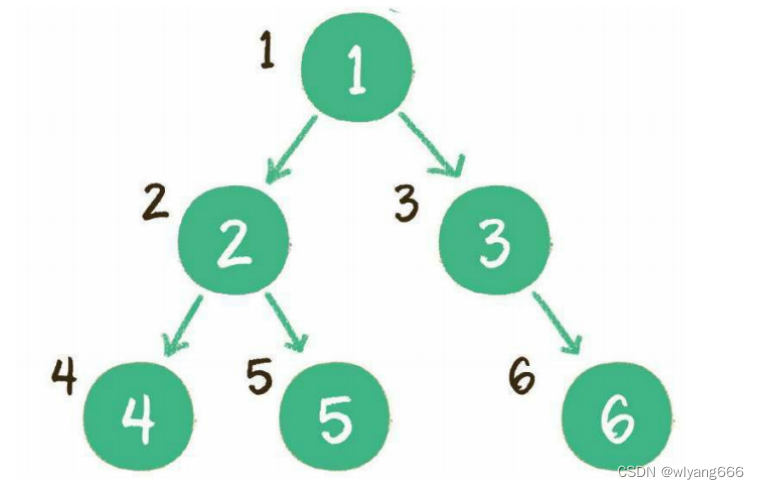
在这里插入图片描述
二叉树同一层次的节点之间是没有直接关联的，利用队列可以实现

2.3 遍历代码实现

2.3.1 定义树节点

package org.wanlong.tree;

/**
 * @author wanlong
 * @version 1.0
 * @description: 树节点定义
 * @date 2023/6/1 11:22
 */
public class TreeNode<T> {
    //数据
    T data;
    //左孩子
    TreeNode left;
    //右孩子
    TreeNode right;


    public TreeNode(T data) {
        this.data = data;
    }
}

2.3.2 定义树节点维护方法

package org.wanlong.tree;

/**
 * @author wanlong
 * @version 1.0
 * @description: 二叉树
 * @date 2023/6/1 11:24
 */
public class BinaryTree {

    TreeNode root;

    public void insertNode(int data) {
        root = insert(root, data);
    }

    /**
     * @param node: 基准节点
     * @param data: 待插入数据
     * @return org.wanlong.tree.TreeNode
     * @Description:往一个节点下面插入data数据
     * @Author: wanlong
     * @Date: 2023/6/1 11:28
     **/
    public TreeNode insert(TreeNode<Integer> node, Integer data) {
        //如果基准节点为空，创建新的节点插入
        if (node == null) {
            return new TreeNode(data);
        }
        //如果待插入数据小于当前节点，插入左子树
        if (data < node.data) {
            //递归确定插入左子树的位置，插入后，返回左子树指针
            node.left = insert(node.left, data);
            //如果待插入节点大于当前节点，插入右子树
        } else if (data > node.data) {
            node.right = insert(node.right, data);
        } else {
            node.data = data;
        }
        return node;
    }
}

2.3.3 前序遍历代码实现

/**
 * @param node:
 * @return void
 * @Description: 前序遍历节点 先根，再左再右
 * @Author: wanlong
 * @Date: 2023/6/1 11:38
 **/
public void preOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    System.out.println(node.data);
    preOrder(node.left);
    preOrder(node.right);
}

2.3.4 中序遍历代码实现

/**
 * @param node:
 * @return void
 * @Description:中序遍历 先左 再根 再右
 * @Author: wanlong
 * @Date: 2023/6/1 11:41
 **/
public void middleOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    middleOrder(node.left);
    System.out.println(node.data);
    middleOrder(node.right);
}

2.3.5 后序遍历代码实现

/**
 * @param node:
 * @return void
 * @Description:后序遍历 先左，再右，再根
 * @Author: wanlong
 * @Date: 2023/6/1 15:21
 **/
public void postOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    postOrder(node.left);
    postOrder(node.right);
    System.out.println(node.data);
}

2.3.6 广度优先遍历代码实现

广度优先遍历可用节点入队出队的方式便捷实现，具体代码实现如下

/**
 * @Description: 广度优先遍历
 * @Author: wanlong
 * @Date: 2023/6/1 15:29
 * @param root:
 * @return void
 **/
public void wideOrder(TreeNode root){
    //广度优先遍历可用队列出队入队的方式快速实现
    LinkedList<TreeNode> queue = new LinkedList<>();
    //根节点入队
    queue.offer(root);
    while (!queue.isEmpty()){
        //队列头节点出队
        TreeNode node = queue.poll();
        //打印数据
        System.out.println(node.data);
        //左右节点入队
        if (node.left!=null){
            queue.offer(node.left);
        }
        if (node.right!=null){
            queue.offer(node.right);
        }
    }
}

2.3.7 遍历结果测试

package org.wanlong.tree;

import org.junit.BeforeClass;
import org.junit.Test;

/**
 * @author wanlong
 * @version 1.0
 * @description: 测试树的遍历
 * @date 2023/6/1 15:15
 */
public class Client {

    static BinaryTree btt = new BinaryTree();

    @BeforeClass
    public static void init() {
        btt.insertNode(10);
        btt.insertNode(8);
        btt.insertNode(11);
        btt.insertNode(7);
        btt.insertNode(9);
        btt.insertNode(12);

    }

    @Test
    public void testpre() {
        btt.preOrder(btt.root);
        //10
        //8
        //7
        //9
        //11
        //12
    }

    @Test
    public void testMiddle() {
        btt.middleOrder(btt.root);
        //7
        //8
        //9
        //10
        //11
        //12
    }

    @Test
    public void testpost() {
        btt.postOrder(btt.root);
        //7
        //9
        //8
        //12
        //11
        //10
    }

    @Test
    public void testwide(){
        btt.wideOrder(btt.root);
    }
    //10
    //8
    //11
    //7
    //9
    //12
}