PIP-Net：用于可解释图像分类的基于patch的直观原型

news2024/10/7 16:27:07

文章目录

PIP-Net: Patch-Based Intuitive Prototypes for Interpretable Image Classification
- 摘要
- 本文方法
- - 模型结构
  - Self-Supervised Pre-Training of Prototypes
  - Training PIP-Net
  - Scoring Sheet Reasoning
  - Compact Explanations
- 实验结果

PIP-Net: Patch-Based Intuitive Prototypes for Interpretable Image Classification

摘要

基于原型patch的可解释方法识别图像中的各种成分，以便向人类解释其推理。然而，现有的基于原型的方法可以学习不符合人类视觉感知的原型，即同一个原型可以指代现实世界中的不同概念，使得解释不直观。
本文方法

在设计可解释性原则的驱动下，我们引入了PIP-Net（基于patch的直觉原型网络）：一种可解释的图像分类模型，它以自我监督的方式学习原型零件，更好地与人类视觉相关
PIP-Net可以被解释为稀疏的评分表，其中图像中原型部分的存在为类别添加了证据。
该模型还可以通过说“我以前从未见过这种情况”来放弃对分发数据不足的决定
只使用图像级别的标签，不依赖于任何零件注释
PIP-Net是全局可解释的，因为所学习的原型集显示了模型的整个推理。
一个较小的局部解释将相关原型定位在一张图像中
PIP-Net缩小了潜在空间和像素空间之间的“语义差距”
PIP-Net具有可解释的原型，使用户能够以直观、忠实和语义有意义的方式解释决策过程
代码地址

本文方法

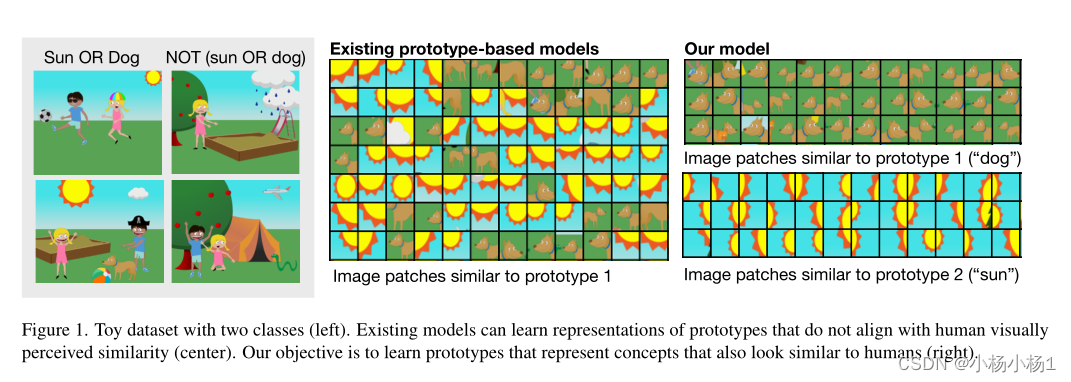
在这里插入图片描述
包含两个类的玩具数据集（左）。现有模型可以学习与人类视觉感知的相似性（中心）不一致的原型的表示。我们的目标是学习代表与人类相似概念的原型（右）。

分类器是基于图像中原型部分的存在的评分表。推理是直观的，因为单对象分类器可以处理多对象图像和分布外数据。因此，我们的模型可以放弃一个决定，而是说“我以前从未见过”。图显示了在PETS（37种猫和狗）上训练的PIP-Net的实际预测和原型位置。
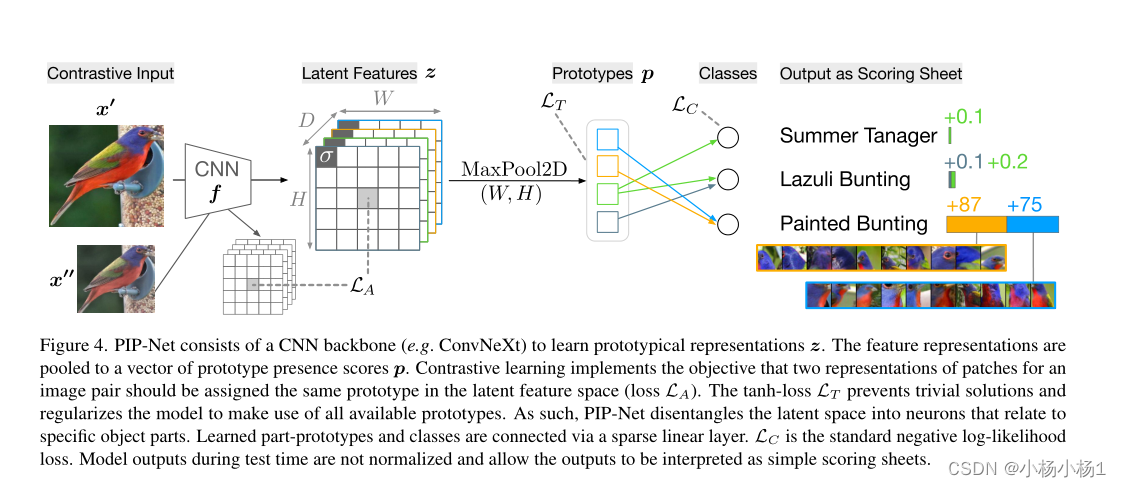
在这里插入图片描述

模型结构

在这里插入图片描述
PIP-Net由CNN主干（例如ConvNeXt）组成，用于学习原型表示z。特征表示被汇集到原型存在分数p的向量中。对比学习实现了一个目标，即图像对的两个patch表示应在潜在特征空间中分配相同的原型（损失LA）。tanh loss LT防止琐碎的解决方案，并正则化模型以利用所有可用的原型。因此，PIP-Net将潜在空间分解为与特定物体部分相关的神经元。学习的零件原型和类通过稀疏线性层连接。LC是标准的负对数似然损失。测试期间的模型输出没有标准化，允许将输出解释为简单的评分表。

Self-Supervised Pre-Training of Prototypes

与对比学习方法类似，我们对表示的对齐和一致性进行了优化。

然而，我们不是在图像级别上优化对齐，而是通过优化模型将相同的原型分配给增强图像补丁的两个视图来优化补丁对齐。具体来说，为了预训练原型，我们只使用两个损失项的线性组合：λALA+λT LT。对准损失LA优化了同一图像块的两个视图，使其属于同一个，理想情况下是单个原型。我们计算图像块（z′h，w，：和z′′h，w，：）的两个视图的潜在块之间的相似性作为它们的点积：
在这里插入图片描述
模型得到LA＝0的一个简单解决方案是让数据集中每个图像中的所有图像块上激活一个原型节点。为了防止这种琐碎的解决方案，并学习利用D原型的整个空间的不同图像表示，我们引入了我们的tanh loss LT，该LT规定每个原型在一个小批量中至少存在一次：
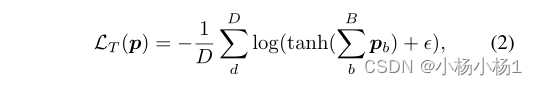
在这里插入图片描述

Training PIP-Net

在对原型进行预训练后，我们解冻最后一个线性层，并将模型作为一个整体进行训练。为了优化分类性能，我们添加了一个分类损失项LC，它简单地是一个标准的负对数似然损失，位于预测和一个热门编码的基本事实标签y之间。LC主要影响线性层的权重，但也微调原型，使其与下游分类任务相关

Scoring Sheet Reasoning

将线性分类层实现为一个可解释的评分表，它在输入样本中寻找（只有积极的）类证据。总结当前原型部分的相关性可以使模型找到多个类别或无类别的证据。
尽管通常使用类置信度分数来训练神经网络，但评分表推理会导致未规范化的输出分数。为了在第二个训练阶段（在原型预训练之后）使用规则的负对数似然损失进行训练，我们在训练期间将softmax激活函数σ应用于线性层o的输出，以将未规范化的logits转换为类置信度得分。

然而，天真地应用softmax将与我们在评分表推理中的紧凑性和决策弃权的目标相冲突，因为softmax不是标度不变的，如果输出分数最初很大（例如，当存在许多具有大权重的类的相关原型时），则softmax输出高度偏斜的分布。

相反当类分数低时（因此当权重或原型存在分数很小时），softmax输出接近均匀分布，例如σ（[0.12，0.65，0.21]）=[0.26，0.45，0.29]。

Compact Explanations

softmax的过度自信也会与我们的紧凑目标相竞争。考虑以下三类场景中的激活示例：σ（[1.2，6.5，2.1）]=[0.005，0.983，0.012]。第二类的置信度分数已经接近1，因此模型没有动机进一步降低其他类的输出分数。原型实际上与类无关，因此可能保持正权重，这会导致解释超出必要范围。原型和类之间的稀疏权重将提高可解释性，因为每个类的相关原型数量和解释大小都减少了。

现有的稀疏性和修剪方法主要是为了降低内存和计算成本而开发的，通常稀疏率必须由用户预先确定，这使得它们与我们的可解释性目标没有直接关系（在增刊中进一步讨论）。相反，我们引入了一种新的函数，可以同时优化分类性能和紧凑性。
为了在训练过程中正则化稀疏性，我们计算输出分数o，用作softmax的输入，如下所示
在这里插入图片描述