cuda编程学习——CUDA共享内存性能优化（九）

news2024/11/27 2:49:07

前言

参考资料：

高升博客
《CUDA C编程权威指南》
以及 CUDA官方文档
CUDA编程：基础与实践 樊哲勇

文章所有代码可在我的GitHub获得，后续会慢慢更新

文章、讲解视频同步更新公众《AI知识物语》，B站：出门吃三碗饭

1：共享内存

共享内存是 一种可被程序员直接操控的缓存，主要作用有两个：
（1）一个是减少核函数中对全局内存的访问次数，实现高效的线程块内部的通信；
（2）一个是提高全局内存访问的合并度。

下面是用C++写的一个归约计算
有 N 个元素的数组 x，假如我们需要计算该数组中所有元素的和，
即 sum = x[0] + x[1] + … + x[N - 1]

#include<stdint.h>
#include<cuda.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <stdio.h>
#include <math.h>
#include <stdio.h>

#define CHECK(call)                                   \
do                                                    \
{                                                     \
    const cudaError_t error_code = call;              \
    if (error_code != cudaSuccess)                    \
    {                                                 \
        printf("CUDA Error:\n");                      \
        printf("    File:       %s\n", __FILE__);     \
        printf("    Line:       %d\n", __LINE__);     \
        printf("    Error code: %d\n", error_code);   \
        printf("    Error text: %s\n",                \
            cudaGetErrorString(error_code));          \
        exit(1);                                      \
    }                                                 \
} while (0)



#ifdef USE_DP
typedef double real;
#else
typedef float real;
#endif

const int NUM_REPEATS = 20;
void timing(const real* x, const int N);
real reduce(const real* x, const int N);

int main(void)
{
    const int N = 100000000;
    const int M = sizeof(real) * N;
    real* x = (real*)malloc(M);
    for (int n = 0; n < N; ++n)
    {
        x[n] = 1.23;
    }

    timing(x, N);

    free(x);
    return 0;
}

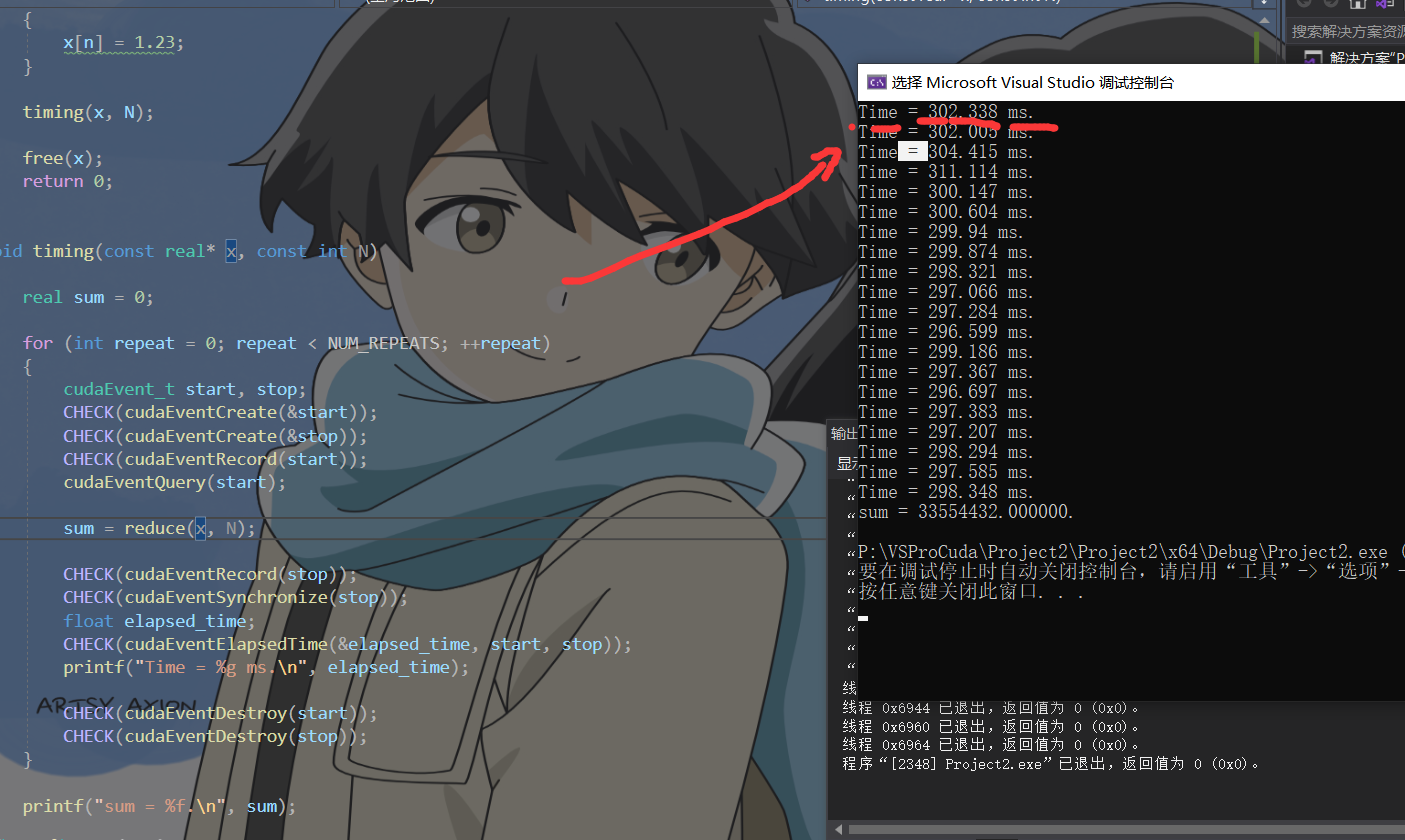
void timing(const real* x, const int N)
{
    real sum = 0;

    for (int repeat = 0; repeat < NUM_REPEATS; ++repeat)
    {
        cudaEvent_t start, stop;
        CHECK(cudaEventCreate(&start));
        CHECK(cudaEventCreate(&stop));
        CHECK(cudaEventRecord(start));
        cudaEventQuery(start);

        sum = reduce(x, N);

        CHECK(cudaEventRecord(stop));
        CHECK(cudaEventSynchronize(stop));
        float elapsed_time;
        CHECK(cudaEventElapsedTime(&elapsed_time, start, stop));
        printf("Time = %g ms.\n", elapsed_time);

        CHECK(cudaEventDestroy(start));
        CHECK(cudaEventDestroy(stop));
    }

    printf("sum = %f.\n", sum);
}

real reduce(const real* x, const int N)
{
    real sum = 0.0;
    for (int n = 0; n < N; ++n)
    {
        sum += x[n];
    }
    return sum;
}

在这里插入图片描述

2：线程同步机制

对于多线程的程序， 两个不同线程中指令的执行次序可能和代码中所展现的次序不同。
要保证核函数中语句的执行顺序与出现顺序一致，就必须使用某种同步机制。 在 CUDA 中，提供了一个同步函数 __syncthreads。该函数只能用在核函数中，其最简单的用法是不带任何参数：
__syncthreads();
该函数可保证一个线程块中的所有线程在执行该语句后面的语句之 前都完全执行了该语句前面的语句。然而，该函数只是针对同一个线程块中的线程的，不同线程块中线程的执行次序依然是不确定的。

3：利用线程同步来归约计算

假如数组元素个数是 2 的整数次方（我们稍后会去掉这个假设），我们可以将数 组后半部分的各个元素与前半部分对应的数组元素相加。如果重复此过程，最后得到的第 一个数组元素就是最初的数组中各个元素的和。这就是所谓的折半归约（binary reduction）法。

3.1 全局内存 条件下的归约计算

void __global__ reduce_global(real* d_x, real* d_y)
{
    const int tid = threadIdx.x;
 //定义指针X，右边表示 d_x 数组第  blockDim.x * blockIdx.x个元素的地址
 //该情况下x 在不同线程块，指向全局内存不同的地址---》使用不同的线程块对dx数组不同部分分别进行处理   
    real* x = d_x + blockDim.x * blockIdx.x;

    //blockDim.x >> 1  等价于 blockDim.x /2，核函数中，位操作比 对应的整数操作高效
    for (int offset = blockDim.x >> 1; offset > 0; offset >>= 1)
    {
        if (tid < offset)
        {
            x[tid] += x[tid + offset];
        }
        //同步语句，作用：同一个线程块内的线程按照代码先后执行指令（块内同步，块外不用同步）
        __syncthreads();
    }

    if (tid == 0)
    {
        d_y[blockIdx.x] = x[0];
    }
}

3.2 静态共享内存 条件下的归约计算

void __global__ reduce_shared(real* d_x, real* d_y)
{
    const int tid = threadIdx.x;
    const int bid = blockIdx.x;
    const int n = bid * blockDim.x + tid;
    //定义了共享内存数组 s_y[128]，注意关键词  __shared__
    __shared__ real s_y[128];
    s_y[tid] = (n < N) ? d_x[n] : 0.0;
    __syncthreads();
    //归约计算用共享内存变量替换了原来的全局内存变量。这里也要记住： 每个线程块都对其中的共享内存变量副本进行操作。在归约过程结束后，每一个线程
    //块中的 s_y[0] 副本就保存了若干数组元素的和
    for (int offset = blockDim.x >> 1; offset > 0; offset >>= 1)
    {

        if (tid < offset)
        {
            s_y[tid] += s_y[tid + offset];
        }
        __syncthreads();
    }

    if (tid == 0)
    {
        d_y[bid] = s_y[0];
    }
}

3.3 动态共享内存 条件下的归约计算

在前面的核函数中，我们在定义共享内存数组时指定了一个固定的长度（128） 。 我们的程序假定了这个长度与核函数的执行配置参数 block_size （也就是核函数中 的 blockDim.x）是一样的。如果在定义共享内存变量时不小心把数组长度写错了，就有可能引起错误或者降低核函数性能。

有一种方法可以减少这种错误发生的概率，那就是使用动态的共享内存

  1. 在调用核函数的执行配置中写下第三个参数：
<<<grid_size, block_size, sizeof(real) * block_size>>>
前面2个参数网格大小和线程块大小，
第三个参数就是核函数中每个线程块需要 定义的动态共享内存的字节数
  1. 要使用动态共享内存，还需要改变核函数中共享内存变量的声明方式
extern __shared__ real s_y[];这是动态声明
__shared__ real s_y[128]; 这是静态声明

归约计算程序代码

#include<stdint.h>
#include<cuda.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <stdio.h>
#include <math.h>
#include <stdio.h>

#define CHECK(call)                                   \
do                                                    \
{                                                     \
    const cudaError_t error_code = call;              \
    if (error_code != cudaSuccess)                    \
    {                                                 \
        printf("CUDA Error:\n");                      \
        printf("    File:       %s\n", __FILE__);     \
        printf("    Line:       %d\n", __LINE__);     \
        printf("    Error code: %d\n", error_code);   \
        printf("    Error text: %s\n",                \
            cudaGetErrorString(error_code));          \
        exit(1);                                      \
    }                                                 \
} while (0)

#ifdef USE_DP
typedef double real;
#else
typedef float real;
#endif

const int NUM_REPEATS = 100;
const int N = 100000000;
const int M = sizeof(real) * N;
const int BLOCK_SIZE = 128;

void timing(real* h_x, real* d_x, const int method);

int main(void)
{
    real* h_x = (real*)malloc(M);
    for (int n = 0; n < N; ++n)
    {
        h_x[n] = 1.23;
    }
    real* d_x;
    CHECK(cudaMalloc(&d_x, M));

    printf("\nUsing global memory only:\n");
    timing(h_x, d_x, 0);
    printf("\nUsing static shared memory:\n");
    timing(h_x, d_x, 1);
    printf("\nUsing dynamic shared memory:\n");
    timing(h_x, d_x, 2);

    free(h_x);
    CHECK(cudaFree(d_x));
    return 0;
}

void __global__ reduce_global(real* d_x, real* d_y)
{
    const int tid = threadIdx.x;
 //定义指针X，右边表示 d_x 数组第  blockDim.x * blockIdx.x个元素的地址
 //该情况下x 在不同线程块，指向全局内存不同的地址---》使用不同的线程块对dx数组不同部分分别进行处理   
    real* x = d_x + blockDim.x * blockIdx.x;

    //blockDim.x >> 1  等价于 blockDim.x /2，核函数中，位操作比 对应的整数操作高效
    for (int offset = blockDim.x >> 1; offset > 0; offset >>= 1)
    {
        if (tid < offset)
        {
            x[tid] += x[tid + offset];
        }
        //同步语句，作用：同一个线程块内的线程按照代码先后执行指令（块内同步，块外不用同步）
        __syncthreads();
    }

    if (tid == 0)
    {
        d_y[blockIdx.x] = x[0];
    }
}

void __global__ reduce_shared(real* d_x, real* d_y)
{
    const int tid = threadIdx.x;
    const int bid = blockIdx.x;
    const int n = bid * blockDim.x + tid;
    //定义了共享内存数组 s_y[128]，注意关键词  __shared__
    __shared__ real s_y[128];
    //将全局内存中的数据复制到共享内存中
    //共享内存的特 征：每个线程块都有一个共享内存变量的副本
    s_y[tid] = (n < N) ? d_x[n] : 0.0;
    //调用函数 __syncthreads 进行线程块内的同步
    __syncthreads();
    //归约计算用共享内存变量替换了原来的全局内存变量。这里也要记住： 每个线程块都对其中的共享内存变量副本进行操作。在归约过程结束后，每一个线程
    //块中的 s_y[0] 副本就保存了若干数组元素的和
    for (int offset = blockDim.x >> 1; offset > 0; offset >>= 1)
    {

        if (tid < offset)
        {
            s_y[tid] += s_y[tid + offset];
        }
        __syncthreads();
    }

    if (tid == 0)
    {
        d_y[bid] = s_y[0];
    }
}

void __global__ reduce_dynamic(real* d_x, real* d_y)
{
    const int tid = threadIdx.x;
    const int bid = blockIdx.x;
    const int n = bid * blockDim.x + tid;
    //声明 动态共享内存 s_y[]  限定词 extern，不能指定数组大小
    extern __shared__ real s_y[];
    s_y[tid] = (n < N) ? d_x[n] : 0.0;
    __syncthreads();

    for (int offset = blockDim.x >> 1; offset > 0; offset >>= 1)
    {

        if (tid < offset)
        {
            s_y[tid] += s_y[tid + offset];
        }
        __syncthreads();
    }

    if (tid == 0)
    {//将每一个线程块中归约的结果从共享内存 s_y[0] 复制到全局内 存d_y[bid]
        d_y[bid] = s_y[0];
    }
}

real reduce(real* d_x, const int method)
{
    int grid_size = (N + BLOCK_SIZE - 1) / BLOCK_SIZE;
    const int ymem = sizeof(real) * grid_size;
    const int smem = sizeof(real) * BLOCK_SIZE;
    real* d_y;
    CHECK(cudaMalloc(&d_y, ymem));
    real* h_y = (real*)malloc(ymem);

    switch (method)
    {
    case 0:
        reduce_global << <grid_size, BLOCK_SIZE >> > (d_x, d_y);
        break;
    case 1:
        reduce_shared << <grid_size, BLOCK_SIZE >> > (d_x, d_y);
        break;
    case 2:
        reduce_dynamic << <grid_size, BLOCK_SIZE, smem >> > (d_x, d_y);
        break;
    default:
        printf("Error: wrong method\n");
        exit(1);
        break;
    }

    CHECK(cudaMemcpy(h_y, d_y, ymem, cudaMemcpyDeviceToHost));

    real result = 0.0;
    for (int n = 0; n < grid_size; ++n)
    {
        result += h_y[n];
    }

    free(h_y);
    CHECK(cudaFree(d_y));
    return result;
}

void timing(real* h_x, real* d_x, const int method)
{
    real sum = 0;

    for (int repeat = 0; repeat < NUM_REPEATS; ++repeat)
    {
        CHECK(cudaMemcpy(d_x, h_x, M, cudaMemcpyHostToDevice));

        cudaEvent_t start, stop;
        CHECK(cudaEventCreate(&start));
        CHECK(cudaEventCreate(&stop));
        CHECK(cudaEventRecord(start));
        cudaEventQuery(start);

        sum = reduce(d_x, method);

        CHECK(cudaEventRecord(stop));
        CHECK(cudaEventSynchronize(stop));
        float elapsed_time;
        CHECK(cudaEventElapsedTime(&elapsed_time, start, stop));
        printf("Time = %g ms.\n", elapsed_time);

        CHECK(cudaEventDestroy(start));
        CHECK(cudaEventDestroy(stop));
    }

    printf("sum = %f.\n", sum);
}

结果比较：
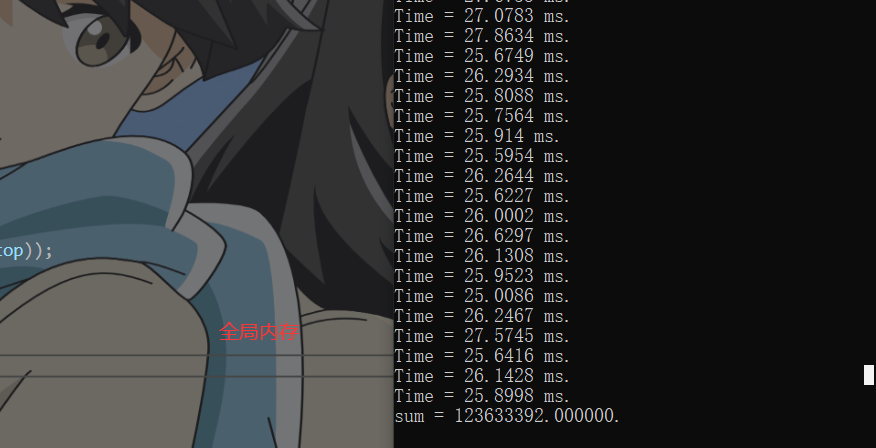
全局内存，耗时25ms，计算结果错误，应该为1.23*10^8，这里后面有很多小数
在这里插入图片描述
静态共享内存，耗时28ms，结果也wrong
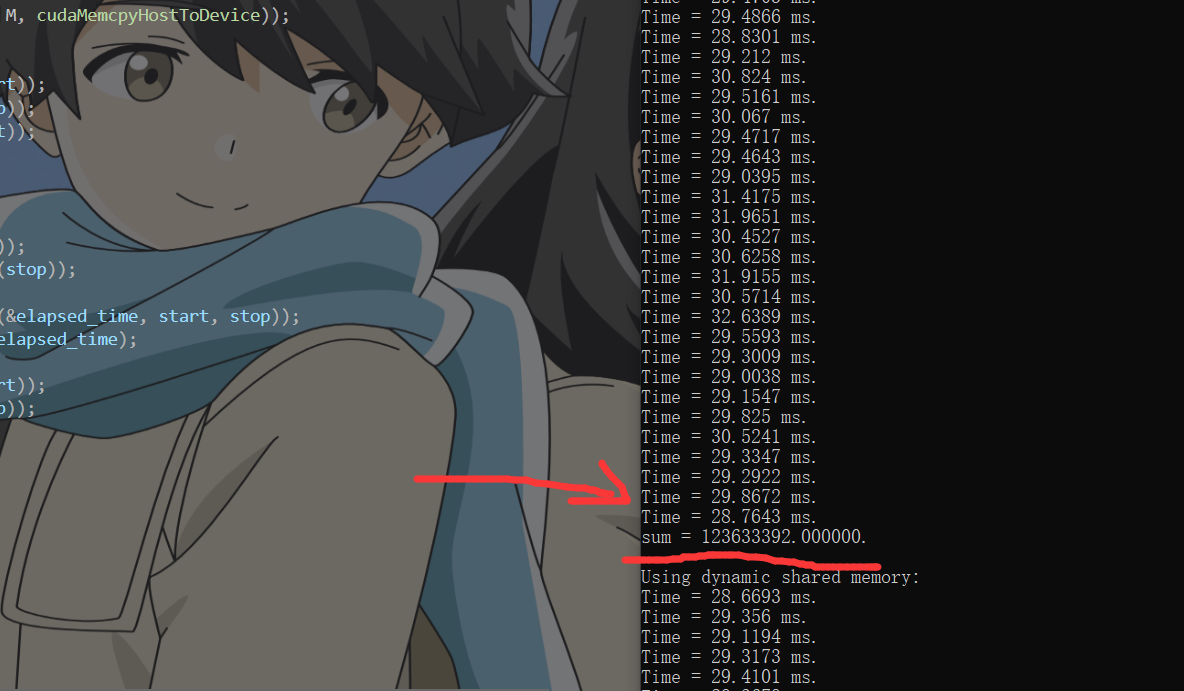
在这里插入图片描述

动态共享内存
耗时29ms
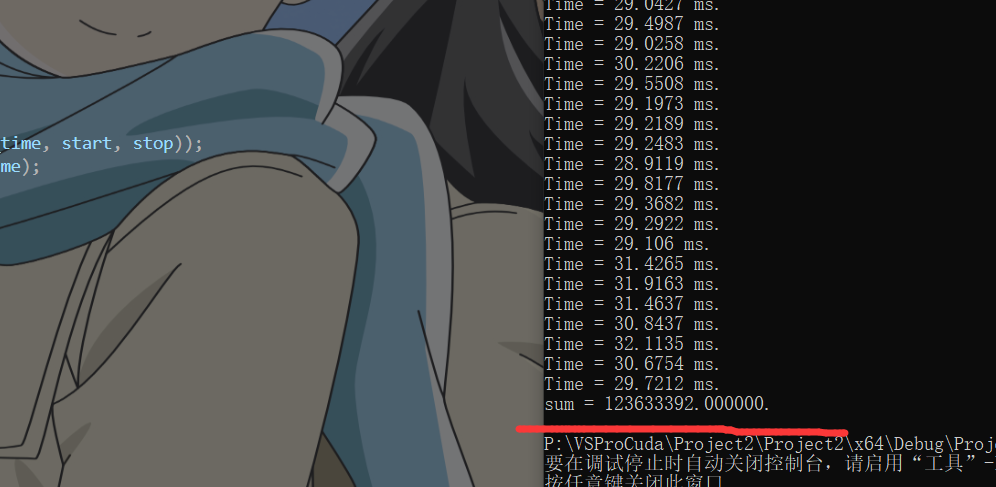
在这里插入图片描述
结论：
（1）全局内存的访问速度是所有内存中最低的，应该尽量减少对它的使用。所有设备内存中，寄 存器是最高效的，但在需要线程合作的问题中，用仅对单个线程可见的寄存器是不够的。我们需要使用对整个线程块可见的共享内存。
（2）使用动态共享内存的核函数和使用静态共享内存的核函 数在执行时间上几乎没有差别。所以，使用动态共享内存不会影响程序性能，但有时可提高程序的可维护性。
（3）使用共享内存来改善全局内存的访问方式并不 一定能够提高核函数的性能。所以，在优化CUDA程序时，一般需要对不同的优化方案进
行测试与比较。
（4）关于计算结果SUM出错，这是因为在累加计算中出现了所谓的“大数吃小数”的现象。单精度浮 点数只有 6、7 位精确的有效数字。在上面的函数 reduce 中，将变量 sum 的值累加到 3000 多万后，再将它和 1.23 相加，其值就不再增加了（小数被大数“吃掉了”，但大数并没有
变化）。
目前的有的解决办法比如： Kahan 求和算法

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/598396.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

绝不可错过！R语言与ggplot2实现SCI论文数据分析神器

绝不可错过！R语言与ggplot2实现SCI论文数据分析神器

一、介绍 1.1 R语言和ggplot2 语言是一种强大的数据分析和统计建模工具&#xff0c;具有广泛的应用领域。 ggplot2是基于R语言的数据可视化工具&#xff0c;具有强大的绘图功能和灵活性。 1.2 数据分析中的重要性 R语言和ggplot2在数据分析中具有广泛的应用&#xff0c;能够帮助…
阅读更多...
有些香港云主机为啥更容易遭遇停机风险？

有些香港云主机为啥更容易遭遇停机风险？

​对于搭建过外贸网站的站长们来说&#xff0c;在面对香港云主机的选择时&#xff0c;往往遇到且出现较为频繁的两个词便是&#xff1a;免费香港云主机和付费香港云主机。其中&#xff0c;一些所谓的免费香港云主机&#xff0c;尤其是长久免费使用&#xff0c;恐怕用户们就要承…
阅读更多...
ES6中函数新增了哪些扩展?

ES6中函数新增了哪些扩展?

参数 &#x1f355;&#x1f355;&#x1f355;ES6允许为函数的参数设置默认值 函数的形参是默认声明的&#xff0c;不能使用let或const再次声明 function foo(x5){let x 1;//errconst x 2;//err }参数默认值可以与解构赋值的默认值结合起来使用 function foo({x,y 5}){co…
阅读更多...
华为OD机试真题B卷 Java 实现【分奖金】，附详细解题思路

华为OD机试真题B卷 Java 实现【分奖金】，附详细解题思路

一、题目描述 公司老板做了一笔大生意&#xff0c;想要给每位员工分配一些奖金&#xff0c;想通过游戏的方式来决定每个人分多少钱。按照员工的工号顺序&#xff0c;每个人随机抽取一个数字。按照工号的顺序往后排列&#xff0c;遇到第一个数字比自己数字大的&#xff0c;那么…
阅读更多...
OpenGL超级宝典第八章学习笔记：基元处理之曲面细分

OpenGL超级宝典第八章学习笔记：基元处理之曲面细分

前言 本篇在讲什么 OpenGL蓝宝书第八章学习笔记之曲面细分 本篇适合什么 适合初学OpenGL的小白 本篇需要什么 对C语法有简单认知 对OpenGL有简单认知 最好是有OpenGL超级宝典蓝宝书 依赖Visual Studio编辑器 本篇的特色 具有全流程的图文教学 重实践&#xff0c;轻…
阅读更多...
CI/CD：如何使用 GitLab 执行 SpringBoot 前后端分离项目的持续集成与持续交付（持续部署）？

CI/CD：如何使用 GitLab 执行 SpringBoot 前后端分离项目的持续集成与持续交付（持续部署）？

一、GitLab Runner 安装 官网各系统 & 各方式安装说明&#xff1a;https://docs.gitlab.com/runner/install/ 本文基于阿里云 CentOS 安装 GitLab Runner &#xff08;Linux Shell 方式&#xff0c;非 Docker 方式&#xff09; 1.1 GitLab Runner 介绍 GitLab Runner 是…
阅读更多...
GPT面试知识点

GPT面试知识点

0.GPT的模型结构 GPT是一个基于Transformer的生成式预训练模型。使用Transformer中的解码器部分 它由一系列的模块化的Transformer Blocks组成。每一个Block包含一个多头自注意力机制(Multi-Head Self-Attention mechanism)以及一个位置前馈网络(position-wise feedforward n…
阅读更多...
Redis - 原理篇

Redis - 原理篇

✨作者&#xff1a;猫十二懿 ❤️‍&#x1f525;账号&#xff1a;CSDN 、掘金 、个人博客 、Github、语雀 &#x1f389;公众号&#xff1a;猫十二懿 Redis(原理篇) 一、数据结构 1.1 动态字符串SDS 我们都知道Redis中保存的Key是字符串&#xff0c;value往往是字符串或者字…
阅读更多...
Spring Boot如何实现分布式锁的自动释放

Spring Boot如何实现分布式锁的自动释放

Spring Boot如何实现分布式锁的自动释放 在分布式系统中&#xff0c;为了保证数据的一致性和可靠性&#xff0c;常常需要使用分布式锁。在实际开发中&#xff0c;我们可以使用 Redis、Zookeeper 等分布式系统来实现分布式锁。本文将介绍如何使用 Spring Boot 来实现分布式锁的…
阅读更多...
Android Input子系统 - kernel

Android Input子系统 - kernel

目录 前言 数据结构 输入子系统流程 前言 上一节有展示Android Input子系统的架构图，这里我们关心Linux kernel层 可以看到kernel层分为三层： 输入子系统设备驱动：处理与硬件相关的信息，调用input API注册输入设备，并把数据往上报 输入子系统核心层：为事件处理层和设…
阅读更多...
关于QGroundControl的软件架构的理解

关于QGroundControl的软件架构的理解

首先QGC是基于QT平台开发&#xff0c;个人理解软件架构即为项目前后端结构&#xff0c;以及前后端数据交互的逻辑。下面是对QGroundControl源码的一些个人理解&#xff0c;写这个博客只是为了记录下来&#xff0c;防止时间久了忘记&#xff0c;过程中看了一些大佬的博客来帮助理…
阅读更多...
服务运营 ｜摘要： Healthcare Management Science 近期论文汇总

服务运营 ｜摘要： Healthcare Management Science 近期论文汇总

推文作者&#xff1a;李舒湉 罗毓灵 编者按 Healthcare Management Science 近期论文汇总 Healthcare Management Science 论文精选&#xff08;三月下&#xff09; 1Monitoring policy in the context of preventive treatment of cardiovascular disease https://link.sprin…
阅读更多...
SQL——视图检查选项 local

SQL——视图检查选项 local

create table stue ( id int auto_increment primary key comment 客户编号, name varchar(20) comment 客户名称, mima varchar(100) comment客户密码 , phonr varchar(20) comment 客户电话, xb char(2) …
阅读更多...
【目录】《电路》上下、《电力电子学》、《数字电路》

【目录】《电路》上下、《电力电子学》、《数字电路》

1、知乎----作为电力电子专业的学生&#xff0c;有哪些专业书籍值得反复阅读&#xff1f; 一门课 / 一本书 经不经典&#xff0c;直接去 中国大学MOOC 上搜一搜就知道了 《电路》 电路主要讲&#xff1a;电压、电阻、电容的一些计算公式 《电力电子学》 https://www.zhih…
阅读更多...
Hexo 搭建博客并推送GitHub

Hexo 搭建博客并推送GitHub

初始Hexo npm install hexo-cli -g hexo init blog cd blog npm install hexo server浏览器访问&#xff1a;http://localhost:4000/ 设置GitHub 1、首先要注册一个Github账号&#xff0c;新建一个name.github.io的仓库&#xff0c;也就是new repository。 因为博主之前创建…
阅读更多...
Sui主网升级至V1.2.0版本

Sui主网升级至V1.2.0版本

升级要点 [API行为调整] — 因rpc方法导致的UserInputError、 SuiRpcInputError、SuiError::TransactionNotFound以及SuiError::TransactionsNotFound报错&#xff0c;现在返回错误代码为32602&#xff0c;取代了32000。此信息已在#11833 #11928中更正。 修复了get_coin_meta…
阅读更多...
Python实战基础18-文件操作

Python实战基础18-文件操作

1、文件的打开和关闭 1.1 操作文件的整体过程 打开文件&#xff0c;或者新建立一个文件读/写数据关闭文件 1.2 打开文件 在python&#xff0c;使用open函数&#xff0c;可以打开一个已经存在的文件&#xff0c;或者创建一个新文件。 open(文件路径&#xff0c;访问模式) …
阅读更多...
【教程】在 Visual Studio 2015 上对 C++ 进行单元测试

【教程】在 Visual Studio 2015 上对 C++ 进行单元测试

更新中 目录 前言环境Visual Studio 2015 提供的单元测试工具创建 C 测试框架在测试项目内测试一个函数测试另一个 Project 的函数参考 前言 本文的测试环境是 Visual Studio 2015&#xff0c;高级别版本&#xff08;如&#xff0c;2017&#xff0c;2022&#xff09;的操作略有…
阅读更多...
SpringBoot + 规则引擎 URule，太强了！

SpringBoot + 规则引擎 URule，太强了！

一、背景 前段时间&#xff0c;在做项目重构的时候&#xff0c;遇到很多地方需要做很多的条件判断。当然可以用很多的if-else判断去解决&#xff0c;但是当时也不清楚怎么回事&#xff0c;就想玩点别的。于是乎&#xff0c;就去调研了规则引擎。 当然&#xff0c;市面上有很多…
阅读更多...
[unity]如何并行for循环

[unity]如何并行for循环

序 并行for循环 计算着色器里可以弄&#xff0c;但是那个得先了解一堆api&#xff0c;比如什么setBuffer unity 的 job system好像也可以弄&#xff0c;但是那个也得先了解一堆api 这些都是大而全的&#xff0c;有没有那种&#xff0c;没那么神通广大但是比较容易上手的&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023