红黑树也是一种自平衡的二叉搜索树，和AVL树比较，插入和删除时，旋转的次数更少。

红黑树的特性：

1. 所有节点都有颜色：红色或者黑色
2. 所有null均视为黑色
3. 红色节点不能相邻
4. 根节点是黑色
5. 从根节点到任意一个叶子节点，路径中的黑色节点数一样（黑色完美平衡）

构造红黑树节点 ---- 初始颜色都为红色

    static class RBNode {
        int key;
        Object value;
        String color = "red";
        RBNode left;
        RBNode right;
        RBNode parent;

        public RBNode(int key, Object value) {
            this.key = key;
            this.value = value;
        }

        // 是否是左孩子
        boolean isLeftChild() {
            return parent != null && parent.left == this;
        }

        // 找到当前节点的叔叔节点
        RBNode uncle() {
            if (parent == null || parent.parent == null) {
                return null;
            }
            if (parent.isLeftChild()) {
                return parent.parent.right;
            } else {
                return parent.parent.left;
            }
        }

        // 找到当前节点的兄弟节点
        RBNode brother() {
            if (parent == null) {
                return null;
            }
            if (this.isLeftChild()) {
                return parent.right;
            } else {
                return parent.left;
            }
        }
    }

红黑树的左旋和右旋：

右旋，如图所示：

 

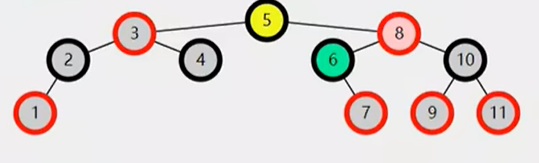
 代码：

参考上图进行理解，相比较AVL树，多了一个parent节点的赋值。

    public void rightRotate(RBNode pink) {
        RBNode parent = pink.parent;
        RBNode yellow = pink.left;
        RBNode green = yellow.right;
        if (green != null) {
            green.parent = pink;
        }
        yellow.right = pink;
        yellow.parent = parent;
        pink.left = green;
        pink.parent = yellow;

        if (parent == null) {
            root = yellow;
        } else if (parent.left == pink) {
            parent.left = yellow;
        } else {
            parent.right = yellow;
        }
    }

    public void leftRotate(RBNode pink) {
        RBNode parent = pink.parent;
        RBNode yellow = pink.right;
        RBNode green = yellow.left;

        if (green != null) {
            green.parent = pink;
        }
        yellow.left = pink;
        yellow.parent = parent;
        pink.right = green;
        pink.parent = yellow;

        if (parent == null) {
            root = yellow;
        } else if (parent.left == pink) {
            parent.left = yellow;
        } else {
            parent.right = yellow;
        }
    }

红黑树的插入操作

红黑树的插入操作，也是遵循平衡二叉树的插入操作的。不同的是，需要维护父亲节点的信息，以及颜色信息。

    public void put(int key, Object value) {
        RBNode node = root;
        RBNode parent = null;
        while (node != null) {
            parent = node;
            if (key < node.key) {
                node = node.left;
            } else if (key > node.key) {
                node = node.right;
            } else {
                node.value = value;
                return;
            }
        }

        RBNode insert = new RBNode(key, value);
        if (parent == null) {
            root = insert;
        } else if (key < parent.key) {
            parent.left = insert;
            insert.parent = parent;
        } else {
            parent.right = insert;
            insert.parent = parent;
        }

        // 调整颜色信息
        fixRedRed(insert);
    }

每次插入操作的时候，都需要维护颜色信息，保证符合红黑树的特性：

1. 插入的节点是根节点 ------ 首次插入节点，直接把根节点变成黑色就可以。
2. 插入的节点父节点是黑色 ------- 树的红黑树性质不会改变，直接插入即可
3. 插入的节点父亲是红色节点 -------- 出现红红相邻的情况，此时就需要调整红黑树了
   1. 叔叔节点是红色 ---  平衡方法如下：
      1. 父亲节点和叔叔节点都变成黑色，祖父节点变成红色
      2. 此时需要调整祖父节点的颜色信息了，其实就是递归调用，传参树祖父节点
   2. 叔叔节点是黑色 --- 四种情况
      1. LL：父亲节点是左孩子，插入的节点也是左孩子
         1. 父节点变黑，祖父节点变红，以祖父节点为根，执行一次右旋操作
      2. LR：父亲节点是左孩子，插入的节点是右孩子
         1. 以父亲节点为根执行一次左旋操作--- 此时得到了LL结构
         2. 新的父亲节点变黑（插入的节点），祖父节点变红，以祖父节点为根，执行一次右旋操作
      3. RR：父亲节点是右孩子，插入的节点也是右孩子
         1. 父节点变黑，祖父节点变红，以祖父节点为根，执行一次左旋操作
      4. RL：父亲节点是右孩子，插入的节点是左孩子
         1. 以父亲节点为根执行一次右旋操作--- 此时得到了RR结构
         2. 新的父亲节点变黑（插入的节点），祖父节点变红，以祖父节点为根，执行一次左旋操作

    private void fixRedRed(RBNode x) {
        // 1、插入的是根节点，变黑返回
        if (x == root) {
            x.color = "black";
            return;
        }
        // 2、父节点为黑色，直接返回
        if (isBlack(x.parent)) {
            return;
        }

        // 父亲节点为红色，红红相邻
        RBNode uncle = x.uncle();
        RBNode parent = x.parent;
        RBNode grandparent = parent.parent;

        //3、叔叔节点是红色
        if (isRed(uncle)) {
            parent.color = "black";
            uncle.color = "black";
            grandparent.color = "red";
            fixRedRed(grandparent);
            return;
        }

        //4、 叔叔节点是黑色 ，
        if (parent.isLeftChild()) { // 父亲左孩子
            if (x.isLeftChild()) { // 插入节点在左边
                // LL
                parent.color = "black";
                grandparent.color = "red";
                rightRotate(grandparent);
            } else { // 插入节点在右边
                // LR
                leftRotate(parent);
                x.color = "black";
                grandparent.color = "red";
                rightRotate(grandparent);
            }
        } else { // 父亲右孩子
            if (!x.isLeftChild()) { // 插入节点在右边
                // RR
                parent.color = "black";
                grandparent.color = "red";
                leftRotate(grandparent);
            } else { // 插入节点在左边
                // RL
                rightRotate(parent);
                x.color = "black";
                grandparent.color = "red";
                leftRotate(grandparent);
            }
        }
    }

红黑树节点的删除

肝不动了，后面在补吧