旅行商问题TSP

news2024/12/25 9:16:14

目录

蚁群算法

Hopfield网络

遗传算法

免疫算法

蚁群算法

求解思路

Hopfield网络

Hopfield网络适合求结果的次优解，可以保证解向能量函数最小值方向收敛，但不能确保达到全局最小点。

实现能量函数

网格能量的最小值对应于最佳或者次最佳的路径距离。

%%%%%%%计算能量函数%%%%%%%%%%%%
function E=energy(V,d) 
global A D
n=size(V,1);
sum_x=sumsqr(sum(V,2)-1);
sum_i=sumsqr(sum(V,1)-1);
V_temp=V(:,2:n);
V_temp=[V_temp V(:,1)];
sum_d=d*V_temp;
sum_d=sum(sum(V.*sum_d));
E=0.5*(A*sum_x+A*sum_i+D*sum_d);

实现动态方程

 repmat - 重复数组副本
    此 MATLAB 函数 返回一个数组，该数组在其行维度和列维度包含 A 的 n 个副本。A 为矩阵时，B 大小为 size(A)*n。

%%%%%%%%%%计算du%%%%%%%%%%%
function du=diu(V,d) 
global A D
n=size(V,1);
sum_x=repmat(sum(V,2)-1,1,n);
sum_i=repmat(sum(V,1)-1,n,1);
V_temp=V(:,2:n);
V_temp=[V_temp V(:,1)];
sum_d=d*V_temp;
du=-A*sum_x-A*sum_i-D*sum_d;

优化计算

clear all
clc 
%定义全局变量
global A D
%导入城市位置
load location
%计算相互城市间距离
distance=dist(citys,citys');
%初始化网络
N=size(citys,1);
A=500;
D=200;
U0=0.2;
step=0.00005;
delta=2*rand(N,N)-1;
U=U0*log(N-1)+delta;
V=(1+tansig(U/U0))/2;
iter_num=5000;
E=zeros(1,iter_num);
%寻优迭代
for k=1:iter_num  
    % 动态方程计算
    dU=diu(V,distance);
    % 输入神经元状态更新
    U=U+dU*step;
    % 输出神经元状态更新
    V=(1+tansig(U/U0))/2;
    % 能量函数计算
    e=energy(V,distance);
    E(k)=e;  
end
 %判断路径有效性
[rows,cols]=size(V);
V1=zeros(rows,cols);
[V_max,V_ind]=max(V);
for j=1:cols
    V1(V_ind(j),j)=1;
end
C=sum(V1,1);
R=sum(V1,2);
flag=isequal(C,ones(1,N)) & isequal(R',ones(1,N));
%结果显示
if flag==1
   % 计算初始路径长度
   sort_rand=randperm(N);
   citys_rand=citys(sort_rand,:);
   Length_init=dist(citys_rand(1,:),citys_rand(end,:)');
   for i=2:size(citys_rand,1)
       Length_init=Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');
   end
   % 绘制初始路径
   figure(1)
   plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')
   for i=1:length(citys)
       text(citys(i,1),citys(i,2),['   ' num2str(i)])
   end
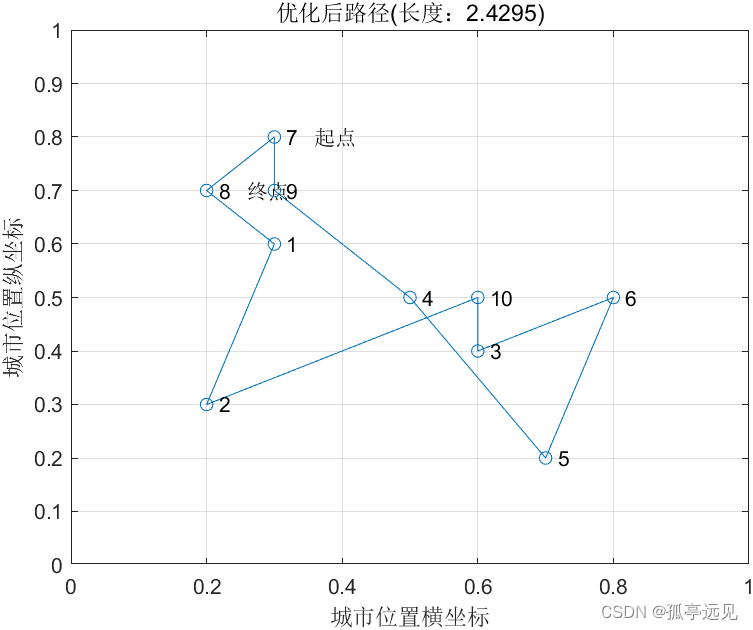
   text(citys_rand(1,1),citys_rand(1,2),['       起点' ])
   text(citys_rand(end,1),citys_rand(end,2),['       终点' ])
   title(['优化前路径(长度：' num2str(Length_init) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 计算最优路径长度
   [V1_max,V1_ind]=max(V1);
   citys_end=citys(V1_ind,:);
   Length_end=dist(citys_end(1,:),citys_end(end,:)');
   for i=2:size(citys_end,1)
       Length_end=Length_end+dist(citys_end(i-1,:),citys_end(i,:)');
   end
  
   % 绘制最优路径
   figure(2)
   plot([citys_end(:,1);citys_end(1,1)],...
       [citys_end(:,2);citys_end(1,2)],'o-')
   for i=1:length(citys)
       text(citys(i,1),citys(i,2),['  ' num2str(i)])
   end
   text(citys_end(1,1),citys_end(1,2),['       起点' ])
   text(citys_end(end,1),citys_end(end,2),['       终点' ])
   title(['优化后路径(长度：' num2str(Length_end) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 绘制能量函数变化曲线
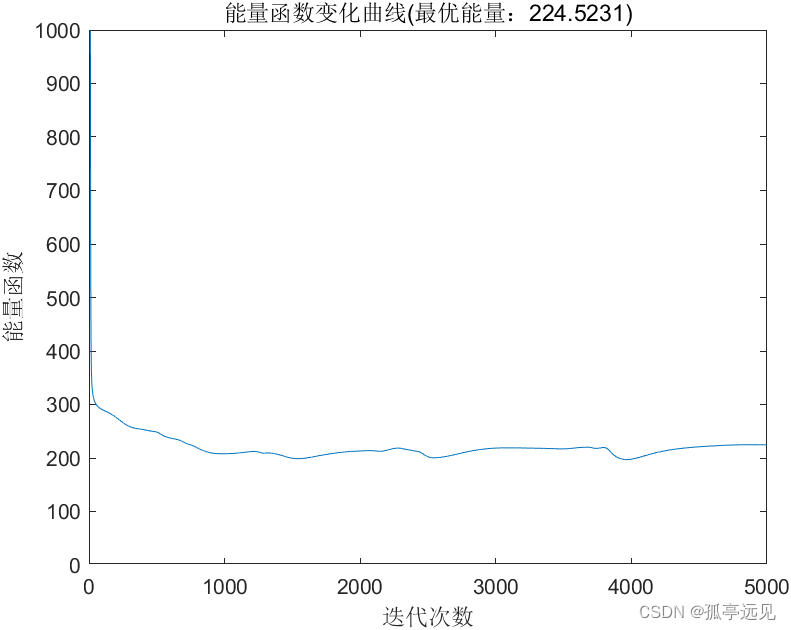
   figure(3)
   plot(1:iter_num,E);
   ylim([0 1000])
   title(['能量函数变化曲线(最优能量：' num2str(E(end)) ')']);
   xlabel('迭代次数');
   ylabel('能量函数');
else
   disp('寻优路径无效');
end

 

遗传算法

 基本步骤

 

 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%主函数%%%%%%%%%%%%%
clear;
clc;
%%%%%%%%%%%%%输入参数%%%%%%%%%%%%
N=10;               %%城市的个数
M=20;               %%种群的个数
C=100;               %%迭代次数
C_old=C;
m=2;                %%适应值归一化淘汰加速指数
Pc=0.8;             %%交叉概率
Pmutation=0.2;       %%变异概率

%%%%%%%%%生成城市的坐标%%%%%%%%%%%%%%%%
pos=randn(N,2);

%%%%%%%%生成城市之间距离矩阵%%%%%%%%%%%%
D=zeros(N,N);
for i=1:N
    for j=i+1:N
        dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2;
        D(i,j)=dis^(0.5);
        D(j,i)=D(i,j);
    end
end

%%%%%%%%生成初始群体%%%%%%%%%%%%%%%%%%%%
popm=zeros(M,N);
for i=1:M
    popm(i,:)=randperm(N);
end

%%%%%%%%随机选择一个种群%%%%%%%%%%%%%%%%
R=popm(1,:);
figure(1);
subplot(2,1,1)
scatter(pos(:,1),pos(:,2),'k.');
xlabel('横轴')
ylabel('纵轴')
title('随机产生的种群图')
axis([-3 3 -3 3]);
subplot(2,1,2)
plot_route(pos,R);      
xlabel('横轴')
ylabel('纵轴')
title('随机生成种群中城市路径情况')
axis([-3 3 -3 3]);

%%%%%%%%初始化种群及其适应函数%%%%%%%%%%%%
fitness=zeros(M,1);
len=zeros(M,1);
for i=1:M
    len(i,1)=myLength(D,popm(i,:));
end
maxlen=max(len);
minlen=min(len);
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
R=popm(rr(1,1),:);
for i=1:N
fprintf('%d ',R(i));
end
fprintf('\n');
fitness=fitness/sum(fitness); 
distance_min=zeros(C+1,1);  %%各次迭代的最小的种群的距离
while C>=0
fprintf('迭代第%d次\n',C);
%%%%选择操作%%%%
nn=0;
for i=1:size(popm,1)
    len_1(i,1)=myLength(D,popm(i,:));
    jc=rand*0.3;
    for j=1:size(popm,1)
        if fitness(j,1)>=jc
        nn=nn+1;
        popm_sel(nn,:)=popm(j,:);
        break;
        end
    end
end
%%%%每次选择都保存最优的种群%%%%
popm_sel=popm_sel(1:nn,:);
[len_m len_index]=min(len_1);
popm_sel=[popm_sel;popm(len_index,:)]; 
%%%%交叉操作%%%%
nnper=randperm(nn);
A=popm_sel(nnper(1),:);
B=popm_sel(nnper(2),:);
for i=1:nn*Pc
[A,B]=cross(A,B);
popm_sel(nnper(1),:)=A;
popm_sel(nnper(2),:)=B;
end
%%%%变异操作%%%%
for i=1:nn
    pick=rand;
    while pick==0
         pick=rand;
    end
    if pick<=Pmutation
       popm_sel(i,:)=Mutation(popm_sel(i,:));
    end
end
%%%%求适应度函数%%%%
NN=size(popm_sel,1);
len=zeros(NN,1);
for i=1:NN
    len(i,1)=myLength(D,popm_sel(i,:));
end
maxlen=max(len);
minlen=min(len);
distance_min(C+1,1)=minlen;
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
fprintf('minlen=%d\n',minlen);
R=popm_sel(rr(1,1),:);
for i=1:N
fprintf('%d ',R(i));
end
fprintf('\n');
popm=[];
popm=popm_sel;
C=C-1;
%pause(1);
end
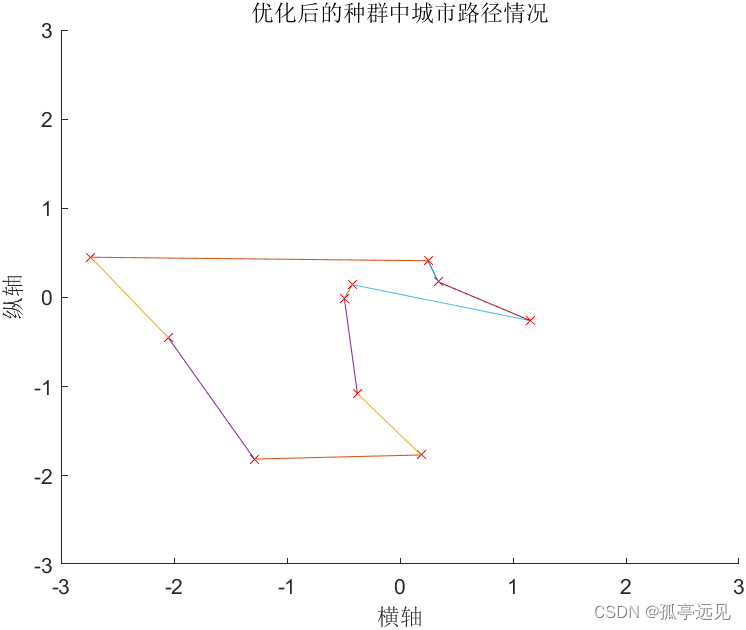
figure(2)
plot_route(pos,R);
xlabel('横轴')
ylabel('纵轴')
title('优化后的种群中城市路径情况')
axis([-3 3 -3 3]);

% %%%%%%%%适应度函数%%%%%%%%%%%%%%%%%%%%
% function fitness=fit(len,m,maxlen,minlen)
%     fitness=len;
%     for i=1:length(len)
%         fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
%     end
% end
% 
% %%%%%%%%个体距离计算函数%%%%%%%%%%%%
% function len=myLength(D,p)
%     [N,NN]=size(D);
%     len=D(p(1,N),p(1,1));
%     for i=1:(N-1)
%         len=len+D(p(1,i),p(1,i+1));
%     end
% end
% 
% %%%%%%%%交叉操作函数%%%%%%%%%%%%%%%%%%%%
% function [A,B]=cross(A,B)
%     L=length(A);
%     if L<10
%         W=L;
%     elseif ((L/10)-floor(L/10))>=rand&&L>10
%         W=ceil(L/10)+8;
%     else
%         W=floor(L/10)+8;
%     end
%     p=unidrnd(L-W+1);
%     fprintf('p=%d ',p);
%     for i=1:W
%         x=find(A==B(1,p+i-1));
%         y=find(B==A(1,p+i-1));
%         [A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
%         [A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
%     end
% end
% 
% %%%%%%%%对调函数%%%%%%%%%%%%%%%%%%%%
% function [x,y]=exchange(x,y)
%     temp=x;
%     x=y;
%     y=temp;
% end
% 
% %%%%%%%%变异函数%%%%%%%%%%%%%%%%%%%%
% function a=Mutation(A)
%     index1=0;index2=0;
%     nnper=randperm(size(A,2));
%     index1=nnper(1);
%     index2=nnper(2);
%     %fprintf('index1=%d ',index1);
%     %fprintf('index2=%d ',index2);
%     temp=0;
%     temp=A(index1);
%     A(index1)=A(index2);
%     A(index2)=temp;
%     a=A;
% end
% 
% %%%%%%%%连点画图函数%%%%%%%%%%%%%%%%%%%%%%%%
% function plot_route(a,R)
%     scatter(a(:,1),a(:,2),'rx');
%     hold on;
%     plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]);
%     hold on;
%     for i=2:length(R)
%         x0=a(R(i-1),1);
%         y0=a(R(i-1),2);
%         x1=a(R(i),1);
%         y1=a(R(i),2);
%         xx=[x0,x1];
%         yy=[y0,y1];
%         plot(xx,yy);
%         hold on;
%     end
% end

 randperm - 整数的随机排列 p = randperm(n)
    此 MATLAB 函数 返回行向量，其中包含从 1 到 n 没有重复元素的整数随机排列。

 scatter - 散点图    scatter(x,y)
    此 MATLAB 函数 在向量 x 和 y 指定的位置创建一个包含圆形标记的散点图。该类型的图形也称为气泡图。 要绘制一组坐标，请将 x 和 y 指定为等长向量。 要在同一组坐标区上绘制多组坐标，请将 x 或 y 中的至少一个指定为矩阵。

 fprintf - 将数据写入文本文件
    此 MATLAB 函数 按列顺序将 formatSpec 应用于数组 A1,...An 的所有元素，并将数据写入到一个文本文件。fprintf 使用在对 fopen 的调用中指定的编码方案。

fprintf(fileID,formatSpec,A1,...,An)
fprintf(formatSpec,A1,...,An)

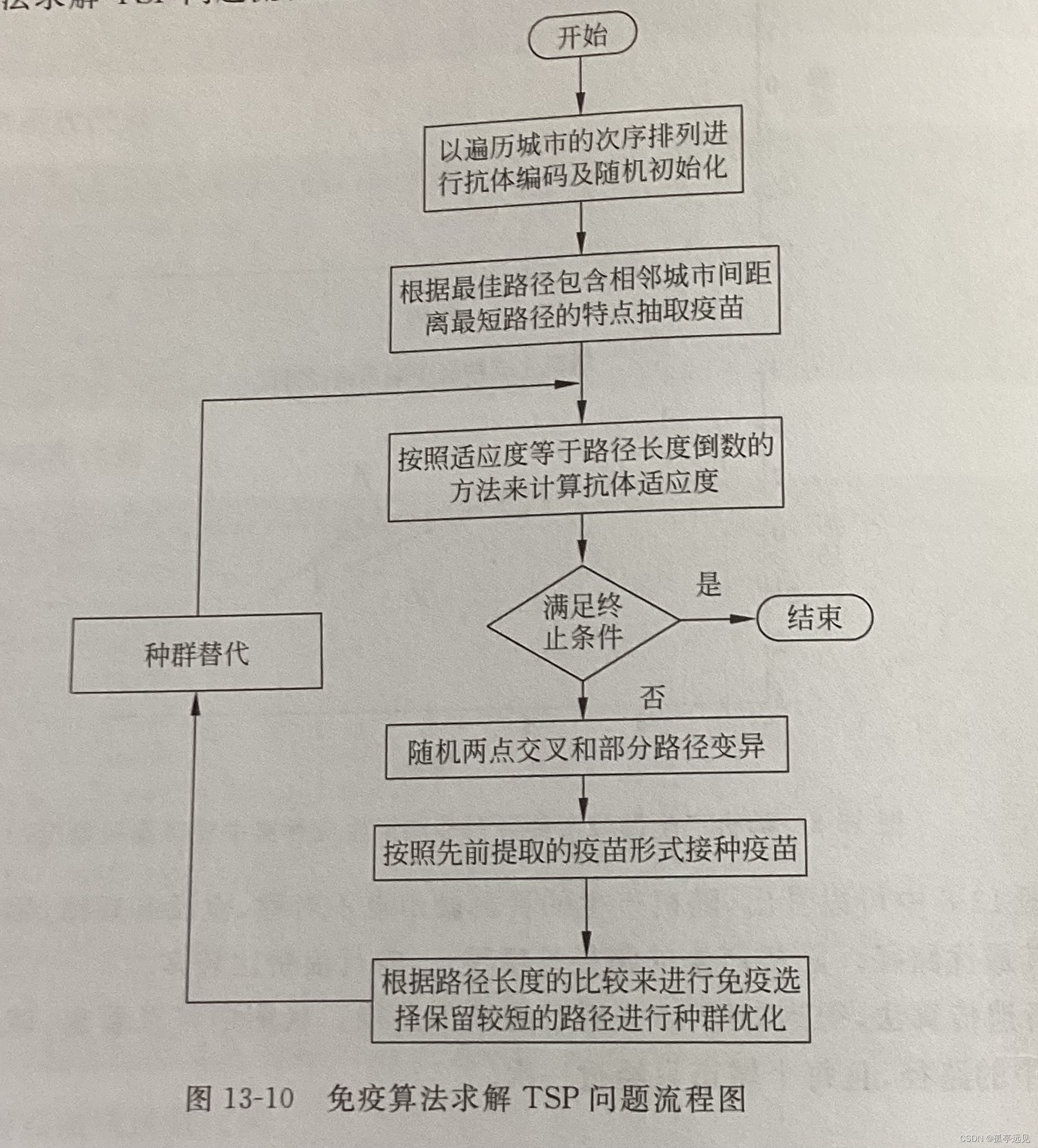
免疫算法

 基本流程

目标免疫 

        采用单点交叉和目标免疫。

 global - 将变量声明为全局变量    global var1 ... varN

%清空命令窗口和内存
clear
clc 
N=10;               
%城市的个数
M=N-1;               
%种群的个数
pos=randn(N,2);
%%生成城市的坐标
global D;
%城市距离数据
D=zeros(N,N);
for i=1:N
    for j=i+1:N
        dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2;
        D(i,j)=dis^(0.5);
        D(j,i)=D(i,j);
    end
end

%中间结果保存
global TmpResult;
TmpResult = [];
global TmpResult1;
TmpResult1 = [];

%参数设定
[M, N] = size(D);%集群规模
pCharChange = 1;%字符换位概率
pStrChange = 0.4;%字符串移位概率
pStrReverse = 0.4;%字符串逆转概率
pCharReCompose = 0.4;%字符重组概率
MaxIterateNum = 100;%最大迭代次数

%数据初始化
mPopulation = zeros(N-1,N);
mRandM = randperm(N-1);%最优路径
mRandM = mRandM + 1;
for rol = 1:N-1
    mPopulation(rol,:) = randperm(N);%产生初始抗体
    mPopulation(rol,:) = DisplaceInit(mPopulation(rol,:));%预处理
end

%迭代
count = 0;
figure(2);
while count < MaxIterateNum
    %产生新抗体
    B = Mutation(mPopulation, [pCharChange pStrChange pStrReverse pCharReCompose]);
    %计算所有抗体的亲和力和所有抗体和最优抗体的排斥力
    mPopulation = SelectAntigen(mPopulation,B);
    hold on
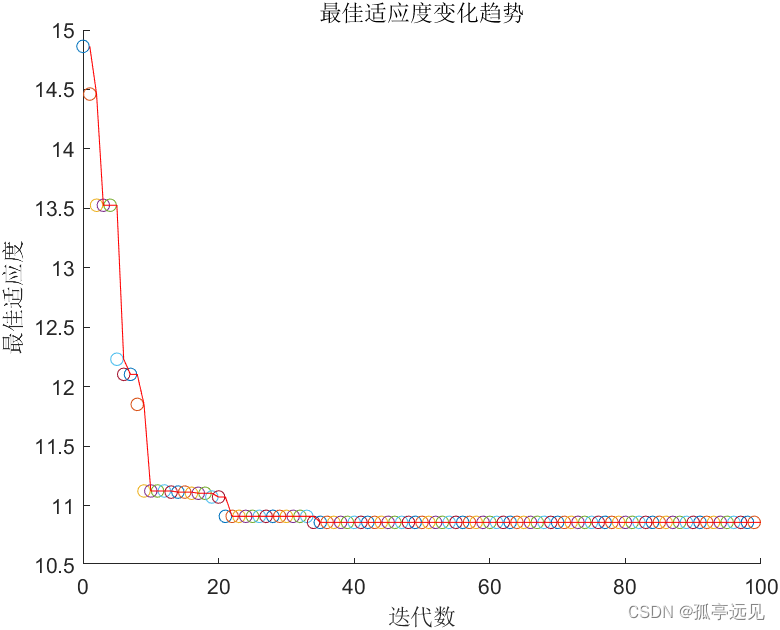
    plot(count,TmpResult(end),'o');
    drawnow
display(TmpResult(end));
display(TmpResult1(end));
    count = count + 1;
end

hold on
plot(TmpResult,'-r');
title('最佳适应度变化趋势')
xlabel('迭代数')
ylabel('最佳适应度')
% mRandM

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/592575.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL部署PXC集群-全网最详细

MySQL部署PXC集群-全网最详细

MySQL部署PXC集群 一&#xff0c;PXC了解 1.PXC介绍 Percona XtraDB Cluster&#xff08;简称PXC&#xff09; 是基于Galera的MySQL高可用集群解决方案 Galera Cluster是Codership公司开发的一套免费开源的高可用方案 PXC集群主要由两部分组成&#xff1a;Percona Server …
阅读更多...
计算机网络开荒1-概述

计算机网络开荒1-概述

文章目录 一、网络基本概述1.2 InternetInternet组成Internet服务角度 1.3 网络协议 二、计算机网络结构2.1 计算机网络结构2.1.1 网络边缘2.1.2 接入网络 物理介质2.1.2.1 DSL2.1.2.2 电缆网络2.1.2.3 家庭网络接入2.1.2.4 企业网络接入2.1.2.5 无线网络接入 2.1.3 网络核心 三…
阅读更多...
肉豆蔻酰六肽-4 /myristoyl hexapeptide-4, sympeptide230

肉豆蔻酰六肽-4 /myristoyl hexapeptide-4, sympeptide230

简介----肉豆蔻酰六肽-4 肉豆蔻酰六肽-4为胜肽系列应用最早和最广泛的多胜肽&#xff0c;国内外知名品牌普遍采用作为抗皱配方重要成分&#xff0c;在很多抗皱护肤产品中经常出现它的身影。它可以穿透真皮增加胶原蛋白&#xff0c;通过从内至外的重建来逆转皮肤老化的过程&…
阅读更多...
感应雷电浪涌的防线，SPD浪涌保护器

感应雷电浪涌的防线，SPD浪涌保护器

SPD - Surge Protective Device SPD 是防止雷击导致故障的避雷器&#xff0c;代表浪涌保护设备。一般指浪涌保护器&#xff0c;浪涌保护器&#xff0c;也叫防雷器&#xff0c;是一种为各种电子设备、仪器仪表、通讯线路提供安全防护的电子装置。 IEC/ EN61643-11 &#xff08…
阅读更多...
Vulkan Tutorial 8 深度缓冲

Vulkan Tutorial 8 深度缓冲

目录 26 三维几何图形 深度图像和视图 27 显式转换深度图像 渲染通道 帧缓冲区 清除值 深度和模版状态 处理窗口调整大小 26 三维几何图形 到目前为止&#xff0c;我们所处理的几何体是投射到三维的&#xff0c;但它仍然是完全平面的。在这一章中&#xff0c;我们要给位…
阅读更多...
（学习日记）2023.4.22

（学习日记）2023.4.22

写在前面&#xff1a; 由于时间的不足与学习的碎片化&#xff0c;写博客变得有些奢侈。 但是对于记录学习&#xff08;忘了以后能快速复习&#xff09;的渴望一天天变得强烈。 既然如此 不如以天为单位&#xff0c;以时间为顺序&#xff0c;仅仅将博客当做一个知识学习的目录&a…
阅读更多...
【C++】关键字：static

【C++】关键字：static

关键字static 在这一章节&#xff0c;将对C中的关键字static做进一步介绍。 成员函数中的this指针 这里先附上之前写的一个complex类代码&#xff1a; //防卫式定义 #ifndef __MYCOMPLEX__ #define __MYCOMPLEX__//前置声明 class complex;//类声明 complex& __doapl (…
阅读更多...
分享一个隐藏链接的样式

分享一个隐藏链接的样式

先上效果图&#xff1a; 再看代码&#xff1a; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>隐藏的链接按钮</title><style>.trapdoor {-webkit-transform: translateZ(0px);-webkit…
阅读更多...
Unity Addressables热更流程

Unity Addressables热更流程

一、分组&#xff08;网上教程一大堆&#xff09; 二、构建 构建前设置&#xff1a; 1、分组设置。所有组做远端构建加载选择&#xff0c;RemoteBuildPath 。RemoteLoadPath 2、AddressableAssetSettings设置 3、构建 三、导出信息分析&#xff1a; 1、Assets同级目录下&#…
阅读更多...
第十二届蓝桥杯国赛JavaB组题解

第十二届蓝桥杯国赛JavaB组题解

A. 整数范围 思路&#xff1a; 签到题。答案&#xff1a; 255 255 255 B. 纯质数 思路&#xff1a; 先用筛法筛出所有的质数&#xff0c;再根据题意判断&#xff0c;模板参考AcWing 数学知识。 代码&#xff1a; import java.io.BufferedReader; import java.io.IOExcepti…
阅读更多...
Python相关环境变量配置和模拟手机app登录

Python相关环境变量配置和模拟手机app登录

【java环境变量配置】 接着&#xff0c;打开系统->高级系统设置->环境变量。新建一个JAVA_HOME C:\Program Files\Java\jdk1.8.0_201&#xff08;这里是你的安装路径&#xff0c;最好复制粘贴&#xff09; 然后在Path下添加 %JAVA_HOME%\bin;%JAVA_HOME%\jre\bin; 然后…
阅读更多...
【LeetCode每日一题】——1493.删掉一个元素以后全为 1 的最长子数组

【LeetCode每日一题】——1493.删掉一个元素以后全为 1 的最长子数组

文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 滑动窗口 二【题目难度】 中等 三【题目编号】 1493.删掉一个元素以后全为 1 的最长子数组 …
阅读更多...
wx.request net::ERR_TOO_MANY_REDIRECTS

wx.request net::ERR_TOO_MANY_REDIRECTS

文章目录 问题解决方法一&#xff1a;请求头里添加Cookies方法二&#xff1a;使用weapp-cookie 问题 使用微信小程序开发者工具开发小程序项目时&#xff0c;wx.request 返回总是报 net::ERR_TOO_MANY_REDIRECTS wx.request发起一个get请求&#xff0c;一直重定向直到请求失败…
阅读更多...
Java Web——Session实现购物车

Java Web——Session实现购物车

实验名称&#xff1a; Session实现购物车 实验目的&#xff1a; &#xff08;1&#xff09;掌握什么是Cookie对象&#xff0c;掌握Cookie对象的使用 &#xff08;2&#xff09;掌握什么是Session对象&#xff0c;掌握Session对象的使用 &#xff08;3&#xff09;掌握使用…
阅读更多...
弗雷歇distanceDTW(动态时间规整)算法（附部分代码）

弗雷歇distanceDTW(动态时间规整)算法（附部分代码）

1、理论知识 1.1 什么是弗雷歇距离&#xff0c;它是用来干什么的&#xff1f; 费雷歇distance是求两个序列匹配之后的最大距离&#xff0c;这里需要明确a&#xff09;两个序列&#xff1b;b&#xff09;匹配过程&#xff1b;c&#xff09;最大距离的含义。 a&#xff09;两个…
阅读更多...
【java】 【Springboot】 开发通用审核流程服务模块

【java】 【Springboot】 开发通用审核流程服务模块

完全自研一个极其轻量级 通用审核流程服务 可以进行流程&#xff0c;节点配置&#xff0c;流程&#xff0c;节点审核人权限配置 批量审核&#xff0c;批量驳回&#xff0c;审核&#xff0c;驳回&#xff0c;批量退回第一步&#xff0c;退回第一步等操作 涉及数据库表单字段
阅读更多...
OSPF最优路径选择

OSPF最优路径选择

路由比较 1、内部区域＞区域间路由＞NSSA1＞Nssa2 2、如果只有Ex1、Ex2或者Nssa1、nNssa2开销类型。则Ex1＞Ex2或者Nssa1＞Nssa2 3、如果Ex1、Nssa1，Ex2和Nssa2，Ex1和Nssa1优于Ex2和Nssa2 4、如果外部开销加上内部开销，Ex1和Nssa1一样，则Ex1和Nssa1相同负载分担 5、如果外…
阅读更多...
CVE-2016-1000027安全漏洞分析和解决方案

CVE-2016-1000027安全漏洞分析和解决方案

文章目录 前言复现问题漏洞分析解决办法相关阅读 前言 CVE-2016-1000027 安全漏洞&#xff0c;该漏洞在5.x的最新版本(5.3.27)依然存在,官方未给出任何解决办法。在spring-web6.0之后&#xff0c;则不存在该漏洞。 受影响范围:spring-web<6.0 解决办法&#xff1a;升级到sp…
阅读更多...
【机器学习】分类问题和Logistic回归算法详解

【机器学习】分类问题和Logistic回归算法详解

在阅读本文前&#xff0c;请确保你已经掌握代价函数、假设函数等常用机器学习术语&#xff0c;最好已经学习线性回归算法&#xff0c;前情提要可参考https://blog.csdn.net/weixin_45434953/article/details/130593910 分类问题是十分广泛的一个问题&#xff0c;其代表问题是&…
阅读更多...
图表控件LightningChart JS v.4.1已经发布！引入虚线模式

图表控件LightningChart JS v.4.1已经发布！引入虚线模式

LightningChart JS是性能最高的JavaScript图表库&#xff0c;专注于实时数据可视化。是Web上性能最高的图表库具有出色的执行性能 - 使用高数据速率同时监控数十个数据源。 GPU加速和WebGL渲染确保您的设备的图形处理器得到有效利用&#xff0c;从而实现高刷新率和流畅的动画。…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023