来自编译原理课本,课本上讲的非常好,这里用我自己的方法再讲述一下。
讨论范围:2型文法,产生式的左边只有一个非终结符号。(这样才能构建树)
用语法树去进行巨型分析的时候会遇到的问题:
多个候选式的时候使用哪个候选式作为子节点?
假设我们提前知道使用某个候选式之后推导出的句型的首终结符是a,每个候选式推导出来的句型的首终结符是不一样的,这样我们就可以根据目标句型选择候选式了。
例如:
S→Ap|Bq
A→a|cA
B→b|dB
分析输入串W=ccap是否为文法的句子,则语法树如下图
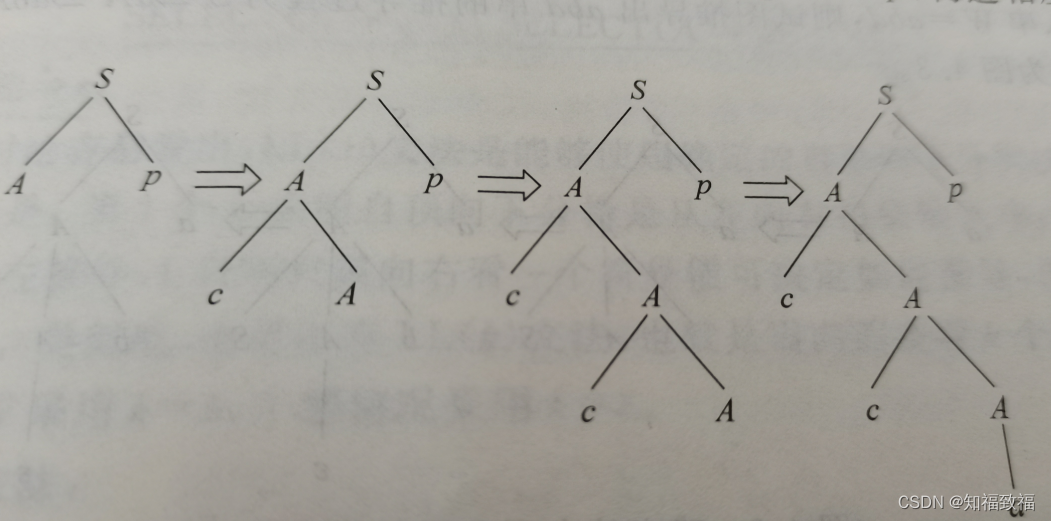
其中我们第一步为什么选择Ap而非Bq呢,因为只有A才能推导出c打头的字符串啊!选择B是没可能推导出来的。
这里就引出了第一个集合:first集合(首终结符集合)

但是有一种特殊情况是需要我们讨论的,如果存在候选式为ε的情况怎么办呢?怎么来确定我要不要选这个候选式呢?向后看一个,看看后面的终结符号。当你无法做选择的时候,不妨往后走一步,说不定你就知道怎么办了。
文法:
S→aA|d
A→bAS|ε
输出串W=abd

到第三步的时候我们选择A→ε是因为后面的S→d,引出follow集合(后面跟着的终结符集合)。

那么影响候选式选取的就有两个因素,既有first集,又有follow集合,归并一下,那就是select集合。

不能推导出空的时候只看first,能推导出空的时候就需要考虑follow集合啦。
LL(1)文法的判别也就出来啦:同一非终结符号的候选式的select集合没有交集(这样才能选择)。
求first集的步骤
- A的候选式以终结符号a开头的,把a加入到first(A)
- A的候选式以非终结符B开头的,把first(B)加入first(A)
- 注意如果有A→BC···,B→ε,first(C)包含于first(A)
一些注意事项:
第二步和第三步最好写出所有的包含关系再添加,因为很可能前期刚把first(B)加入first(A),后期B又被扩充了,这样就需要再次添加,直到各个集合不再扩大。也就是说这个包含关系是适用于最终结果的。
求follow集的步骤
- 看产生式的右边,如果出现···Aa···,把a加到follow(A)里面
- 如果出现···AB···,把first(B)- ε 加到follow(A)里面
- 如果出现B→···A,follow(B)包含于follow(A)
- 讨厌的空规则又来了,如果有B→···AC,C→ε,
follow(B)包含于 follow(A)
注意事项和first集差不多,就是空规则和包含关系。还有follow集里面没有ε哦,以及加入一个 # .
select集,略
LL(1)分析表,面向select集填产生式的右边
表驱动的LL(1)分析
三列:步骤、分析栈、符号串
注意分析栈是个栈,需要逆序进栈!!