DFS专题

news2024/11/27 15:42:10

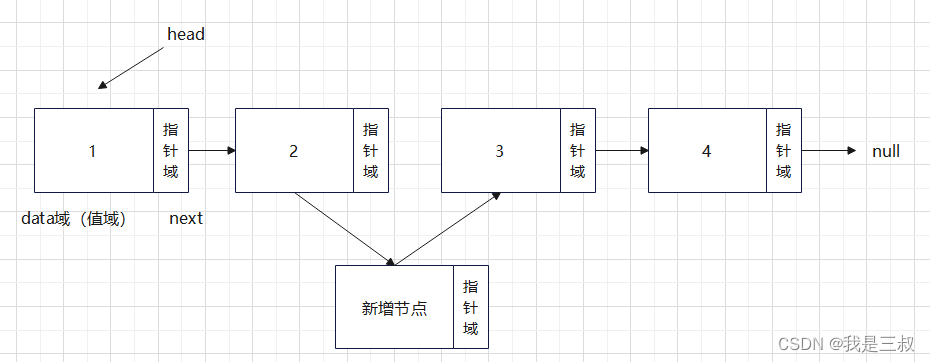
题单地址：【237题】算法基础精选题单_ACM竞赛_ACM/CSP/ICPC/CCPC/比赛经验/题解/资讯_牛客竞赛OJ_牛客网

老子的全排列呢

dfs+回溯

int n = 8;
int idx;
int record[10];
bool vis[10];

void dfs(int num)
{
	if(num==n){
		for(int i=1;i<=n;i++) cout<<record[i]<<" ";
		cout<<endl;
		return ;
	}
	for(int i=1;i<=n;i++){
		if(!vis[i]){
			vis[i] = true;
			record[++idx] = i;
			dfs(num+1);
			record[idx--] = 0;
			vis[i] = false;
		}
	}

}

N皇后问题

O(n!)

 借用一位博主的图说明x+y和x-y+n的

const int N = 15*2;
int n,ans;
int col[N],dig[N],undig[N];

void dfs(int u)//u代表行数
{
	if(u == n){//已经搜索了n行
		ans++;
		return ;
	}
	for(int y=0;y<n;y++){
		if(!col[y] && !dig[u+y] && !undig[u-y+n]){
			col[y] = dig[u+y]  = undig[u-y+n] = true;
			dfs(u+1);
			col[y] = dig[u+y]  = undig[u-y+n] = false;
		}
	}
}

void solve()
{
	cin>>n;
	dfs(0);
	cout<<ans<<endl;
}

O(2^(n*n))

TLE的写法,想想就可怕

const int N = 15*2;
int n,ans;
int col[N],row[N],dig[N],undig[N];

void dfs(int x,int y,int u)
{
	if(y==n){
		x++;
		y=0;
	}
	if(x==n){
		if(u==n) ans++;
		return;
	}

	//不放
	dfs(x,y+1,u);
	//放
	if(!col[y]&&!row[x]&&!dig[x-y+n]&&!undig[x+y]){
		col[y] = row[x] = dig[x-y+n] = undig[x+y] = true;
		dfs(x,y+1,u+1);
		col[y] = row[x] = dig[x-y+n] = undig[x+y] = false;
	}

}

void solve()
{
	cin>>n;
	dfs(0,0,0);
	cout<<ans<<endl;
}

马踏棋盘

走迷宫的写法，和迷宫的上下左右稍有不同，深搜时注意别越界且前往的点上没走过即可

#define PII pair<int,int>
const int N = 15+2;
int n,m;
const PII dir[4] = {{1,2},{2,1},{-1,2},{-2,1}};
bool vis[N][N];
int ans;

bool in(int x,int y)
{
	return (x>=1 && x<=n && y>=1 && y<=m);
}

void dfs(int x,int y)
{
	if(x==n && y==m){
		ans++;
		return;
	}

	for(int i=0;i<4;i++){
		int tx = dir[i].first+x;
		int ty = dir[i].second+y;
		if(in(tx,ty) && !vis[tx][ty]){
			vis[tx][ty] = true;
			dfs(tx,ty);
			vis[tx][ty] = false;
		}
	}
}

void solve()
{
	cin>>n>>m;
	vis[1][1] = true;
	dfs(1,1);
	cout<<ans<<endl;
}

数独挑战

dfs+剪枝，棋盘格子看起来很多觉得会TLE，实际上考虑上数独的规则进行剪枝还是可以过的。

分为三部分记录棋盘信息：行、列、块，块分为

 11 |  12 | 13

 21 |  22 | 23

 31 |  32 | 33

一共九个部分，(x,y)在某一块可以用[x/3][y/3]来确定位置

其余的部分和常规dfs相差无几，注意的是回溯的时候不能都置为0，只有你自己填的数可以删掉，题目原来给的数不能删，所以要额外开一个origin数组记录哪些位置是一开始就有数的

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fasten cin.tie(0),cout.tie(0);ios::sync_with_stdio(false)

const int N = 10+2;
int g[N][N];
bool row[N][10];//第i行的1-9各有几个
bool col[N][10];
bool block[4][4][10];//左上角的块为1,1 依次为1,2 1,3 ... 
int blank = 81;//待填的空格
int origin[N][N];//记录原始给定的数字，回溯时不能删除
void print(){
    for(int i=0;i<9;i++){
        for(int j=0;j<9;j++){
            cout<<g[i][j]<<" ";
        }
        cout<<endl;
    }
}
void dfs(int x,int y)
{
    if(y==9){
        y = 0;
        x++; 
    }
    if(blank==0){
        print();
        return ;
    }
    if(g[x][y]!=0) dfs(x,y+1);
    bool flag = false;//记录该格子是否还能填数，不能的话该搜索路径不用搜索下去了
    for(int i=1;i<=9;i++){
        if(!block[x/3][y/3][i] && !row[x][i] && !col[y][i]){
            flag = true;
            g[x][y] = i;
            block[x/3][y/3][i] = row[x][i] = col[y][i] = true;
            blank--;
            dfs(x,y+1);
            blank++;
            //若是自己填的数就回溯为0，系统给定的数不能改动
            if(origin[x][y]) g[x][y] =origin[x][y];
            else g[x][y] = 0;
            block[x/3][y/3][i] = row[x][i] = col[y][i] = false;
        }
    }
    if(!flag) return ;

}
void solve()
{
    for(int i=0;i<9;i++){
        for(int j=0;j<9;j++){
            cin>>g[i][j];
            origin[i][j] = g[i][j];
            if(g[i][j]!=0){
                int e = g[i][j];
                blank--;
                row[i][e] = true;
                col[j][e] = true;
                block[i/3][j/3][e] = true;
            }
        }
    }
    //debug
    // for(int i=1;i<=9;i++) cout<<i<<" ";
    // cout<<endl;
    // for(int i=0;i<3;i++){
    //     for(int k=0;k<3;k++){
    //         for(int j=1;j<=9;j++){
    //             cout<<block[i][k][j]<<" ";
    //         }
    //         cout<<endl;
    //     }
    // }
    dfs(0,0);

}
signed main()
{
    fasten;
//     freopen("stdin.txt","r",stdin);
//     freopen("stdout.txt","w",stdout);
    solve();
    return 0;
}

幸运数字Ⅱ

可以先用dfs把所有只含4or7且<=1e9的数处理出来放在一个容器内，然后再[l,r]内使用二分计算总和，用string比用long long快大约100倍左右

#define PII pair<int,int>
#define ll long long
vector<ll>v;

void dfs(string s,int digit)
{
	if(digit>9){
		return ;
	}
	int tmp = 0;
	for(int i=0;i<s.length();i++){
		tmp = tmp*10+(s[i]-'0');
	}
	if(tmp<1e9){
		if(tmp!=0) v.push_back(tmp);
		dfs("4"+s,digit+1);
		dfs("7"+s,digit+1);
	}
}

void solve()
{
	dfs("",0);
	v.push_back(4444444444);
	sort(v.begin(),v.end());
	// for(auto it:v){
	// 	cout<<it<<endl;
	// }
	long long l,r;
	cin>>l>>r;
	long long res = 0;
	for(ll i=l;i<=r;){
		auto it = lower_bound(v.begin(),v.end(),i);
		res += min(r-i+1ll,(*it-i+1ll))*(*it);
		i = *it+1;
	}
	cout<<res<<endl;
}

[NOIP2017]奶酪

回溯dfs写法会超时，别写回溯写法

有的题目一定要回溯，但是有的题目不用回溯，选择不回溯可以优化算法

那什么时候不需要回溯？

当遇到一个选择时，一定要对它操作时，那么就不需要回溯。比如要标记求所有情况，找到了就要标记。如果取消标记，那么就会重复计算。在这道题中，小鼠尝试通过空洞从起点到终点，到达一个点时，小鼠需要知道该点范围内的可到达的点中有没有能到达终点的点，如果有的点不能到达终点，就不必再走那个点了。

如何知道该点能不能达到终点？

dfs搜索时会直接搜索到最深处，接着从底层一层一层往上反馈该点能不能通往终点。该点若已经搜索过，必定打上了标记（回溯则会把该标记划去，那就需要重复搜索了）

AC版本

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define int long long
#define fasten cin.tie(0),cout.tie(0);ios::sync_with_stdio(false)


const int N = 1000+2;
int n;
int h,r;
bool vis[N];//记录该空洞有没有走过
bool g[N][N];
int x[N],y[N],z[N];
bool isfind = false;

bool dfs(int i)
{
    if(z[i]+r>=h){
        return true;
    }
    if(vis[i]) return false;
    vis[i] = true;
    for(int j=0;j<n;j++){
        if(g[i][j] && dfs(j)) return true;
    }
    return false;
}

void solve()
{
    int t;
    cin>>t;
    while(t--){
        memset(g,0,sizeof g);
        memset(vis,0,sizeof vis);
        cin>>n>>h>>r;
        for(int i=0;i<n;i++){
            cin>>x[i]>>y[i]>>z[i];
        }

        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                if(i!=j)g[i][j]=g[j][i]=(x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])+
                                  (z[i]-z[j])*(z[i]-z[j]) <=4*r*r;
            }
        }
        for(int i=0;i<n;i++){
            if(z[i]<=r){
                if(dfs(i)){
                    puts("Yes");
                    isfind = true;
                    break;
                }
            }
        }
        if(!isfind) puts("No");
        isfind = false;
    }
}
signed main()
{
    fasten;
//     freopen("stdin.txt","r",stdin);
//     freopen("stdout.txt","w",stdout);
    solve();

    return 0;
}

TLE版本

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fasten cin.tie(0),cout.tie(0);ios::sync_with_stdio(false)

class point
{
public:
    double x,y,z;
    point(){};
    point(int a,int b,int c){x=a,y=b,z=c;}
};

double dist(point p1,point p2)
{
    double x = (p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)+(p1.z-p2.z)*(p1.z-p2.z);
    return sqrt(x);
}
const int N = 1000+2;
point a[N];
int n;
double h,r;
bool vis[N];//记录该空洞有没有走过
bool g[N][N];
bool isfind = false;

void dfs(int x,int y,int z,int idx)
{
    if(z+r>=h){
        isfind = true;
        return ;
    }
    for(int i=0;i<n;i++){
        point tmp(x,y,z);
        if(!vis[i] && g[idx][i]){
            vis[i] = true;
            dfs(a[i].x,a[i].y,a[i].z,i);
            vis[i] = false;
        }
    }

}
void solve()
{
    int t;
    cin>>t;
    while(t--){
        memset(g,0,sizeof g);
        cin>>n>>h>>r;
        for(int i=0;i<n;i++){
            cin>>a[i].x>>a[i].y>>a[i].z;
        }

        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                if(i!=j)g[i][j] = dist(a[i],a[j])<=2*r;
            }
        }
        for(int i=0;i<n;i++){
            if(a[i].z<=r) dfs(a[i].x,a[i].y,a[i].z,i);
        }
        if(isfind) puts("Yes");
        else puts("No");
        isfind = false;
    }
}
signed main()
{
    fasten;
//     freopen("stdin.txt","r",stdin);
//     freopen("stdout.txt","w",stdout);
    solve();

    return 0;
}

wyh的迷宫

迷宫问题不在赘述

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define int long long
#define fasten cin.tie(0),cout.tie(0);ios::sync_with_stdio(false)
#define PII pair<int,int>
const int N = 500+2;
int n,m;
const PII dir[4] = {{0,1},{1,0},{-1,0},{0,-1}};
bool vis[N][N];
string s[N];
PII _begin,_end;
bool isfind = false;

bool in(int x,int y)
{
	return (x>=1 && x<=n && y>=1 && y<=m);
}

void dfs(int x,int y)
{
    //cout<<x<<" "<<y<<endl;
    if(x==_end.first && y==_end.second){
        isfind = true;
        return ;
    }
	for(int i=0;i<4;i++){
		int tx = dir[i].first+x;
		int ty = dir[i].second+y;
		if(in(tx,ty) && !vis[tx][ty] && s[tx][ty]!='x'){
            if(x==_end.first && y==_end.second){
                isfind = true;
                return ;
            }
			vis[tx][ty] = true;
			dfs(tx,ty);
		}
	}
    return ;
}

void solve()
{
    int t;
    cin>>t;
    while(t--){
        memset(vis,0,sizeof vis);
        cin>>n>>m;
        for(int i=1;i<=n;i++) cin>>s[i],s[i]=" "+s[i];
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                if(s[i][j]=='s') _begin = {i,j};
                else if(s[i][j]=='t') _end = {i,j};
            }
        }
        vis[_begin.first][_begin.second] = true;
        dfs(_begin.first,_begin.second);
        if(isfind) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
        isfind = false;
    }
}


signed main()
{
    fasten;
//     freopen("stdin.txt","r",stdin);
//     freopen("stdout.txt","w",stdout);
    solve();
    return 0;
}

Lake Counting

求连通分支的个数，可用并查集的知识

也可以直接搜索，标记访问过的点，查看有几块

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define int long long
#define fasten cin.tie(0),cout.tie(0);ios::sync_with_stdio(false)
#define PII pair<int,int>
const int N = 100+5;
char s[N][N];
int n,m;
int ans;
const PII dir[8] = {{1,0},{1,1},{1,-1},{0,1},
                    {0,-1},{-1,1},{-1,0},{-1,-1}};

bool in(int x,int y)
{
    return (x>=0 && x<n && y>=0 && y<m);
}

void dfs(int x,int y)
{
    s[x][y] = '.';//走过的修改成陆地
    for(int i=0;i<8;i++){//八个方向都可走
        int tx = x+dir[i].first;
        int ty = y+dir[i].second;
        if(in(tx,ty) && s[tx][ty]=='W'){
            dfs(tx,ty);
        }
    }
    return ;
}
void solve()
{
    cin>>n>>m;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            cin>>s[i][j];
        }
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(s[i][j]=='W'){
                dfs(i,j);
                ans++;
            }
            
        }
    }
    cout<<ans<<endl;
}


signed main()
{
    fasten;
//     freopen("stdin.txt","r",stdin);
//     freopen("stdout.txt","w",stdout);
    solve();
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/590797.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【ONE·C++ || C++11（一）】

【ONE·C++ || C++11（一）】

总言 主要介绍C11中的一些功能语法。 文章目录 总言0、思维导图1、基本情况简介2、统一的列表初始化2.1、{}的使用2.2、initializer_list2.2.1、基础介绍2.2.2、在各容器中实现说明 3、声明3.1、auto3.2、nullptr3.3、decltype 4、范围for5、智能指针6、STL中一些变化6.1、C11…
阅读更多...
一、版本控制

一、版本控制

1、什么是版本控制 1.1、版本控制的概念 版本控制&#xff08;Revision control&#xff09;是一种在开发的过程中用于管理我们对文件、目录或工程等内容的修改历史&#xff0c;方便查看更改历史记录&#xff0c;备份以便恢复以前的版本的软件工程技术。 1.2、版本控制的作用…
阅读更多...
泛型方法、Function类的函数化编程与调用

泛型方法、Function类的函数化编程与调用

0、引言 在项目开发的过程中&#xff0c;常常需要将一些高频复用的方法封装成工具类&#xff0c;例如最近学到的Redis缓存中&#xff0c;解决缓存穿透、解决缓存击穿的方法&#xff08;例如解决缓存穿透的问题的方法queryWithPassThrough&#xff09;&#xff0c;传入一个Long型…
阅读更多...
谷粒商城：Oss endpoint can‘t be empty.问题

谷粒商城：Oss endpoint can‘t be empty.问题

商品API &#xff0c;文件上传管理的时候 出现这个问题 解决两个方向 1.springBoot、alibabaCloud、springCloud、aliyunOSS 之间的版本问题&#xff0c;我的是下面的版本可以运行了。 // springBoot版本 2.7.7 <groupId>org.springframework.boot</groupId> &l…
阅读更多...
中关村论坛 | 金融业从增量到存量博弈背后两大原因 更重要的是……

中关村论坛 | 金融业从增量到存量博弈背后两大原因 更重要的是……

在数字经济浪潮下&#xff0c;中国金融业正在经历数字化转型的深刻变革。为研判金融科技行业发展趋势和前景&#xff0c;探索金融创新与监管安全的边界&#xff0c;“2023中关村论坛金融科技论坛”于5月29日召开。 中电金信常务副总经理冯明刚与中国银行软件中心副总经理康钧伟…
阅读更多...
链表：虚拟头节点你会用吗？

链表：虚拟头节点你会用吗？

大家好&#xff0c;我是三叔&#xff0c;很高兴这期又和大家见面了&#xff0c;一个奋斗在互联网的打工人。 前言&#xff1a;什么是链表 什么是链表&#xff0c;链表是一种通过指针串联在一起的线性结构&#xff0c;每一个节点由两部分组成&#xff0c;一个是数据域一个是指…
阅读更多...
提高用户忠诚度的 4 种客户保留策略

提高用户忠诚度的 4 种客户保留策略

什么是客户保留&#xff1f;简而言之&#xff0c;客户保留是指企业用来鼓励现有客户群重复购买和持续忠诚度的策略和战术。根据最近的研究&#xff0c;多达68%的客户在觉得公司不重视他们的业务时会转向竞争对手。 这就是为什么客户保留对各行各业的企业都如此重要的原因。与获…
阅读更多...
《程序员面试金典（第6版）》面试题 16.25. LRU 缓存（自定义双向链表，list库函数，哈希映射）

《程序员面试金典（第6版）》面试题 16.25. LRU 缓存（自定义双向链表，list库函数，哈希映射）

题目描述 设计和构建一个“最近最少使用”缓存&#xff0c;该缓存会删除最近最少使用的项目。缓存应该从键映射到值(允许你插入和检索特定键对应的值)&#xff0c;并在初始化时指定最大容量。当缓存被填满时&#xff0c;它应该删除最近最少使用的项目。 题目传送门&#xff1a;…
阅读更多...
消息队列内容

消息队列内容

问题有哪些&#xff1f; &#xff08;1&#xff09;消息队列为什么会出现&#xff1f; &#xff08;2&#xff09;消息队列能用来干什么&#xff1f; &#xff08;3&#xff09;使用消息队列存在的问题&#xff1f; &#xff08;4&#xff09;如何解决重复消费的问题&#…
阅读更多...
PyCharm安装使用教程

PyCharm安装使用教程

简介 PyCharm是一种PythonIDE&#xff08;Integrated Development Environment&#xff0c;集成开发环境&#xff09;&#xff0c;带有一整套可以帮助用户在使用Python语言开发时提高其效率的工具&#xff0c;比如调试、语法高亮、项目管理、代码跳转、智能提示、自动完成、单…
阅读更多...
docker-安装redis集群

docker-安装redis集群

目录 1.服务器列表 2.安装docker 3.docker内网IP地址配置 4.docker安装redis集群 1.选择合适数据位置 2.循环生成redis配置目录 3.打开宿主机防火墙端口 4.循环生成redis容器 5.创建集群命令 6.命令行集群验证 1.服务器列表 服务器列表 nameip远程端口用户名/密码cen…
阅读更多...
One2Multi Graph Autoencoder for Multi-view Graph Clustering

One2Multi Graph Autoencoder for Multi-view Graph Clustering

One2Multi Graph Autoencoder for Multi-view Graph Clustering | Proceedings of The Web Conference 2020 (acm.org) 目录 Abstract 1 Introduction 2 Model 2.1 Overview 2.2 One2Multi Graph Convolutional Autoencoder Informative graph convolutional encoder M…
阅读更多...
Eclipse教程 Ⅸ

Eclipse教程 Ⅸ

今天继续来学习Eclipse 快速修复、Eclipse 浏览菜单、Eclipse 查找以及Eclipse 悬浮提示的内容&#xff01;老规矩&#xff0c;废话不多说&#xff0c;开始吧。 Eclipse 快速修复 使用快速修复 在 Eclipse 编辑器中当你输入字母时&#xff0c;编辑器会对你输入的内容进行错误…
阅读更多...
PostgreSQL FDW

PostgreSQL FDW

一、FDW简单理解 FDW (foreign-data wrapper&#xff0c;外部数据包装器)&#xff0c;PostgreSQL FDW 是一种外部访问接口&#xff0c;它可以被用来访问存储在外部的数据&#xff0c;这些数据可以是外部的pg数据库&#xff0c;也可以oracle、mysql等数据库&#xff0c;甚至可以…
阅读更多...
大气气溶胶期末复习笔记

大气气溶胶期末复习笔记

大气气溶胶期末复习笔记 大气气溶胶 广义&#xff1a;指悬浮在大气中的各种固态和液态微粒与大气构成的混合体系 狭义&#xff1a;指大气中悬浮的各种固态粒子&#xff0c;简称气溶胶粒子 来源 直接注入 通过地表直接注入大气固体&#xff0c;液体物质的破碎过程中产生&…
阅读更多...
筛质数—(埃氏筛欧拉筛)

筛质数—(埃氏筛欧拉筛)

埃氏筛&欧拉筛 埃氏筛欧拉筛 例题&#xff1a;AcWing 868. 筛质数 对欧拉筛的理解不是很深刻&#xff0c;写下自己的理解&#xff0c;加深一下理解&#xff0c;也方便后期忘记后再学习 埃氏筛 埃氏筛的主要思想是让质数x去筛掉x的所有合数&#xff0c;这个比较容易理解。…
阅读更多...
机器学习知识经验分享之五：R语言安装

机器学习知识经验分享之五：R语言安装

python语言用于深度学习较为广泛&#xff0c;R语言用于机器学习领域中的数据预测和数据处理算法较多&#xff0c;后续将更多分享机器学习数据预测相关知识的分享&#xff0c;有需要的朋友可持续关注&#xff0c;有疑问可以关注后私信留言。 目录 一、R语言介绍 二、R语言安装…
阅读更多...
装饰器模式：实现类功能的动态扩展

装饰器模式：实现类功能的动态扩展

一&#xff0c;简介 装饰器模式&#xff08;Decorator Pattern&#xff09;是一种结构型设计模式&#xff0c;它允许在不修改原有类结构的情况下&#xff0c;给一个对象动态添加额外的职责。通常情况下&#xff0c;扩展一个类的功能我们首先会想到用继承方式来实现&#xff0c…
阅读更多...
7步搞懂手写数字识别Mnist

7步搞懂手写数字识别Mnist

大家好啊&#xff0c;我是董董灿。 图像识别有很多入门项目&#xff0c;其中Mnist 手写数字识别绝对是最受欢迎的。 该项目以数据集小、神经网络简单、任务简单为优势&#xff0c;并且集合了CNN网络中该有的东西&#xff0c;可谓麻雀虽小&#xff0c;五脏俱全。 非常适合新手…
阅读更多...
Fourier分析入门——第12章——Fourier变换的性质

Fourier分析入门——第12章——Fourier变换的性质

目录 第12章 Fourier变换的性质 12.1 引言 12.2 Fourier变换性质的相关定理 12.2.1 线性定理(Linearity) 12.2.2 伸缩性定理(Scaling) 12.2.3 时间/空间平移定理(Shift) 12.2.4 频移定理 12.2.5 调制定理(Modulation) 12.2.6 微分定理(Differentiation) 12.2.7 积分定…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023