埃氏筛&欧拉筛
- 埃氏筛
- 欧拉筛
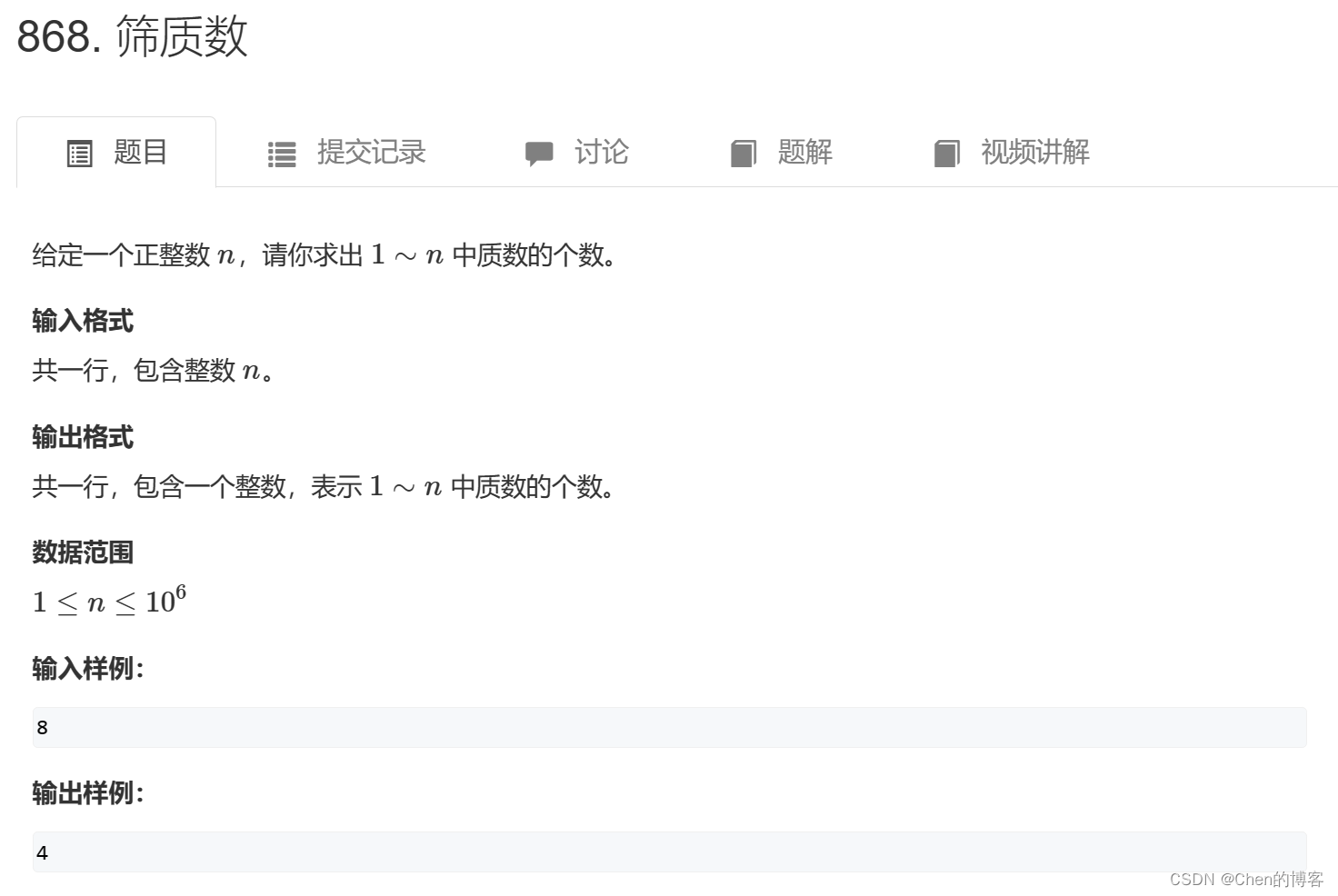
例题:AcWing 868. 筛质数
对欧拉筛的理解不是很深刻,写下自己的理解,加深一下理解,也方便后期忘记后再学习
埃氏筛
埃氏筛的主要思想是让质数x去筛掉x的所有合数,这个比较容易理解。
合数都是由质数构成,所以合数一定会被其合数筛掉。
举个例子:
质数2,可以筛掉合数4,6,8,...2k (2k<=n)
质数3,可以筛掉合数6,9,12,....,3k (3k<=n)
质数5,可以筛掉合数5,10,15,....,5k (5k<=n)
有这个思想就能得到
O
(
n
l
o
g
l
o
g
n
)
O(nloglogn)
O(nloglogn)的算法埃氏筛
代码如下:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e6+10;
int f[N],idx=0;
bool st[N];
int main(){
int n;
cin>>n;
st[1]=1;
for(int i=2;i<=n;i++)
if(!st[i]){
f[idx++]=i;
st[i]=1;
for(int j=i;j<=n;j+=i) st[j]=1;
}
cout<<idx;
return 0;
}
欧拉筛
欧拉筛也叫做线性筛,时间复杂度是
O
(
n
)
O(n)
O(n)的
观察埃氏筛的筛合数过程,我们可以发现,一个合数有可能被多个质数筛掉
比如,合数30,会被质数2,3,5都筛一次,这就导致了埃氏筛不是线性的,那么如何改变才能让每个合数只会被筛掉一次呢?
我们考虑一个合数y,让y最小的合数来筛掉y,例如上面的例子,只让30被2筛掉
代码如下:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e6+10;
int f[N],idx=0;
bool st[N];
int main(){
int n;
cin>>n;
for(int i=2;i<=n;i++){
if(!st[i]) f[idx++]=i;
for(int j=0;f[j]<=n/i;j++){
st[f[j]*i]=true;
if(i%f[j]==0) break;
}
}
cout<<idx;
return 0;
}
我们分析这段代码为什么能做到每个合数都会被筛掉,并且每个合数都会被其最小的质数筛掉。
数组f[]用来存i及其之前的质数
st[f[j]*i]=true;表示用质数f[j]筛掉合数f[j]*i
if(i%f[j]==0) break;来保证合数f[j]*i只会被其最小质数筛掉
解释一下原因:
i%f[j]==0说明f[j]是i的最小质数(如果不是,在进行到f[j]之前就break掉了),
i为合数,如果不break掉,那么f[j+1]*i会被f[j+1]筛掉,
但是i的最小质数是f[j],f[j+1]>f[j],f[j+1]*i的最小质数是f[j],所以要break掉,等待下一个合数i=(f[j+1]*i)/f[j]时,f[j]就能消掉f[j+1]*i。
为什么合数一定会被消掉?
合数y可以分解成=y的最小质数x*(y/x),按照算法的流程,当i==(y/x)时,y一定会被x消掉
为什么循环里要写f[j]<=n/i?
这个相当于f[j]*i<=n,当f[j]*i>n时,消掉的数>n,超过了我们需要的范围,无意义
为什么能保证j<idx,也就是说质数数组f里的质数用完之前一定会break掉,结束循环
这个是由i来决定的,
如果i为质数:那么在进入第二层循环之前i就被添加到数组f中了,
也就是说i为质数的话,会在最后一次被自己筛掉。
如果i为合数:那么i一定会在自己最小的质数x处break掉,
所以质数数组f里的质数用完之前一定会break掉