大气气溶胶期末复习笔记

大气气溶胶

广义：指悬浮在大气中的各种固态和液态微粒与大气构成的混合体系
狭义：指大气中悬浮的各种固态粒子，简称气溶胶粒子

来源

直接注入

• 通过地表直接注入大气
• 固体，液体物质的破碎过程中产生，注入大气
• 高空注入
• 比如：火山喷发，扬尘，花粉，海浪泡沫破碎，飞机直接排放，陨石等

二次生成

新粒子生成事件的判断

• 颗粒物的数谱分布出现一个新的模态
• 新的模态在大气中存在一段时间
• 同时新模态呈现增长趋势

气相粒子核化过程

物理过程

• 同质核化
• 异质核化

化学过程

• 通过化学反应产生新的固相粒子
• 气体分子被固体粒子表面的化学键作用吸附在粒子表面

气溶胶尺度分类

• 超细粒子：
  • 核模态：1-10nm
  • 爱根模态：10-100nm
• 细粒子：
  • 积聚模态：100-1000nm
• 粗粒子：
  • 大于1微米

各个尺度粒子的来源

• 核模态：气相粒子凝结，聚合增长
• 爱根核模态：燃烧产生的一次气溶胶粒子，气体分子通过化学反应转化成的二次气溶胶粒子
• 积聚模态：爱根核粒子的聚集，以及二次气溶胶，尤其是硫酸盐
• 粗模态：机械过程，直接排放，火山灰，生物质气溶胶

气溶胶尺寸特征（各种等效粒径）

动力学等效直径

在低雷诺数的静止空气中，与实际粒子具有相同沉降速度的单位密度球体的直径

斯托克斯等效直径

在低雷诺数的静止空气中，与实际粒子具有相同沉降速度的相同密度球体的直径

光学等效直径

与所研究的粒子具有相同的光散射能力的直径

浓度谱分布

• 数浓度：个数/体积
• 质量浓度：质量/体积
• 表面积浓度：表面积/体积
• 体积浓度：$\mu m^3/m^3$

计算

• 数浓度平均半径：$\bar{r}=\frac{1}{n}{\sum }_{i=1}^M{n}_i{r}_i，n表示总的粒子数目，求和的就是各个粒径半径对个数的加权$
• 众数半径：数浓度最大对应的半径
• 中值半径：小于中值半径与大于中值半径的粒子数相等

主要的化学组成

• 微量元素
• 有机物
• 离子成分：Na+,K+,Ca2+,NH4+,SO42-, NO3-

污染源解析

区分和识别大气污染的复杂来源，并对气溶胶中的污染物的来源进行定性或定量分析其贡献的技术

• 从排放源解析：
  • 源清单：对各种污染物的详细调查，确定各污染源对总排放的贡献
  • 扩散模式：根据污染物排放，迁移，扩散，化学转化等过程，估算污染源对气溶胶质量浓度的贡献
• 从受体解析：
  • 分析气溶胶成分和物理特性来推断污染物来源
  • 受体解析中化学法最为成熟

受体模式的几种常用源解析方法

相对浓度法

丰度：大气气溶胶中所研究元素浓度与总气溶胶浓度的比值

• 相对浓度稳定意味着污染源的变化不大
• 不能判断污染源类型，也不能判断不同污染源的贡献率

富集因子：判断气溶胶粒子中元素的富集成都，判断气溶胶粒子中元素的自然来源和人为来源，关键在于选定一种相对稳定的元素作为参比元素

化学质量平衡法

受体大气气溶胶的总质量浓度来自于n类源贡献的质量浓度，该方法基于大气中污染物的化学组成和受体点观测数据，通过解质量平衡方程来估算不同源类别的贡献程度

因子分析法

找出控制所有变量的少数公因子，将每个指标变量表示成公因子的线性组合，通过少数几个独立的因子尽可能多地反映出因子所反映的信息

• 假设污染物中第i个元素是由k个污染源贡献的线性组合

后向轨迹法

该方法基于大气流场数据和反演技术，通过模拟污染物从受体点倒退到其可能的起源地点，以追踪和识别污染物来源

气溶胶粒子的清除

干沉降

气溶胶在大气中的滞留时间指的是气溶胶颗粒在大气中停留的平均时间长度
气载物通过重力下降，扩散传输，或两者共同作用，沉积于地表面从而从大气移除或通过于表面碰撞或被突出物拦截而移出

发生原因

• 受重力影响
• 随气流输送的气溶胶粒子受障碍物拦截
• 小粒子与大粒子碰撞产生镇江
• 布朗运动产生的随机碰撞产生沉降
• 湍流输送中的碰撞
• 各种泳移过程中的碰撞

影响因素

• 大气输送特征
• 气溶胶粒子的物理化学特征
• 沉降表面和下垫面特征

干沉降速度

• 与气溶胶粒子受到的阻力（空气动力学阻力，层流阻力，表面阻力）成反比
• 其中空气学阻力和层流阻力受风速，空气稳定度影响较大

湿沉降

大气气溶胶粒子在参与云滴形成并在云滴增长和发展为降水过程中，被云、降水收集而随降水下落至地面

单个气溶胶粒子动力学

小尺度粒子需要从分子运动论去研究，大尺度粒子从空气动力学去研究

分子速度

假设：

• 分子尺度小于分子间距离
• 分子为球体，碰撞为弹性碰撞
• 平衡态时，分子按位置，速度的分布是均匀的
• 麦克斯韦的理想气体分子速度分布：分布函数只与温度有关
  
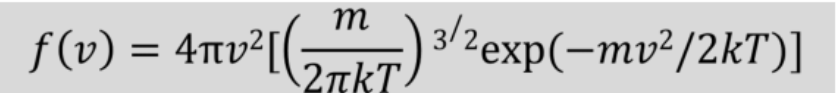
  其中最概然速度为：
  

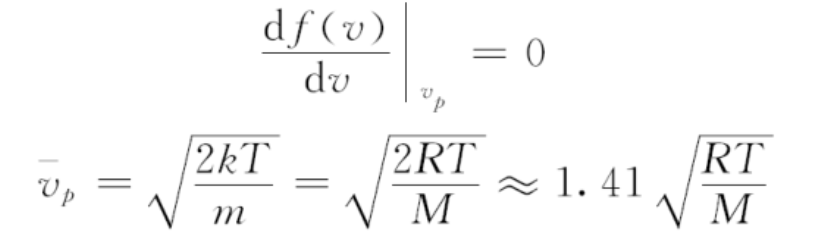
平均自由程

$\lambda$:气体分子或粒子在连续两次碰撞之间所可能经过的各段自由路程的平均值

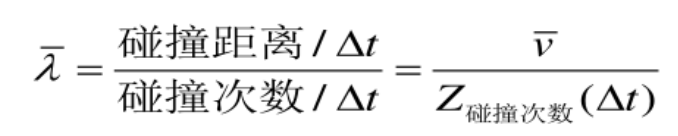
• 平均自由程与分子数密度N，分子直径d有关
  

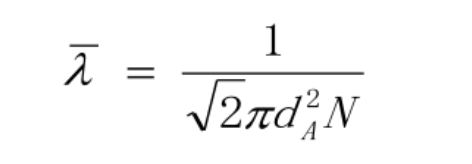
努森数

用来衡量该粒径的粒子做自由分子运动还是连续方式运动

标准大气状态下，空气分子平均自由程为0.065微米

• 粒子尺度>=0.2微米，Kn<1,粒子按连续方式运动
• 粒子尺度<0.01微米时，Kn>>1,粒子运动类似自由分子运动
• 在0.01到0.1微米的粒子，属于过渡区

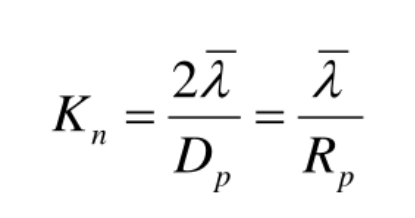
气体粘性

分子所在相邻气层具有速度梯度时，会出现速度较快的气层向速度较慢的气层传输分子动量，这种现象叫做粘性，同时伴随着气体温度的提高

热传导

相邻两个气层之间存在温度梯度时，气层之间出现能量的传输，温度高的气层向邻近温度低的气层传输分子能量

扩散

气层之间存在分子浓度梯度时，气体从浓度高的气层向邻近浓度低的气层传输分子质量
扩散系数D：用来描述一个气体分子相对其周围环境的运动能力

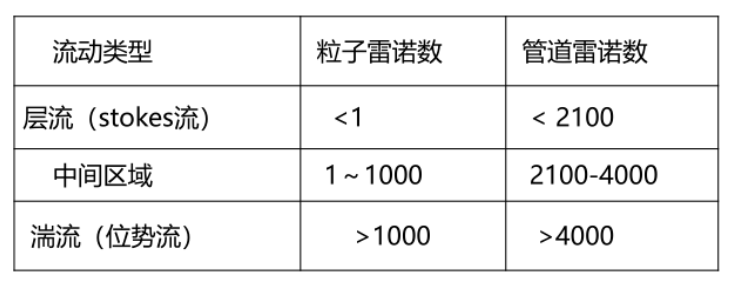
雷诺数

Re=惯性力/粘滞力,表征流体做层流运动还是湍流运动的一个无量纲数

• 当雷诺数很小的时候，说明粘性力比惯性力大，粘性力做主导，是层流
• 雷诺数很大的时候，惯性力主导，做湍流运动
• 又分为粒子雷诺数和管道雷诺数
  

管道雷诺数

$Re=\frac{\rho vd}{\mu },\rho 为流体密度，v是流体在管道中的平均速度，d是管道直径，\mu 是动力粘性系数$

粒子雷诺数

$Re=\frac{\rho vd}{\mu },\rho 为流体密度，v是流体速度，d是粒子直径，\mu 是粒子粘度$

弛豫时间

弛豫时间表示粒子调节其速度以适应新的受力状况所需时间

• 弛豫时间与粒子大小，质量，粘性系数有关，与外力大小无关

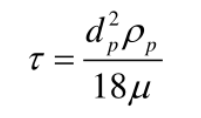
重力沉降末速度

静止空气中受重力作用做自然沉降的粒子，当重力与空气的粘滞阻力达到平衡时，重力方向上的运动速度是个恒定的下落速度，即重力沉降末速

停止距离

一个具有初速度v0的粒子，入射到静止空气中，由于空气的粘滞阻力作用，能在v0方向运动的最大距离

布朗运动

介质分子以不同方向，不同大小的力不断撞击气溶胶粒子产生，气溶胶粒子连续以不同方向，不同速度做不规则运动，随着粒子增大，撞击的次数增多，产生抵消，半径大于5微米时，布朗运动消失

• 通过对所有粒子位移的平方取平均，用它表示布朗运动的强度
• 爱因斯坦导出的准稳态下的布朗运动方程
  

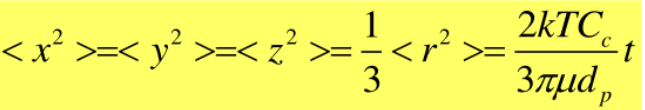
布朗扩散

气溶胶粒子受到介质分子无规则撞击做无规则运动，粒子发生从高浓度区向低浓度区的扩散，使其偏离平衡位置

• 布朗运动处处存在，但出现浓度梯度的时候布朗扩散才能起作用

菲克定律

• 第一定律：在单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量与该截面处的浓度梯度成正比——浓度梯度越大，扩散通量越大
• 第二定律：浓度随时间的变化率等于该处的扩散通量随距离变化率的负值

泳移效应

当介质分子动量分配不均匀时，通过分子动量输送，可使气溶胶粒子产生泳移

• 热力泳移：温度高的地方分子热运动速度大，可使气溶胶粒子产生由高温区向低温区的移动
• 光致泳移：介质分子吸收辐射量，因距离辐射源距离不同而产生的温差或辐射差，使粒子产生泳移
• 扩散泳移：当空气介质中某气体成分存在浓度梯度时，粒子受到浓度梯度的作用产生位移，称为扩散泳移

聚合过程

外部混合粒子群经过碰撞，黏并转变成内部凝聚体的过程

聚合方程：$dN/dt=-K_0{N}^2$ 与聚合系数和数浓度有关

布朗运动聚合

由于粒子做布朗运动导致碰撞粘并形成新的聚合体

层流聚合

层流切变聚合 气体流中，气溶胶粒子由于流体的剪切力作用而发生碰撞和聚集的过程
在层流切变聚合过程中，气溶胶粒子受到流体剪切力的作用，导致粒子之间的速度差异，由于速度差异，会发生相对运动和碰撞

• 气溶胶粒子尺度越大，层流切变聚合比布朗运动聚合更明显

湍流聚合

湍流切变聚合

是指在湍流环境下，气溶胶粒子由于湍流产生的剪切力作用而发生碰撞和聚集的过程

湍流惯性聚合

指在湍流环境下，气溶胶粒子由于湍流惯性作用而发生碰撞和聚集的过程

在湍流中，气体流体的速度和方向会随机变化，形成旋涡和涡旋结构。湍流中存在不同尺度的湍流涡旋，它们对气溶胶粒子的运动产生作用。气溶胶粒子的湍流惯性聚合主要是由于湍流涡旋的存在和湍流剪切力的影响

重力沉降聚合

受重力场影响的气溶胶粒子，尺度不同则沉降速度不同，使气溶胶粒子间出现相对运动从而产生聚合

外力场聚合

外力场可以改变粒子之间的相互作用力，从而影响粒子的聚集行为和聚集结构，比如电场，磁场，声场

一般动力学方程

框图

气溶胶光学基础

复折射指数

电磁波入射到某种物质时，因其在真空中和该物质中的传播速度不同，其传输路径会改变

• $N_{\lambda }=n_r-i{n}_i,N_{\lambda }为复折射指数，后方的实部表示物质对电磁波的散射特性，虚部表示对电磁波的吸收特性$

散射的本质

散射的本质是大气分子或气溶胶粒子在入射电磁波的作用下激发产生振动的电偶极子或多极子，一次为中心向四周辐射出与入射波频率相同的散射波

吸收系数

当电磁波通过气溶胶粒子时，单位距离的能量衰减速率

• $\beta =\frac{4\pi n_i}{\lambda }$

散射角与方位角

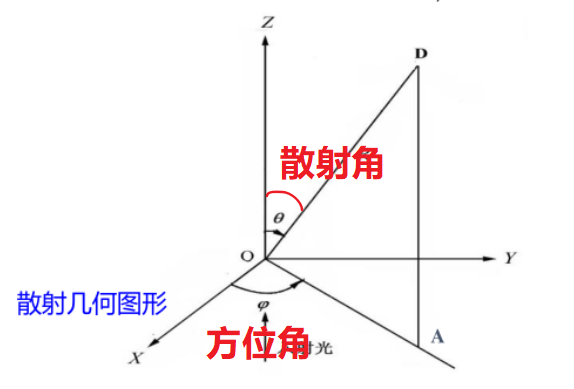
散射函数

$I(R,\theta ,\varphi )=\frac{I_0}{R^2}\sigma (\theta ,\varphi )，其中\sigma$表示散射函数，指单位光强入射时，在单位距离上测到的散射光强度

散射截面

将散射函数对4pi立体角积分，可以算出粒子散射调的总能量，而散射截面是等效的从面积为$\sigma_{sc}截取的入射光的能量

效率因子

因为一般来说，散射/吸收/消光截面与与几何截面并不相等，因此用散射效率因子=散射截面/几何截面，吸收和消光效率银子同理

相函数

表示某个方向的散射能力与平均散射能力之比

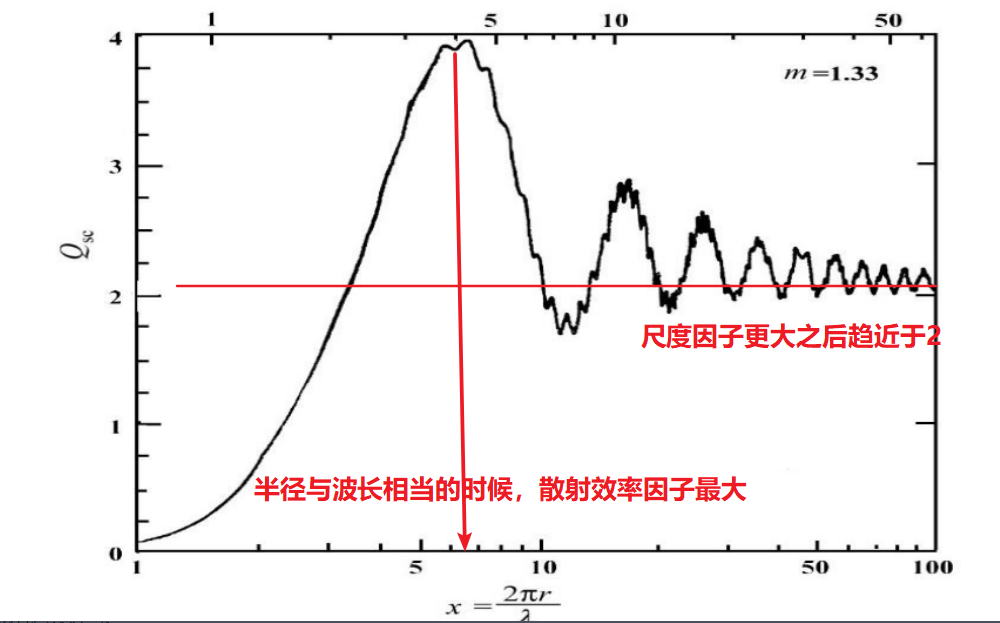
尺度因子

x=$\frac{2\pi r}{\lambda }$

• 尺度因子小于0.1，称为瑞利散射，散射光在前后半球基本是对称的
• 尺度因子大于0.1称为米散射，变为前向散射为主

单次散射反照率

散射截面/消光截面——反映了散射在总消光中的比重

非对称因子

衡量前向和后向散射的比例g取-1到1之间

瑞利散射

• 散射光强度与波长的四次方成反比
• 散射光强与半径的六次方成正比
• 入射光为自然光的时候，前后向散射呈对称分布

米散射

散射光强在各方向不对称，主要是前向散射，且随着粒子尺度抵得增大，前向散射光的占比会迅速增大

粒子群的散射

• 对一定体积中众多的散射例子而言，散射光可以射到其他粒子上，引起多次散射
• 体积消光系数：单位体积中各个气溶胶粒子的消光截面之和

比尔定律

• 上述四个因素只考虑了吸收之后简化的辐射基本方程
• 吸收中辐射强度随光学厚度e指数衰减
• 不同物质的光学厚度和直接各自光学厚度相加
• 不同物质的透过率只和就是各透过率相乘

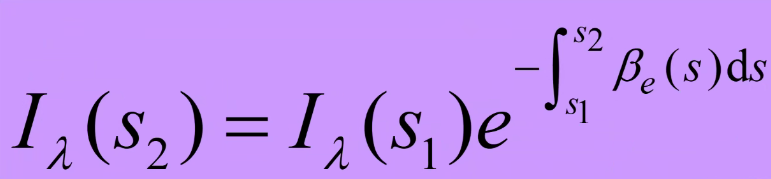
光学厚度

• 体积消光系数在一段距离的积分就是光学厚度
• 将比尔定律中的e指数衰减的幂指数（取正），就是光学厚度
  

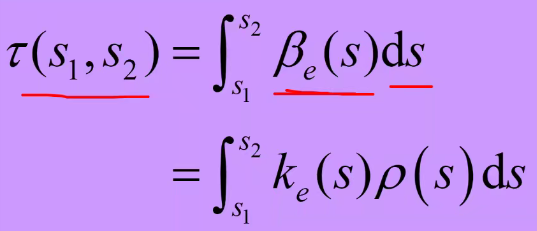
透射率

• 出射辐射强度比上入射辐射强度就是透过率

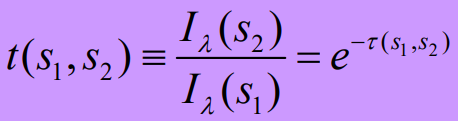
气溶胶辐射效应

在保持地表和大气状态不变的情况下，因受外部加强的某种扰动，使地球气候系统辐射能量收支发生变化，这个变化称为辐射强迫

• 通常用一段时间内平均的，单位面积上变化的辐射通量表示
• 气溶胶辐射强迫：保持地表和大气状态不变的情况，因大气成分发生变化，使地球系统辐射能量收支发生变化，这个变化的辐射通量称为气溶胶辐射强迫
• 计算：RF=（有气溶胶的入-有气溶胶的出）-（没气溶胶的入-没气溶胶的出）,RF>0加热，<0冷却

类型

直接辐射

由于气溶胶的散射特性使有无气溶胶时大气顶或地表净辐射通量发生变化

半直接辐射

由于具有强吸收性气溶胶的吸收性使有无气溶胶时大气顶或地表净辐射通量发生变化

第一间接辐射强迫

云内液态水含量不变的情况下，气溶胶粒子的增多会使云滴数浓度增加和云滴粒子减小，导致云的反照率增大

第二间接辐射强迫

云滴谱有效半径的减小将同时减少降水的形成，可能会改变云的厚度，延长云的生命期，从而导致区域平均的云反照率增加