目录
第12章 Fourier变换的性质
12.1 引言
12.2 Fourier变换性质的相关定理
12.2.1 线性定理(Linearity)
12.2.2 伸缩性定理(Scaling)
12.2.3 时间/空间平移定理(Shift)
12.2.4 频移定理
12.2.5 调制定理(Modulation)
12.2.6 微分定理(Differentiation)
12.2.7 积分定理(Integration)
12.2.8 变换的变换定理(Transform of a transform)
12.2.9 中心坐标定理(Central ordinate)
12.2.10 等效宽度定理(Equivalent width)
12.2.11 卷积定理(Convolution)
12.2.12 卷积导数定理
12.2.13 互相关性定理(Cross-correlation)
12.2.14 自相关性定理(Auto-correlation)
12.2.15 Parseval/Rayleigh定理
12.3 卷积运算(The convolution operation)
12.4 δ 函数(Delta functions)
12.5 Fourier变换的复数共轭关系
12.6 Fourier变换的对称关系
12.7 概率论和光学中的卷积例子
12.8 卷积定理的变体
第12章 Fourier变换的性质
12.1 引言
Fourier变换的威力主要源自许多描述变换操作属性的定理,这些定理提供了对物理系统属性的洞察。这些定理中的大多数都是在通信工程的背景下推导出来的,以回答诸如“如果以这样或那样的方式被操纵时间信号,则它的Fourier频率谱会发生什么样的变化?”这样的问题。因此,发展了一种思考变换操作的方式,其中Fourier变换对(Fourier transform pair) y(t)↔ Y( f ) 就像硬币的两面,一面是原始时间或空间信号,另一面是它的频谱。Fourier变换对的两侧是同一信号的互补视图,因此如果对变换对的一半执行某些操作,则必然对另一半执行某些等效操作,这是做是有某些意义的。
下面描述的定理和性质背后的许多概念在第 6 章Fourier级数的背景下进行了介绍。 在大多数情况下,这些定理可以扩展到Fourier变换的域中,只需检查随着信号观察区间的长度无限增长的极限即可。因此,这里仅列出结果就足够了。这些定理的严格证明可以在标准教科书中找到( Bracewell,1978 年;Gaskill,1978 年)。
12.2 Fourier变换性质的相关定理
12.2.1 线性定理(Linearity)
缩放函数缩放它的变换对。添加两个函数对应于添加两个频谱。即(用数学语言表达,下同),
假如 h( x )↔ H( f )
则 ah(x )↔ aH( f )----------------------------------------------[12.1]
假如 h( x )↔ H( f ), g( x )↔ G( f )
则 h(x )+ g( x ) ↔ H( f ) + G( f )------------------------------[12.2]
12.2.2 伸缩性定理(Scaling)
由因子s引起的时间/空间参考系尺度乘变化,呈反比例地伸缩函数频谱的频率轴。 例如,拉伸时间脉冲会使Fourier谱变窄且变高,因为在脉冲的增加下面积增加了。即,
假如 h( x )↔ H( f ) ,则
h( x/s )↔ | s|H( f.s ) ------------------------------------[12.3]
且
| s|h( x.s )↔ H( f/s ) ------------------------------------[12.4]
这个定理的一个简单而有用的意义在于,假如 h( x )↔ H( f ),则h( - x )↔ H(- f )。换句话说,翻转(flipping)关于原点(译注:即翻转后与原函数关于原点呈对称关系)的时间函数对应于翻转关于原点的频谱。
请注意,该定理不同于离散光谱的相应定理(图 6.3),因为纵坐标与横坐标成反比。 这是因为Fourier变换产生的是谱密度函数(a spectral density function)而不是谱幅度函数(a spectral amplitude function),因此对频率轴的刻度很敏感。
12.2.3 时间/空间平移定理(Shift)
在时间或空间上的位移(displacement)产生与频率和位移量(the amount of displacement)成正比的相移(a phase shift)。发生这种情况是因为给定的位移代表高频信号比低频信号更多的相移周期。即,
假如 h( x )↔ H( f ) ,则
----------------------------------------------------------[12.5]
12.2.4 频移定理
频率位移对应用单位相量乘以时间/空间函数,且单位向量的角度与时间/空间和位移量成正比。请注意,如果 h( x ) 是实数值,则经过频移后它将变为复数值。即,
假如 h( x )↔ H( f ) ,则
--------------------------------------------------------------[12.6]
12.2.5 调制定理(Modulation)
时间空间函数与余弦波相乘对应拆分函数的频率谱。频率的一半左移另一半右移。这只是平移定理的一种变体,这种变体使用了 Euler 恒等式关系 。即,
假如 h( x )↔ H( f ) ,则
因此,依据线性定理,推出
----------------------------------------[12.7]
调制定理是调幅无线电广播传输的基础。当低频音频信号与射频载波相乘时,音频消息的频谱被移动到电磁频谱的无线电部分,以便通过天线进行传输。类似地,一种称为超外差解调(super-heterodyne demodulation)的音频信号恢复方法涉及将接收到的信号乘以与载波频率相同的正弦波,从而解调音频分量。
12.2.6 微分定理(Differentiation)
函数的微分在频谱中引起 90°相移,并与频率成正比地缩放频谱的幅度。反复微分导致通用结果:
假如 h( x )↔ H( f ) ,则
----------------------------------------------------[12.8]
这个定理解释了为什么信号的微分有噪声操作的名声。即使信号是带限的,噪声也会引入高频信号,这些高频信号会被微分放大。(译注:在复平面上,一个变量乘以i相当于旋转90°)
12.2.7 积分定理(Integration)
函数的积分在频谱中引起 -90°相移,并与频率成反比地缩放频谱的幅度。即,
假如 h( x )↔ H( f ) ,则
+ 常量 ----------------------------------------------[12.9]
(译注:在复平面上,一个变量除以i相当于旋转 -90°,即相当于乘以 –i 。)
从这个定理我们看到积分定理类似于混淆(blurs)信号的低通滤波器。
12.2.8 变换的变换定理(Transform of a transform)
我们通常会想到使用Fourier逆变换从频谱移回时间/空间函数。然而,如果改为对频谱进行正向Fourier变换,则结果是绕 y 轴翻转的时间/空间函数。这对为什么这两个变换的内核互为复共轭给出了一些理解:逆向变换中符号的改变使函数关于 y 轴作第二次翻转(译注:即翻转后与原函数关于 y 轴呈对称关系),以便结果与原始函数匹配。即,
假如 ,则
----------------------------------------------------------------[12.10]
该定理的一个实用意义是2比1的奖励:每个成对变换都会带来第二个成对变换,而无需额外成本(译注:一对成对变换带来两对成对变换)。
假如 h( x )↔ H( f ) ,则
H( x ) ↔ h( - f ) -------------------------------------------------[12.11]
例如,rect( t ) ↔ sinc( f ) 隐含着变换 sinc ( t ) ↔ rect ( f )
这个定理强调了这样一个事实,即Fourier变换运算从根本上说是一种数学关系,可以完全脱离时间和频率的物理概念。它只是一种将一个变量的函数转换为另一个变量的函数的方法。因此,例如,在概率论中,Fourier变换用于将概率密度函数转换为矩(moment)生成函数,两者都与时域或频域没有丝毫相似之处。
12.2.9 中心坐标定理(Central ordinate)
通过与均值Fourier系数 相类比,中心坐标值H(0)(类比离散谱中的
) 表示函数h( x )下的总面积。即,
假如 h( x )↔ H( f ) ,则
对于逆变换,
------------------------[12.12]
请注意,对于实值函数 h( x ),谱的虚部将具有奇对称性,因此谱的实部下方的面积是找到 h( 0 ) 所需的全部。
例如,在光学中,线扩散函数 (LSF) 和光学传递函数 (OTF) 是Fourier变换对。 因此,根据中心坐标定理,LSF 的中心点等于 OTF 下的面积。 在二维中,变换关系指的是点扩散函数(PSF)和OTF。 在此类 2维情况下,必须对一个区域进行积分,在这种情况下,结果将解释为 2维表面下的体积。这是在频域中计算Strehl比率(译注:Karl Wilhelm Andreas Strehl (1864-4月30日-June 14, 1940-6月14日) 德因物理学家,作家和数学家)的基础。
12.2.10 等效宽度定理(Equivalent width)
中心坐标定理的一个引理是
假如 且
, 则
---------------------------------------------- [12.13]
最后一个表达式左侧的比率称为给定函数 h 的“等效宽度(equivalent width)”,因为它表示与 h 具有相同中心坐标和相同面积的矩形的宽度。 同样,右边的比率是 H 的等效宽度的倒数。因此我们得出结论,函数在一个域中的等效宽度是另一个域中等效宽度的倒数,如图 12.1 所示。 例如,当时域中的脉冲变短时,其频谱变长。 该定理量化了一种特定宽度度量的关系。

-----------------------------------图12.1 等效带宽定理------------------------
12.2.11 卷积定理(Convolution)
卷积运算(用星号表示)是一种组合两个函数以产生新函数的方法。 根据定义,
p = h * g 意味着 ---------------------------[12.14]
卷积将在第 12.3 节中详细描述。 在这里表述卷积定理就足够了:
假如 h( x )↔ H( f ),g( x )↔ G( f ) 则,
h * g = H( f ).G( f )
h.g = H( f ) * G( f ) ------------------------------------------------[12.15]
换句话说,这个定理指的是,如果两个函数在一个域中相乘,那么它们的Fourier变换在另一个域中进行卷积。与接下来描述的互相关运算不同,卷积遵循代数的交换律、结合律和分配律。即,
交换律:h * g = g * h
结合律:f * ( g * h) = ( f * g ) * h
分配律:f * ( g + h) = f * g + f * h--------------------------------------[12.16]
12.2.12 卷积导数定理
结合导数定理和卷积定理得出结论:
假如 h( x ) = f ( x ) * g( x ), 则
------------------------------------------------------[12.17]
换句话说,这个定理表明卷积的导数等于函数中的任何一个与另一个函数的导数的卷积。
12.2.13 互相关性定理(Cross-correlation)
互相关运算(用五角星表示)是一种将两个函数组合起来产生类似于卷积的新函数的方法。 根据定义,
q = h ★ g 意味着 --------------------------[12.18]
互相关定理是
假如 h( x )↔ H( f ),g( x )↔ G( f ) 则,
h ★ g ↔ H( f ). G( - f )
h( -x ) . g( x ) ↔ H( f ) ★ G( f )
h( x ) . g( x ) ↔ H( - f ) ★ G( f ) -----------------------------------[12.19]
等式 [12.14] 和 [12.16]结合在一起表明,两个函数的乘积的频谱可以用两种方式计算,
h.g ↔ H( f ) * G( f ) 和 h( x ) . g( x ) ↔ H( - f ) ★ G( f ) 。 因为函数的频谱是唯一的,这意味着,
H( f ) * G( f ) = H( - f ) ★ G( f ) ---------------------------------[12.20]
这表明了相关性和卷积之间的关系。
12.2.14 自相关性定理(Auto-correlation)
自相关定理是互相关定理的特例,当两个函数 h 和 g 是相同的函数时的互相关性。 在这种情况下,我们使用Fourier变换的Hermite对称性来证明:
假如 h( x )↔ H( f ) ,则
--------------------------------------------------[12.21]
量 h ★ h 称为函数 h 的自相关性,量 称为 h 的功率谱密度函数。这个定理指的是,自相关性函数与功率谱密度函数组成一对Fourier变换对。
12.2.15 Parseval/Rayleigh定理
在Fourier级数的背景下发展起来的Parseval能量守恒定理在Fourier变换的背景下通常被称为Rayleigh[réili]定理(译注:Rayleigh为英国物理学家)。即,
假如 h( x )↔ H( f ) ,则
-----------------------------------------[12.22]
这是为离散光谱开发的类似等式[7.6]的等式。等式左侧积分被解释为在时域中计算的信号能量总量,而右侧积分是被解释为在频域中计算的能量总量。这个模数符号(modulus symbol)(|~|) 的作用是提醒人们,被积函数通常是复数,在这种情况下,这些复数量(complex quantities)的量级(magnitude)将被积分。
Parseval的更为通用的公式如下:
假如 h( x )↔ H( f ),g( x )↔ G( f ) 则,
----------------------------------[12.23]
在许多物理解释中,函数 h 和 g 的乘积对应于瞬时或局部功率(例如,电流乘以电压,或力乘以速度),因此本定理表明,总功率可以通过对空间/时间域或频域进行积分来获得。
12.3 卷积运算(The convolution operation)
卷积是一种描述许多物理过程的数学运算,系统的响应或输出是许多单独响应叠加的结果。 例如,考虑“低通”电子滤波器对电压单位脉冲的响应,如图 12.2 所示。这种响应称为滤波器的“脉冲”响应。 低通滤波器具有输入信号的“记忆”特性,因此尽管输入仅短暂存在,但输出会持续更长的时间。因此,如果多个脉冲在不同时间到达滤波器,则滤波器将生成一系列输出波形。 如果这些输出波形的形状完全相同,无论输入脉冲何时到达,并且幅度与输入脉冲的强度成正比,则称该滤波器是时不变的(time invariant)。 现在假设输入脉冲快速连续到达,这样输出波形将开始重叠。如果实际输出波形是所有单个脉冲响应的线性和,则称该滤波器为线性滤波器(linear filter)。
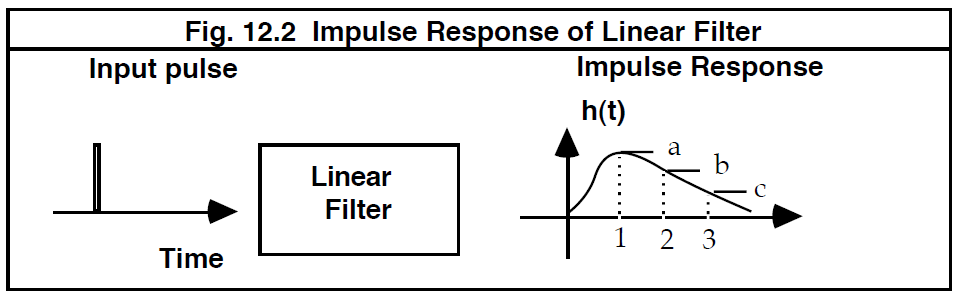
----------------------------图 12.2 线性滤波器的脉冲响应------------------------------------
图 12.3 说明了对在时间 t = 0、t = 1 和 t = 2 到达的三个输入脉冲的三个响应叠加的具体示例。 这三个输入脉冲的幅度分别为 4、5 和 6 个单位。 如果我们希望计算某个特定时刻 的响应,则可以通过三种方式进行计算。 最直接的方法是将三个脉冲响应波形适当地垂直缩放并沿时间轴移动,然后将时间
的纵坐标值相加。即,
------------------[12.24]
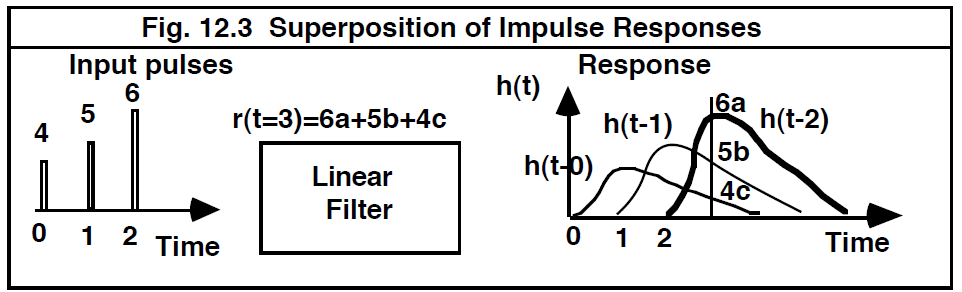
----------------------------图 12.3 脉冲响应的叠加--------------------------------------------
另外两种得到相同答案的方法对应于卷积的思想。在图 12.4 中,单位脉冲响应沿 x 轴没有位移。 在同一张图中,我们还绘制了输入脉冲,但请注意它们是以相反顺序绘制的。 然后,我们将脉冲输入序列沿 x 轴移动 量,在本例中为 3 个单位,并将结果叠加在脉冲响应之上。 现在的算法如下:依次使用每个脉冲的 x 位置,在单位脉冲响应函数上定位对应点,并按脉冲高度缩放 h( t ) 的纵坐标值。对输入序列中的每个冲击重复并添加结果。 结果将与上面等式[12.24]中给出的完全相同。

--------------------------------图 12.4 卷积方法1-------------------------------------------------
图 12.5 说明了计算特定时刻 t = 3 响应强度的等效方法。这次是时间倒转的脉冲响应。为了清楚起见,我们给这个反转函数起了一个不同的名字h',并让虚拟变量 u (dummy variable)代表反转的时间轴。 然后,这个新函数 h´(u)向右平移 3 个时间单位,并叠加在没有反转的情况下绘制的输入函数上。
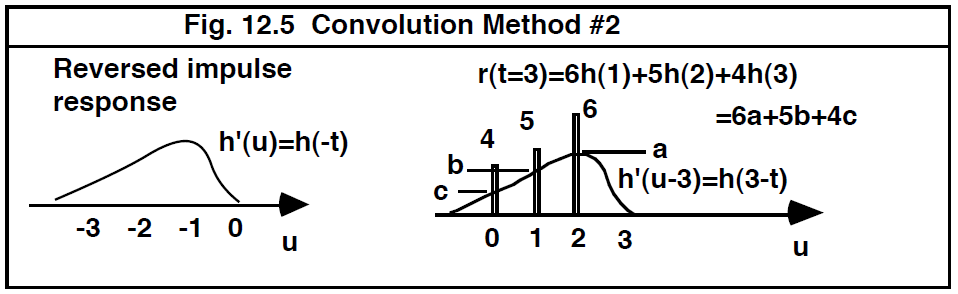
--------------------------------图 12.5 卷积方法2---------------------------------------------------
计算图 12.5 中的响应的算法与图 12.4 中的相同:将脉冲响应函数的每个纵坐标值乘以相应脉冲的幅度并将结果相加。其实这不过是一种内积。 为了看到这一点,我们将输入脉冲序列写为激励向量(stimulus vector) 并且同一时间点的脉冲响应强度可以写为向量
。 沿 u 轴绘制其操作的反转脉冲响应会将脉冲响应向量更改为
。 因此,上述用于计算时间
处的响应的方法是
----------------------------------------------------------------------[12.25]
虽然这个结果是通过 的特定例子来说明的,但同样的方法显然适用于任何时间点,所以可以删除这一点上的下标符号而不其意义。
如果我们现在将上述思想进行概括,使得输入信号是一个连续函数 s(t),那么等式 [12.25] 中向量的内积就变成了连续函数之间的内积。
-------------------------------------------------------------[12.26]
请注意,图 12.5 中的横坐标变量成为等式12.26中积分 u 的虚拟变量(译注:积分变量)。所以我们将结果识别为激励和脉冲响应的卷积。因此,我们得出结论,卷积对一组点激励的响应产生叠加。这是一个主要的结果,因为任何激励都可以被认为是点激励的集合。
如果这个结果的发展集中在图 12.4 而不是图 12.5,那么最后一个等式将是:
--------------------------------------------------------------[12.27]
由于我们观察到,无论是激励还是脉冲响应被反转和移动,都会获得相同的结果,这表明函数的顺序对于卷积来说并不重要。 即,s * h = h * s。 这是前面提到的交换律。
总之,对于线性、时间(或位移)不变系统,对任意输入的响应等于输入与系统脉冲响应的卷积。 这一结果是线性系统工程分析的基础。 因为线性系统的脉冲响应可以用来预测对任何输入的响应,它是对系统特性的完整描述。 一个等效描述是脉冲响应的Fourier变换,称为系统的传输函数(transfer function)。根据卷积定理,输入与脉冲响应的规定(prescribed)卷积等效于输入频谱与系统传输函数的乘积。由于乘法运算比卷积运算更容易被执行,因此可以在频域中进行很多分析,只有最终结果才转换回时间/空间域以进行解释。
12.4 δ 函数(Delta functions)
虽然从Fourier级数过渡到Fourier变换是一个重大进步,但也是一个退步,因为并不是所有的函数都适合进行Fourier分析。 特别是,作为Fourier级数基的正弦函数(sinusoidal functions)被发展在前的Fourier变换运算给排除了。这是因为,对于任何特定函数,其Fourier变换存在的一个前提条件是该函数是必须是“绝对可积的”,即其绝对值在 -∞ 到 +∞ 范围内的积分必须是有限的,而事实是,在时间上一直持续的正弦曲线不满足这个要求。 对于恒定信号也是如此。 另一方面,实验者遇到的任何物理信号都将在某个确定的时刻开始,并且不可避免地会在某个时刻结束。因此,经验信号(empirical signals)始终具有Fourier变换,但我们对这些信号的数学模型(mathematical models)可能不具有Fourier变换。由于函数 sin(x) 是数学模型中非常重要的元素,我们必须发挥一些独创性,想办法将它们纳入Fourier分析的领域。这正是发明δ函数的目的。
回顾一下,从Fourier级数到变换的转变伴随着观点的改变:现在,频谱是幅度密度(density)的一种体现)。因此,关注点从频谱的坐标值转向到某个带宽内频谱下的面积。 这就是为什么纯正弦波具有完美的Fourier级数表示,但无法过渡到Fourier变换:我们需要除以信号的带宽,对于纯正弦波来说带宽为零。在另一方面,如果感兴趣的重要量是变换曲线下的面积(它对应于信号中的总振幅),那么就存在有用的解决问题的办法(work-around)。这个思想就是发明一个看起来像窄脉冲(因此带宽很小)的函数,它几乎处处为零但具有单位面积。显然,当宽度趋近于零时,该脉冲的高度必须变得无限大才能维持其面积。然而,我们不应该为这个小难题(conundrum)而担心,因为我们唯一一次使用这个新函数是在积分内部,在这种情况下只有脉冲面积是相关的。这个新的函数称为单位δ函数(unit delta function),且通过以下两个条件定义:
(对于所有 t ≠ 0)
------------------------------------------------------------------[12.28]
为了表示任意其它时刻 a 的脉冲,我们写作δ( t - a) 。
该定义的一个重要结果是任意函数乘以δ函数后的积分等于原始函数上的一个点。这被称为 δ 函数的筛选属性(sifting property),发生这种情况是因为 δ 函数在任何地方都为零(除当参数为零的时候)。即,
---------------------------------------------------------------------[12.29]
其中,ε 是一个极小值。将这个结果应用到卷积积分,我们可以看到,任何函数与位于 x = a 的 δ 函数的卷积都产生一个位于 x = a 的函数
------------------------------------------------------------------------[12.30]
现在考虑δ函数的Fourier变换。根据 δ 函数的过滤属性,假如 y(x) = δ (x) ,则
-------------------[12.31]
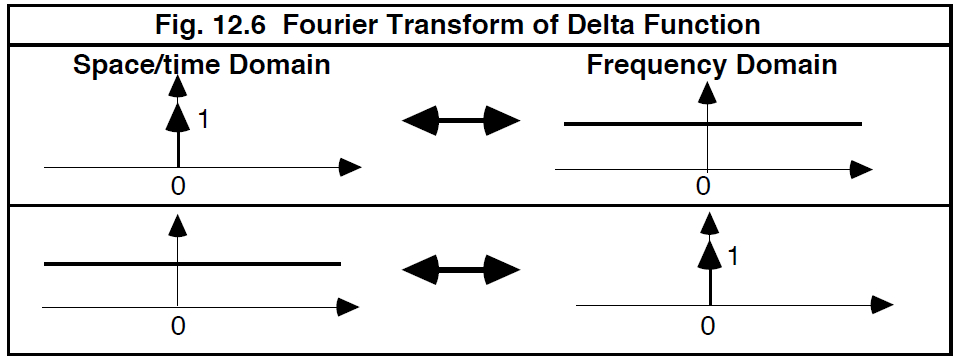
-------------------------------图 12.6 δ函数的Fourier变换-------------------------------------------
换句话说,原点处的δ 函数具有平坦的Fourier频谱,这意味着所有频率的存在程度相同。同样,单位 δ 函数在频域原点处的Fourier逆变换是一个常数(d.c. = Direct Current)值。这些结果以图形方式显示在图 12.6 中,δ函数由尖峰或箭头表示,数字表示尖峰下的面积。 由此可见,常数的Fourier变换是原点处的,δ 函数,1↔ δ(0)。将调制定理应用于此结果,我们发现余弦波或正弦波的频谱是一对δ函数,
---------------[12.32]
而反过来,δ 函数对的频谱是余弦或者正弦波,
----------------[12.33]
将 [12.15] 的卷积定理与 [12.33] 中的Fourier变换对相结合,我们可以得出结论,余弦波与时间/空间域中任何其他函数的卷积对应于给定函数的频谱乘以一对用余弦表示的δ 函数。这个乘积本身就是一对频域的δ函数。这个结果的一个重要的实际应用是余弦波通过线性滤波器总是产生余弦波。尽管滤波器可以改变余弦的幅度和/或相位,但输出仍具有正弦形状。 正弦波的这种特性称为“形式保持(preservation of form)”,极大地简化了表征滤波器效果的任务,这也是将线性滤波器的输入/输出关系表征为增益和相位传输函数的自然选择的主要原因。

----------------------------图12.7 余弦函数的Fourier变换-------------------------------
12.5 Fourier变换的复数共轭关系
如果对一个函数取复共轭,则它的频谱反映在原点附近。表 12.1 总结了这一表述和相关结果。

----------------------------表12.1 Fourier变换的复数共轭关系-------------------------------
12.6 Fourier变换的对称关系
在第5章中我们看到,任何函数都可以写成奇函数和偶函数之和 y(x) = E(x) + O(x),通常,E(x) 和 O(x) 是复数值。将这个事实应用到Fourier变换的定义就产生
----------------[12.34]
从中我们可以推导出表 12.2 中空间/时间域中的函数 y(x) 与其Fourier谱 𝖸( f ) 之间的对称关系。这些关系的图形说明可以在第 2 章中关于Bracewell (1978)的部分找到。 对称关系是二维函数的一个更丰富的主题,因为对称性可能存在于 𝗑 轴,或 𝗒 轴,或两者。
使用对称关系的一个实际例子是根据Fourier谱 𝖸( f ) 计算实值函数 y(x) 的中心坐标 y (0)。 根据表 12.2,在非对称 y(x) 的一般情况下,频谱 𝖸( f ) 是具有Hermite对称性的复数值(实部为偶数,虚部为奇数)。 由于奇函数下的面积为零,因此中心坐标 y (0) 减少到 𝖸( f ) 的实部下的面积。 该定理的二维版本是计算点扩散函数的光学图像质量Strehl比率度量的基础,该点扩散函数使用光学传输函数中可用的频域信息计算。

----------------------------表12.2 Fourier变换的对称关系------------------------------
12.7 概率论和光学中的卷积例子
概率论的一个著名定理指出,如果 𝖷 和 𝖸 分别是具有相关概率密度函数 和
的独立随机变量,则存在一个等于 𝖷 和 𝖸 之和的新的随机变量 𝖹 ,其概率密度函数等于其构成成分的概率密度函数的卷积,即,
。 这种卷积可以在频域中进行,方法是乘以组成密度函数(称为“特征函数”)的Fourier变换,然后对乘积进行逆变换。 此外,𝖹 的方差是 𝖷 和 𝖸 的方差之和。因此从这个例子中得出一个简单的规则:两个概率密度函数的卷积导致它们的方差相加。
在光学中,局部物体的图像等于物体在二维空间中的辐射分布与光学系统的点扩散函数(PSF)的卷积。 PSF 是点源的图像,因此是成像系统的脉冲响应。定义对象的强度分布的方差是对象大小的度量。同样,PSF的方差是其大小的度量。 因此,图像的大小是对象大小与 PSF大小的总和。 这样,光学成像可以被认为是一种模糊操作,它使图像的大小超过物体的大小,其大小等于 PSF的大小。 Bracewell (1978) 提到了对一维函数卷积的这种解释,并被 Nam 等人扩展到二维。 (2011) 使用径向方差作为尺寸概念二维的自然扩展。 强度分布 I(𝗑, 𝗒) 的径向方差 V 定义为关于质心 在径向方向上的二阶矩,并在笛卡尔坐标系中计算为
------------------------------[12.35]
12.8 卷积定理的变体
在等式[12.15]的基本卷积定理 h * g = H( f ).G( f ) 和等式[12.19]的相关性定理 h( x ) ★ g( x ) ↔ H( f ) G( - f )中,当我们允许变量的复数共轭和符号反转的时候,它们呈现不同的形式。见表12.3中的总结。速记符号(short-hand notation) h( - )指的是h( - x )(即,函数已经绕原点左右翻转), h* 表示复数h的共轭。
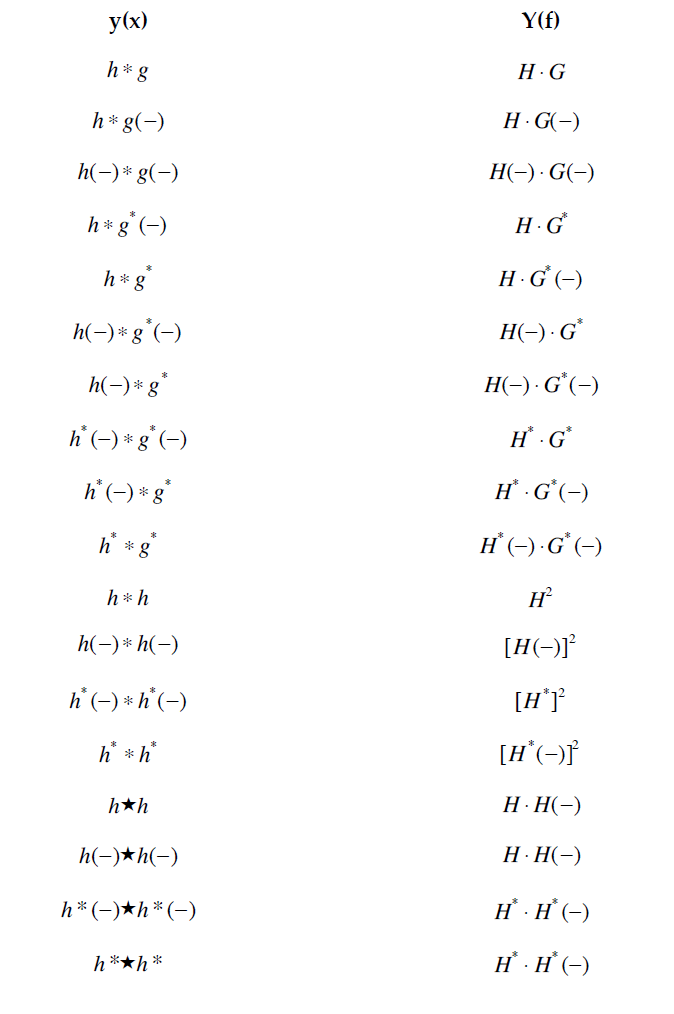
----------------------------表12.3 Fourier变换的卷积和相关性关系--------------------------
内容来源:
<< Fourier Analysis for Beginners>> Larry N. Thibos