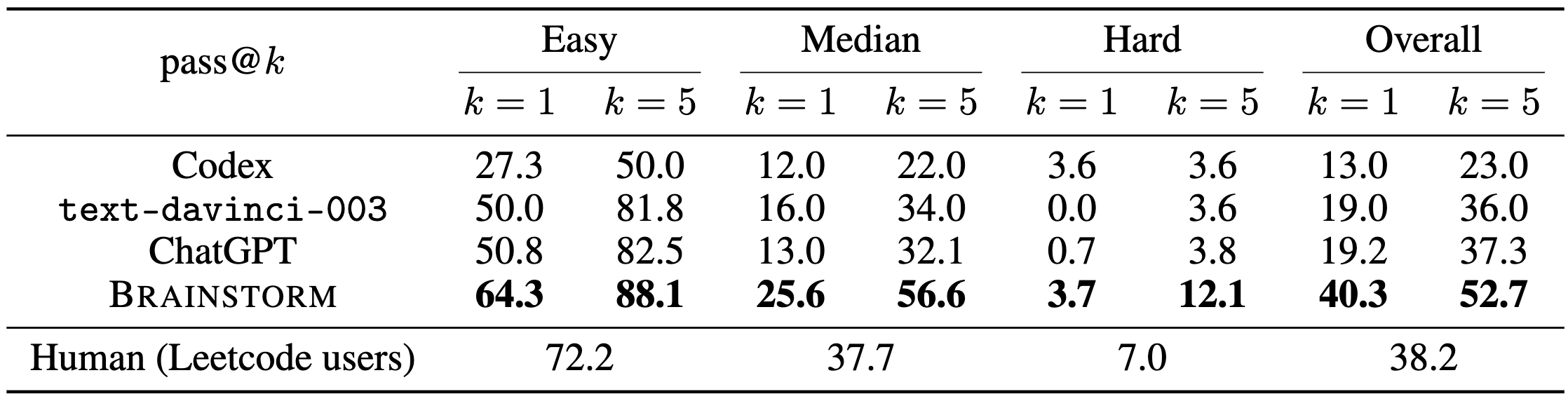
目标检测是计算机视觉领域中的一个重要问题，它需要从图像或视频中检测出物体的位置和类别。近年来，深度学习技术在目标检测领域取得了显著的进展，其中一个重要的方法是基于YOLO（You Only Look Once）算法的目标检测。

YOLO算法的优点是速度快，但是在检测小物体和密集物体方面存在一定的问题。因此，本文将介绍一些改进的YOLO目标检测方法，以提高其性能和效率。

一、多尺度训练

YOLO算法将输入图像分成S x S个网格，并在每个网格中预测B个边界框和每个边界框的类别概率。然而，如果物体的尺寸很小或者位于图像的边缘位置，可能会被错误地检测或者无法检测到。因此，我们可以通过在训练时使用多个尺度的图像来改进YOLO算法的性能。

具体来说，我们可以在训练时随机地对输入图像进行缩放，使其具有不同的大小和比例。这样，模型就可以学习到不同尺度下的物体特征，并且可以更好地适应不同大小和比例的物体。这个方法在改进YOLO算法的性能方面有很好的效果。

二、注意力机制

注意力机制是一种常见的深度学习技术，它可以帮助模型关注图像中的重要区域，从而提高目标检测的准确性。在YOLO算法中，可以使用注意力机制来增强模型对小物体和密集物体的检测能力。

具体来说，我们可以使用注意力机制来加权不同特征图的信息，从而使模型更关注某些特定的区域。例如，在YOLOv4算法中，使用了一个基于SENet的注意力机制，它能够自适应地调整特征图的权重，从而提高模型对小物体和密集物体