题目

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

2 <= n <= 58

解题思路

令 xxx 是拆分出的第一个正整数，则剩下的部分是 n−xn-xn−x，n−xn-xn−x 可以不继续拆分，或者继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积，因此可以使用动态规划求解。

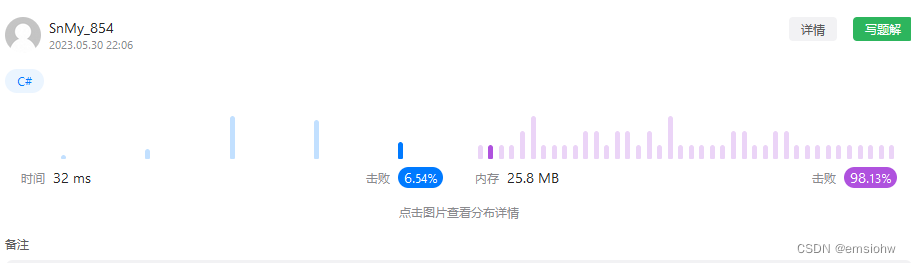
public class Solution 
{
    public int CuttingRope(int n) 
    {
        int[] dp = new int[n+1];
        for(int i = 2;i<=n ; i++)
        {
            int currentMax = 0;
            for(int j = 1; j<i; j++)
            {
                currentMax=Math.Max(currentMax,Math.Max(j*(i-j),j*dp[i-j]));
            }
            dp[i] = currentMax;
        }
        return dp[n];
    }
}

优化

翻到一个有意思的题解：
规则1，在质数中（不可由其他数组合乘积得到），只有3比其组合乘积大。比如 5 ,2 * 3 = 6比5大。
根据这个规则定下优先分配3。
但由于题目一定要分配成至少两个数，所以在n小于5的时候，有一点区别。 n < 4 时，1、2、3都无法由其他数字组合乘积得到，所以返回n-1。 n == 4 时，其组合数22比31大。
乘法中1无意义，3组合1等于无意义组合，因此弱于2*2 。 因此另一个规则是，优先分配成两个大于1的数。由于这个规则只适用于4，所以直接特殊处理了。

作者：煎蛋的少年
链接：https://leetcode.cn/problems/jian-sheng-zi-lcof/solutions/1318376/zai-zhi-shu-zhong-zhi-you-

学习的时候注释一下看懂代码ヾ(◍°∇°◍)ﾉﾞ

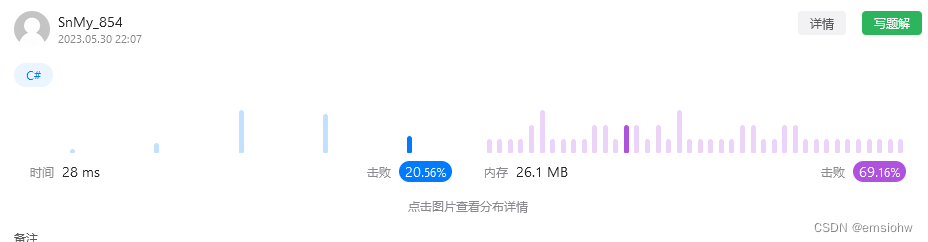
public class Solution {
    public int CuttingRope(int n) 
    {
        //特殊情况
        if (n < 4)
        {
            return n - 1;
        }
        //特殊情况
        if (n == 4)
        {
            return 4;
        }
        int res = 1;
        //只存在为res = 3*3*3*~*(3-3n)这种情况
        while (n >= 5)
        {
            n -= 3;
            res *= 3;
        }
        return res * n;
    }
}