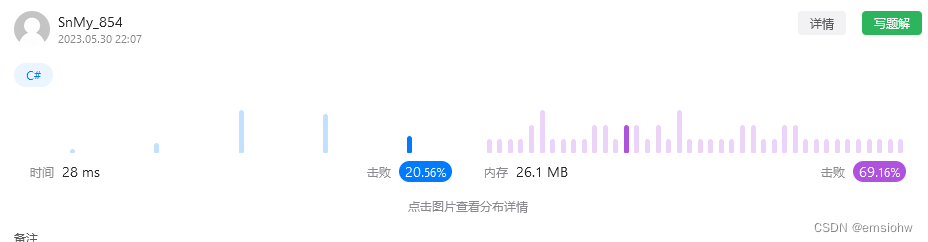
最近做了两套笔试题,复习一下错题,有很多地方需要查缺补漏,再谈一下感受总结一下。
2018届吉比特校招技术类笔试B卷
吉比特2018届提前批校园招聘-开发类试卷
一、基础题
1.已知 a = 6789x + 6789、b = 6789x + 6790、c = 6789x + 6791,则代数式a² + b² + c²-ab -bc -ca 的值为________。
题目简单,完全平方公式逆运算,1/2*[(a-b)2+(b-c)2+(c-a)2]即为原式,(1/2)[(-1)2+(-1)2+(2)2]=3。当时怎么没看到平方,直接1/2*4=2。
正确答案:3
2.两个圆,半径分别为1cm、3cm,小圆在大圆外,绕大圆圆周滚动一周,请问小圆一共旋转了几圈?
题目简单,实际上,可以看到圆心经过的距离,3+1=4。当时想着总路程3,每一圈经过1,呆了。
正确答案::4
3.假定一个同步总线的工作频率16MHz ,总线中有 32 位数据线,每个总线时钟传输一次数据,则该总线的最大数据传输率为________。
16 * 1 000 000 * 4B / 1s = 64 MB/s 。当时只知道32位数据线是4个字节。
正确答案:64MB/s
4.长度为1米的细绳上系有小球,从A点处放手后,小球第一次摆到最低点B处共移动了________米?
A 1 +(π/3) B1 + (2π/3) C2π/3 D1/2 +(π/2)
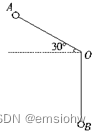
先是自由落体运动 AA’为一竖直线垂直于水平线 OA=OA’ ,然后做圆弧运动。
正确答案:1 +(π/3)
二、真·基础题(牢记概念题)
1.怎样遍历二叉查找树可以得到一个从小到大的有序序列?
正确答案:中序遍历。
2.下列哪个排序算法不是稳定的
A冒泡排序 B选择排序 C插入排序 D归并排序
正确答案:选择排序
3.给定一组数:71、39、80、25、50、42、91。对其进行排序操作,排序过程中出现如下顺序:42、39、50、25、71、80、91。那么可能使用的是哪种排序算法________。
A归并排序 B快速排序 C插入排序 D选择排序
正确答案:快速排序
4.10个并发进程使用同一个共享变量,如果最多允许4个进程同时进入其临界区,则互斥信号量的变化范围应是
正确答案:4,3,2,1,0
5.红黑树的插入复杂度为
正确答案:O(log2(n))
6.如果只想得到5000个元素组成的序列中第10个最小元素之前的部分排序的序列,使用下列选项中的哪种方法最快?
A归并排序 B快速排序 C堆排序 D选择排序
正确答案:堆排序
7.对初始序列18625473采用堆排序,当建堆(小顶堆)完毕时,堆所对应的二叉树中序遍历序列为________。
堆排序后
1
2 4
3 5 6 7
8
中序:左根右
正确答案:83251647
8.给定一个m行n列的整数矩阵,每行从左到右和每列从上到下都是升序的。判断一个整数k是否在矩阵中出现的最优算法在最坏情况下的时间复杂度是________。
正确答案:O(m+n)
9.设高度为h(只有根结点时,h=1)的二叉树没有度为1的结点,则该二叉树的总结点数至少为________。
满足题意的二叉树除了根节点外,每层只有两个结点,连在同一个父亲下,于是答案为 2h-1
正确答案: 2h-1
三、编程题
1.求素数
输入M、N,1 < M < N < 1000000,求区间[M,N]内的所有素数的个数。素数定义:除了1以外,只能被1和自己整除的自然数称为素数
using System;
public class Program {
public static void Main() {
string line;
while ((line = System.Console.ReadLine ()) !=
null) { // 注意 while 处理多个 case
string[] tokens = line.Split();
int m = int.Parse(tokens[0]);
int n = int.Parse(tokens[1]);
int Count = 0;
for(;m<n;m++)
{
if(IsPrimeNum(m))
Count++;
}
System.Console.WriteLine(Count);
}
}
public static bool IsPrimeNum(int n)
{
//3以内的数
if (n <= 3) return n > 1;
//位与 判断是否为偶数
if ((n & 1) == 0) return false;
//大于5的素数与6的倍数相邻,例如7,11,13,17,注意不是与6相邻就是素数!
if (n % 6 != 1 && n % 6 != 5) return false;
//在n的开放到5之间查找
//tip:由 a=bc=sqrt(a)*sqrt(a)
//可推出==> b、c中有一个大于sqrt(a)一个小于sqrt(a)
//或两个都等于sqrt(a)
int sqrt = (int)Math.Sqrt(n);
//步进为6进行查找
for (int i = 5; i <= sqrt; i += 6)
{
if (n % i == 0 ||n % (i + 2) == 0) return false;
}
return true;
}
}
2.两个整数二进制位不同个数
输入两个整数,求两个整数二进制格式有多少个位不同
public class Program {
public static void Main() {
string line;
while ((line = System.Console.ReadLine ()) != null)
{ // 注意 while 处理多个 case
string[] tokens = line.Split();
int x = int.Parse(tokens[0]);
int y = int.Parse(tokens[1]);
int cnt = 0;
//遍历两个整数的二进制位,每次比较它们的二进制位的最低位(即末位),并统计不同位数的数量
while (x != 0 || y != 0)
{
//当最后一位相同时,异或的结果为0;当最后一位不同时,异或的结果为1。
cnt += (x & 1) ^ (y & 1);
x >>= 1;
y >>= 1;
}
System.Console.WriteLine(cnt);
}
}
}
三、其他知识点
1、C语言类型转换分级别,一般多是:默认状态:低级向高级转换,级别高低小到大int、float、double注意char只可以和int之间转换;
2、若要高级向低级转换:就要用到强制类型转换符;
3.快速排序 、冒泡排序 、直接插入排序 、堆排序,除了堆排序算法的比较次数是O(nlog2n),其他的都是n(n-1)/2;