假设一个简单的案例

投入的广告费越多，广告的点击量就越高，进而带来访问数的增加，不过点击量经常变化，投入同样的广告费未必能带来同样的点击量。根据广告费和实际点击量的对应关系数据，可以将两个变量用下面的图展示出来。

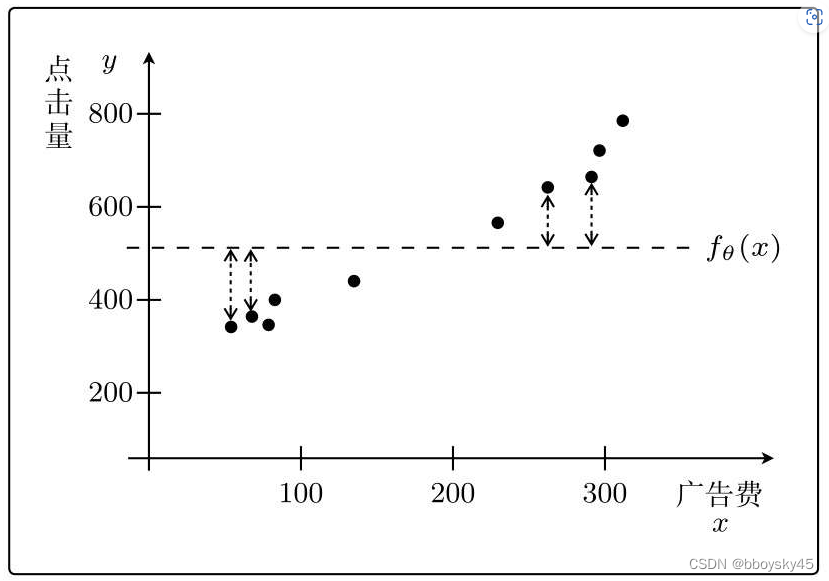
如上图，如果花了200日元的广告费，广告的点击量大概是500次左右。这就是机器学习，从数据中进行学习，然后给出预测值。

应用机器学习里的回归算法。

把图想象为函数。只要知道通过图中各点的函数的形式，就能根据广告费得知点击量了。不过刚才我也说过，点击量经常变化，这叫作“点击量中含有噪声”，所以函数并不能完美地通过所有的点。

 假设我们使用一次函数来表达广告费和点击量的关系，则表达式是：

其中a是斜率、b是截距；x是广告费、y是点击量。

比如我们设   那么表达式变为 

计算一下x=100时y的值，100日元的广告费带来的点击量为201左右。

 看一下刚才的图，如果广告费为100日元，那么点击量应该大于400。

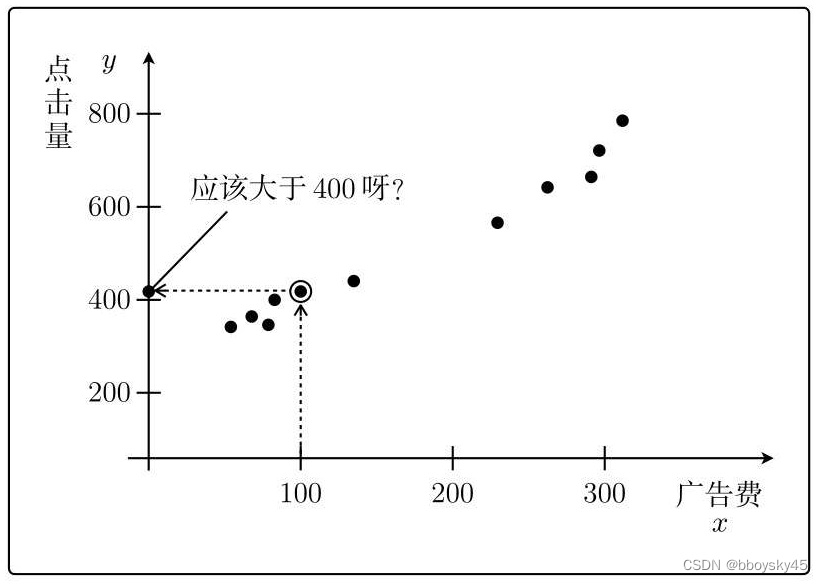
这说明我们刚才确定的参数  完全不正确。

接下来我们就要使用机器学习来求出正确的  和  的值。

最小二乘法

上面随便确定了一个参数，得到了形式为 的表达式，将广告费的值代入这个中进行计算。

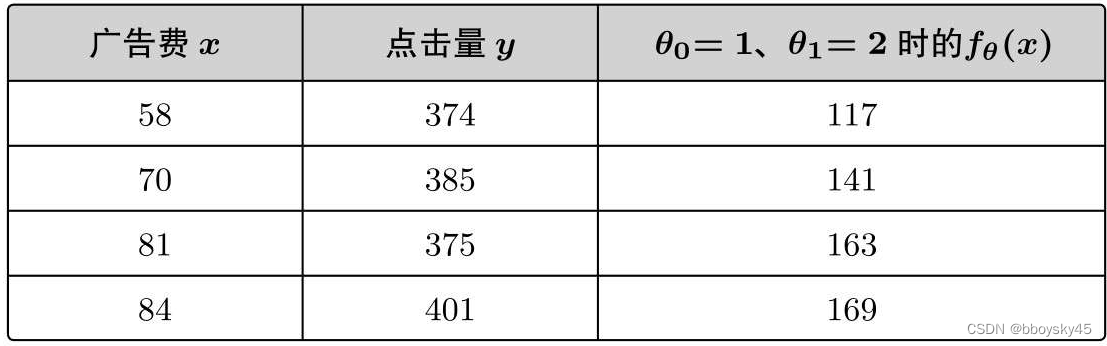
与的值完全不同。理想的情况就是二者一致，也就是，我们的目标是让误差最小。可是，让所有点的误差都等于0是不可能的，数据中包含噪声。

图中的虚线箭头表示训练数据的点和  的误差。

只要想办法缩小误差虚线的高度，就能预测正确的点击量了。所以问题的关键在于减小误差！

目标函数

假设有n个训练数据，那么它们的误差之和可以用以下表达式表示。这个表达式称为目标函数，的E是误差的英语单词Error的首字母。

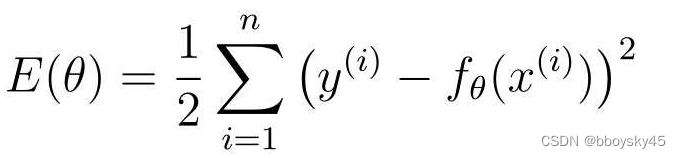 公式白话：对每个训练数据的误差取平方之后，全部相加，然后乘以1/2。

为什么要计算误差的平方呢？

 如果只是简单地计算差值，就得考虑误差为负值的情况。比如的图像是这样的，这种情况下，中间以左的误差是负数，以右的误差是正数，二者相加正负相抵，计算误差之和结果会是接近0的数。误差之和虽然为0了，但是很明显这个水平方向的是不对的。

实际来计算一下的值。设，将刚才列举的4个训练数据代入表达式。求出来的误差有点大，

 

112176.5这个值本身没有什么意义，我们要修改参数θ，使这个值变得越来越小，这种做法称为最小二乘法。

目标是要让越来越小，不过一边随意修改的值，一边计算并与之前的值相比较的做法实在是太麻烦了。使用微分来解决这个问题。

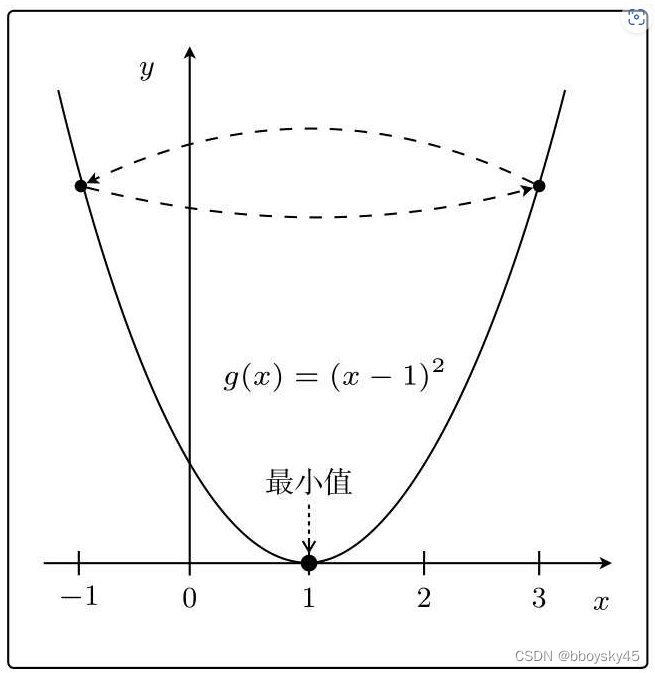
用简单的例子来说明；比如有一个表达式为的二次函数，它的最小值是g(x)=0，出现在x=1时。这个二次函数的增减表是什么样呢？

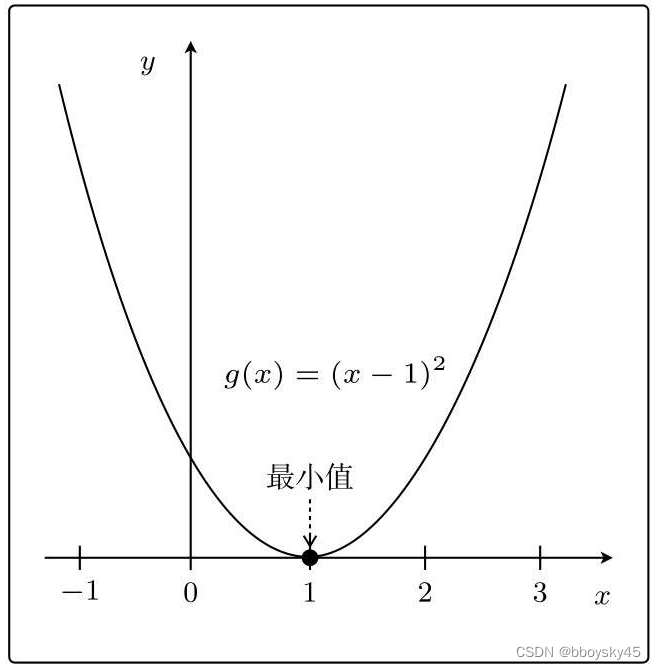
首先微分对吧？将g(x)展开，有 

 所谓导数，就是微分后的函数，只要看2x-2的符号就行了，所以增减表是这样的。

 根据这张增减表可以知道，在x＜1时，g(x)的图形向右下方延伸，反之当x＞1时，g(x)的图形向右上方延伸，换句话说就是从左下方开始延伸的。

 比如在x=3这一点，为了使g(x)的值变小，我们需要向左移动x，也就是必须减小x。

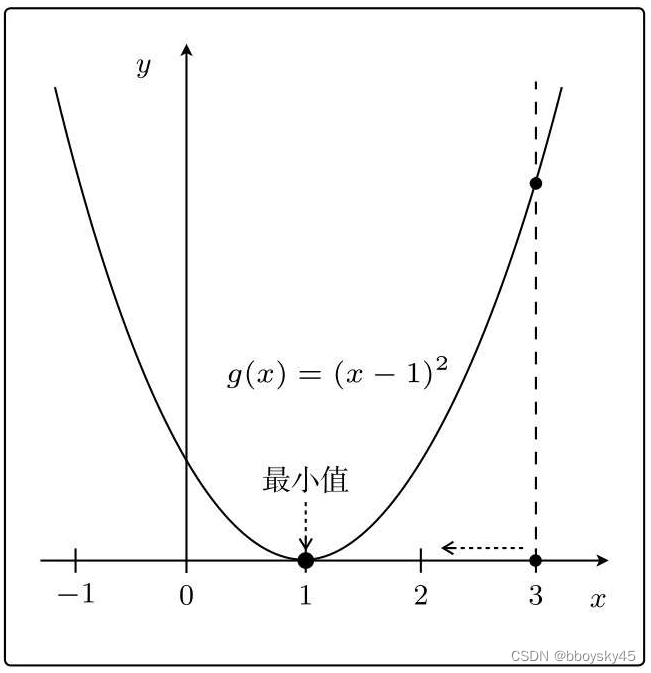
只要向与导数的符号相反的方向移动x,g(x)就会自然而然地沿着最小值的方向前进了。

 这也被称为最速下降法或梯度下降法。用以下公式定义：

公式表示用上一个x来定义新的x。

 η是称为学习率的正的常数，读作“伊塔”。根据学习率的大小，到达最小值的更新次数也会发生变化。换种说法就是收敛速度会不同。有时候甚至会出现完全无法收敛，一直发散的情况。

比如η=1，从x=3开始,g(x)的微分是2x-2，那么更新表达式就是x:=x-η(2x-2)

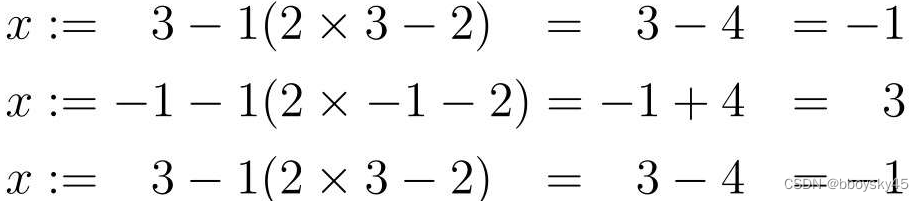
一直在3和-1上跳来跳去，就陷入了死循环。

那设η=0.1，同样从x=3开始，这次渐渐接近x=1了：

回过头来看一下目标函数：

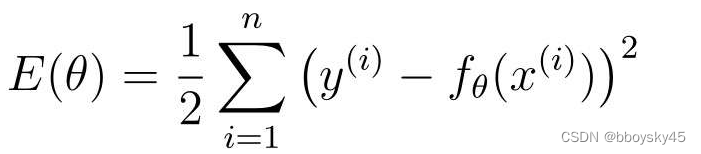
这个目标函数和刚才例子中的g(x)同样是开口向上的形状，所以刚才讨论的内容也同样适用于它。不过这个目标函数中包含，从表达式2.3.1又可以看出，拥有和两个参数。也就是说这个目标函数是拥有和的双变量函数，所以不能用普通的微分，而要用偏微分，即复合函数的微分。

中有，而中又有，假设：

则：

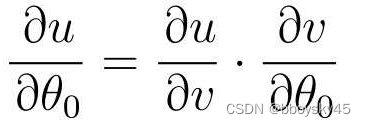
先求u对v微分：

最后一行，常数与  相抵消了，这就是一开始乘以  的理由。

再来求 v对的微分：

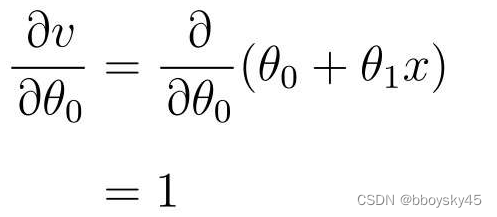
则参数的求解公式如下：

 用相同的方法再算一下对微分的结果：

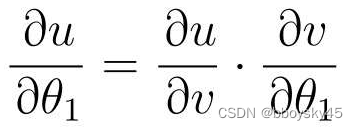
 参数和的更新表达式就是这样的：

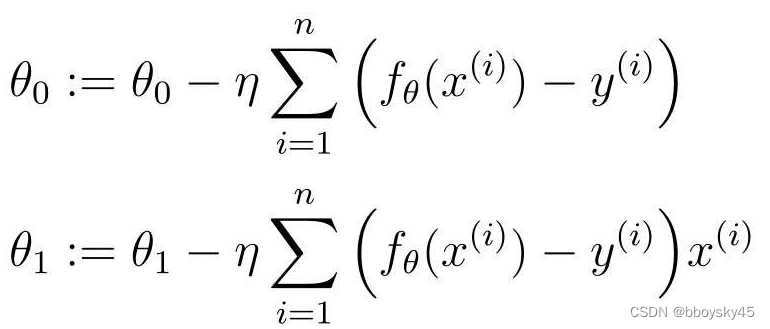
最后，只要根据这个表达式来更新和即可。