文章目录
- 1 线性回归
- 1.1 定义
- 1.2 题目分析
- 1.3 误差项分析
- 1.4 目标函数推导
- 1.5 线性回归求解
- 1.6 最小二乘法的参数最优解
- 2 目标函数(loss/cost function)
- 3 模型效果判断
- 4 机器学习调参
- 5 梯度下降算法
- 5.1 梯度方向
- 5.2 批量梯度下降算法(BGD)
- 5.3 随机梯度下降算法(SGD)
- 5.4 BGD和SGD算法比较
- 5.5 小批量梯度下降法(MBGD)
- 5.6 梯度下降法—调优策略
- 5.7 BGD,SGD,MBGD的区别
- 6 梯度下降与最小二乘(正规方程)的区别
- 7 用法(梯度下降、坐标轴下降法)
- 8 线性回归的扩展
- 9 线性回归总结
- 10 局部加权回归—直观理解
- 10.1 局部加权回归—权重值设置
1 线性回归
Logistic回归:线性回归分析模型
Softmax回归:逻辑回归
梯度下降
特征抽取
线性回归案例
1.1 定义
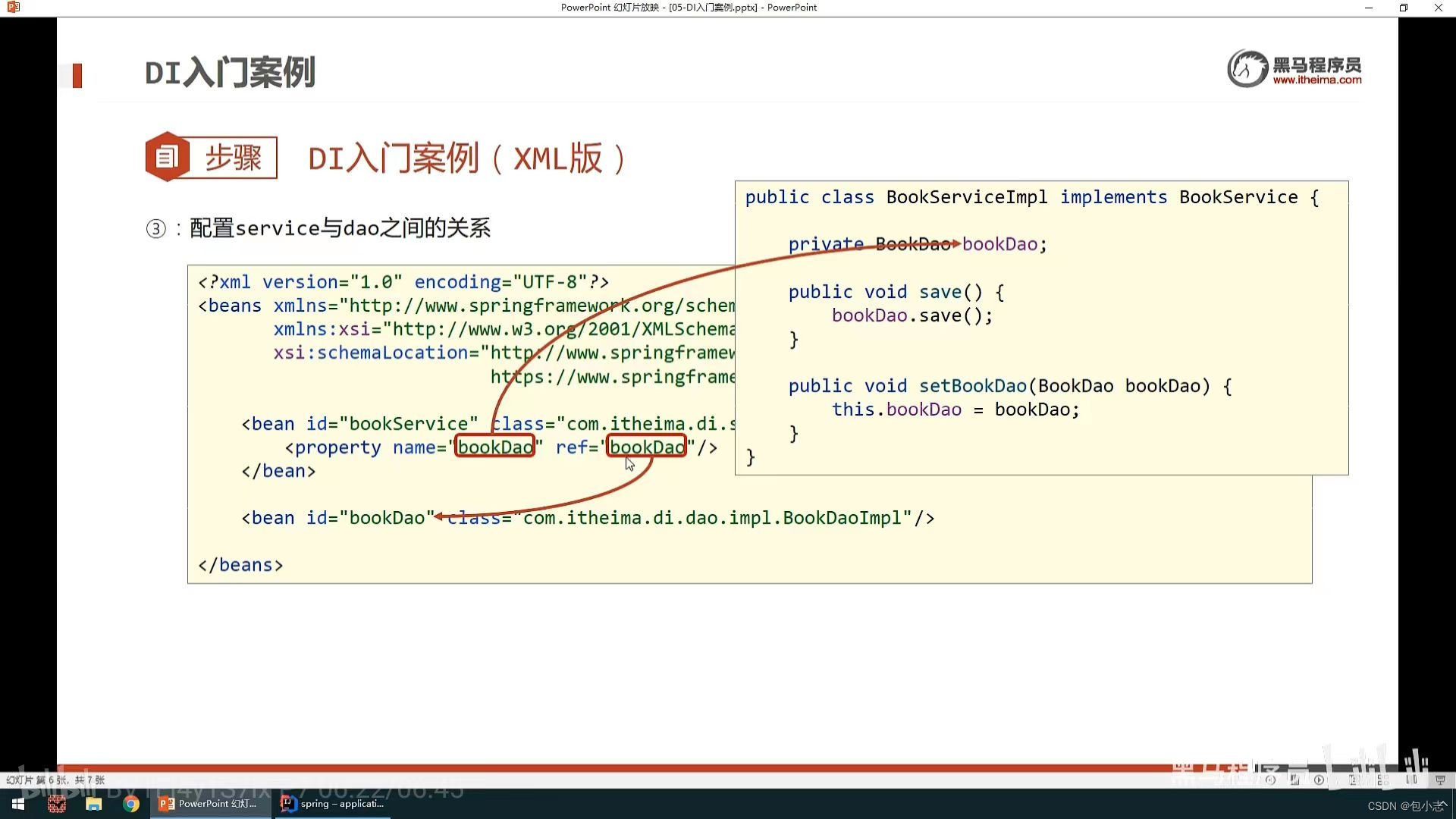
定义:线性回归通过一个或者多个自变量与因变量之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合
- 从机器学习的角度来讲,用于构建一个算法模型(函数)来做属性(X)与标签(Y)之间的映射关系,在算法的学习过程中,试图寻找一个函数h:Rn->R使得参数之间的关系拟合性最好。
- 回归算法中算法(函数)的最终结果是一个连续的数据值,输入值(属性值)是一个d维度的属性/数值向量
优点:结果易于理解,计算不复杂
缺点:对非线性的数据拟合不好
适用数据类型:数值型和标称型
一元线性回归:涉及到的变量只有一个
多元线性回归:涉及到的变量两个或两个以上
1.2 题目分析
- 数据:工资和年龄(2个特征)
- 目标:预测银行会贷款给我多少钱(标签)
- 考虑:工资和年龄都会影响最终银行贷款的结果那么它们各自有多大的影响呢?(参数)
| 工资(X1) | 年龄(X2) | 额度(y) |
|---|---|---|
| 4000 | 25 | 20000 |
| 8000 | 30 | 70000 |
| 5000 | 28 | 35000 |
| 7500 | 33 | 50000 |
| 12000 | 40 | 85000 |
解释:
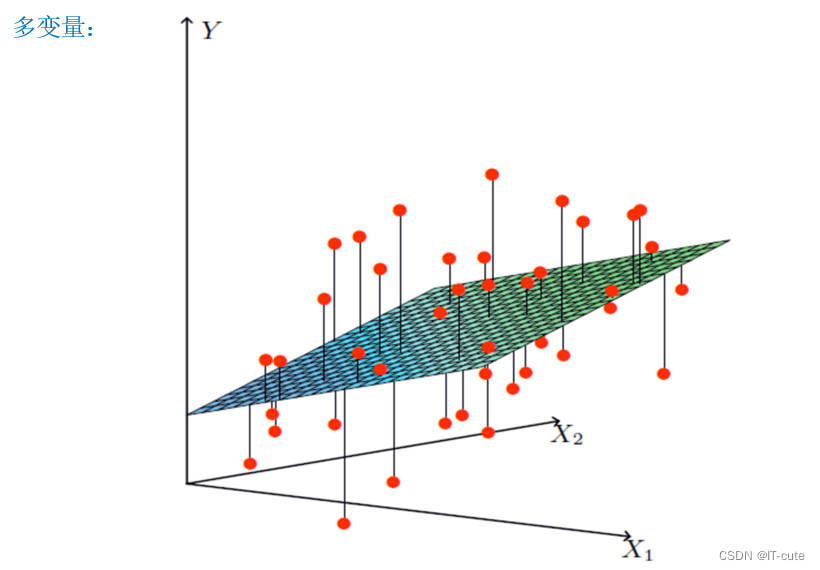
- 假设X1,X2就是我们的两个特征(工资,年龄),Y是银行最终会借给我们多少钱
- 线性回归呢就是找到最合适的一条线(想象一个高维)来最好的拟合我们的数据点,那么这个地方因为自变量涉及两个,所以最终目的就是找出一个拟合平面。
求解:
- 假设θ1是工资的参数, θ2是年龄的参数。
- 拟合的平面:(θ0是偏置项,θ1,θ2为权重)
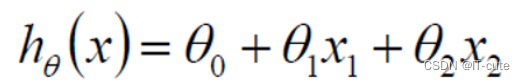
- 整理得:

1.3 误差项分析
-
y(i)为第i个训练样本的真实值
-
hθ(xi)为第i个训练样本特征值组合预测函数
-
真实值和预测值之间肯定是要存在差异的(用 ε 来表示该误差)
-
对于每个样本来说,真实值等于预测值加上误差值
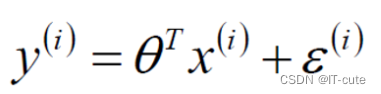
- 误差ε(i)是独立并且具有相同的分布,并且服从均值为0方差为θ2的高斯分布(正态分布)。(独立同分布)注意是假设。(原因:中心极限定理)
- 独立:张三和李四一起来贷款,他俩没关系。
- 同分布:他俩都来得是我们假定的这家银行(比如中华银行)。
- 高斯分布:银行可能会多给,也可能会少给,但是绝大多数情况下这个浮动不会太大,极小情况下浮动会比较大,符合正常情况。
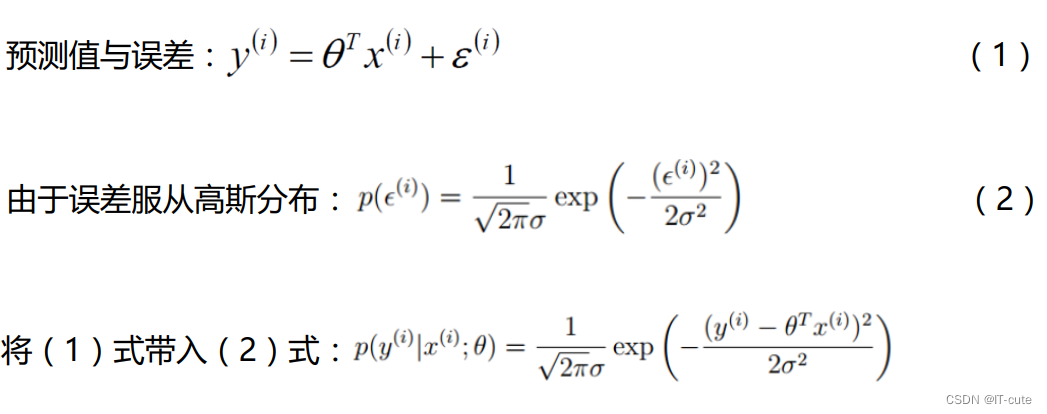
1.4 目标函数推导
最小二乘法是用似然函数一步步估计得来的。

1.5 线性回归求解

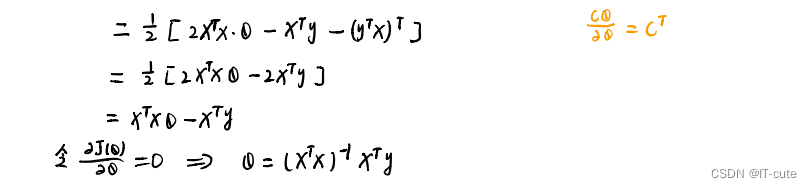
1.6 最小二乘法的参数最优解

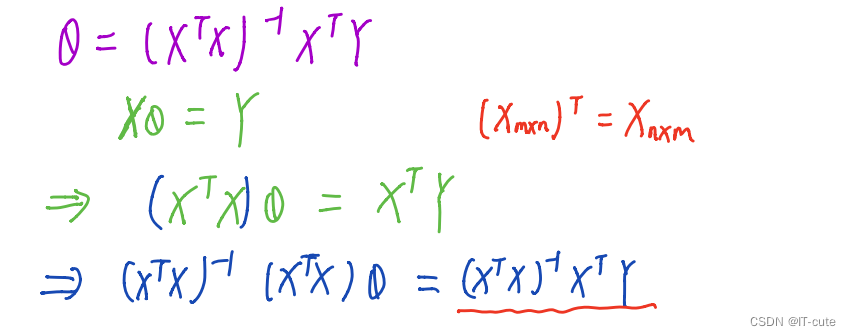
X为特征值矩阵,y为目标值矩阵
缺点:当特征过于复杂,求解速度太慢
对于复杂的算法,不能使用正规方程求解(逻辑回归等)
2 目标函数(loss/cost function)
目标函数或者损失函数越小越好。

3 模型效果判断
- MSE:误差平方和,越趋近于0表示模型越拟合训练数据。
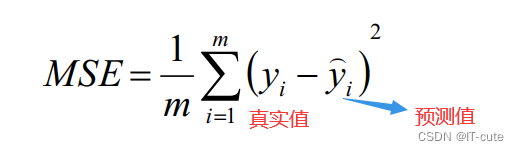
- RMSE:MSE的平方根,作用同MSE
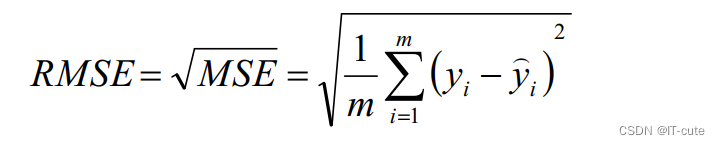
- R2:取值范围(—∞,1],值越大表示模型越拟合训练数据;最优解是1;当模型预测为随机值的时候,有可能为负;若预测值恒为样本期望,R2为0
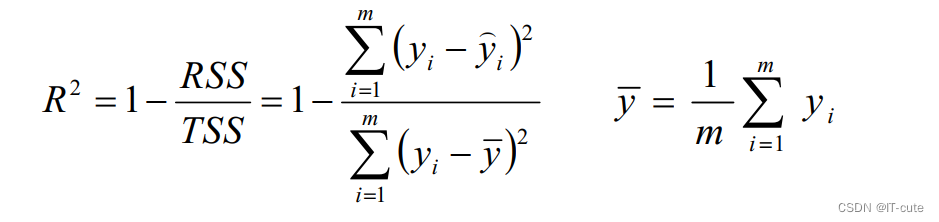
- TSS:总平方和TSS(Total Sum of Squares),表示样本之间的差异情况,是伪方差的m倍
- RSS:残差平方和RSS(Residual Sum of Squares),表示预测值和样本值之间的差异情况,是MSE的m倍
4 机器学习调参
- 在实际工作中,对于各种算法模型(线性回归)来讲,我们需要获取θ、λ、p的值;θ的求解其实就是算法模型的求解,一般不需要开发人员参与(算法已经实现),主要需要求解的是λ和p的值,这个过程就叫做调参(超参)
- 交叉验证:将训练数据分为多份,其中一份进行数据验证并获取最优的超参:λ和p;比如:十折交叉验证、五折交叉验证(scikit-learn中默认)等。
5 梯度下降算法
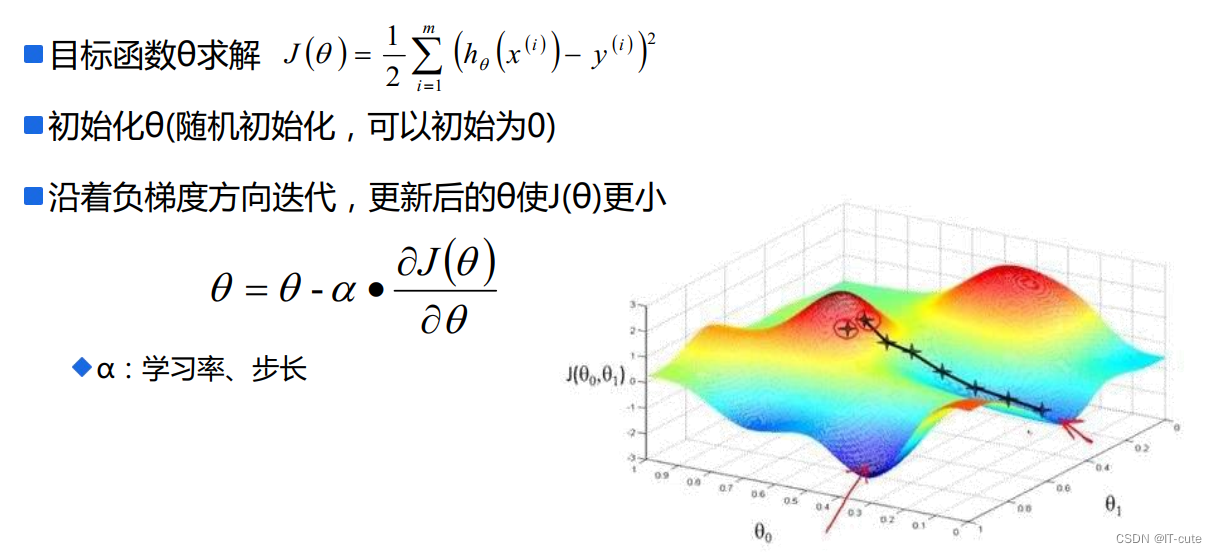
5.1 梯度方向
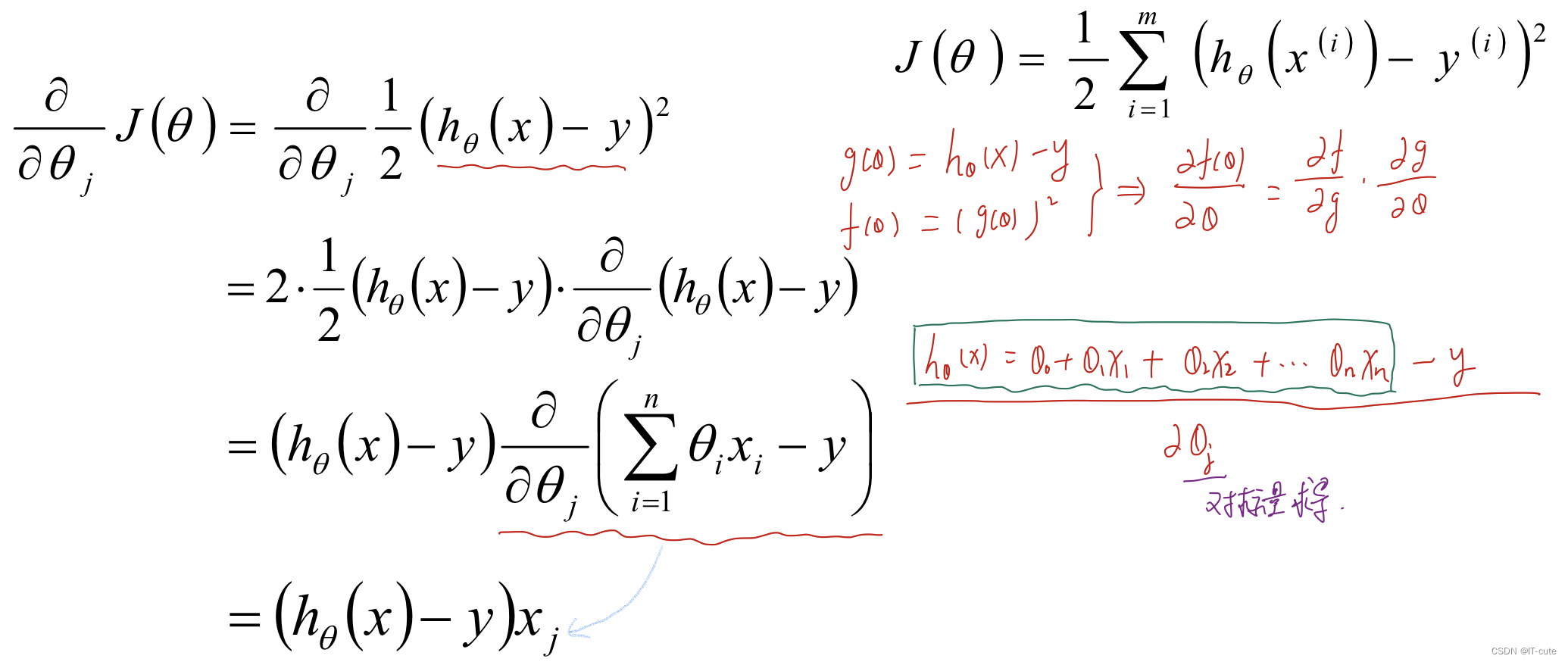
5.2 批量梯度下降算法(BGD)
一次性对m条数据进行操作,m条数据更新一次θ值。
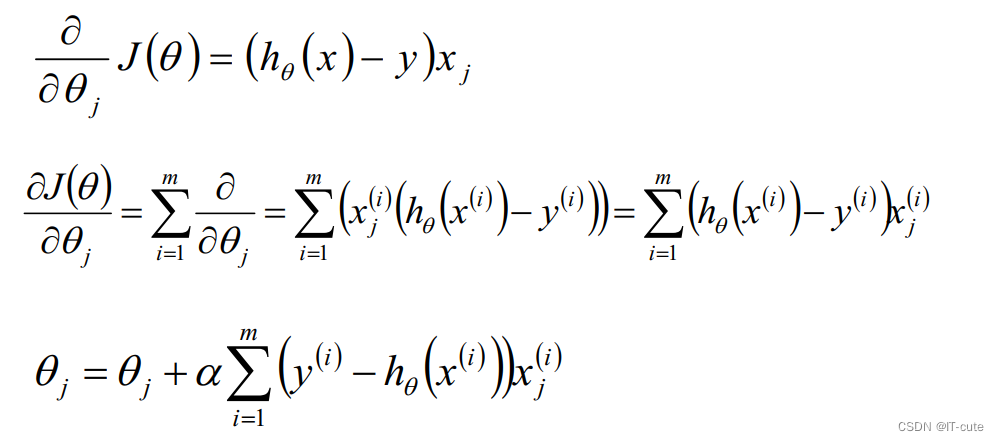
5.3 随机梯度下降算法(SGD)
m条数据更新m次 ,相对来讲,迭代次数更快
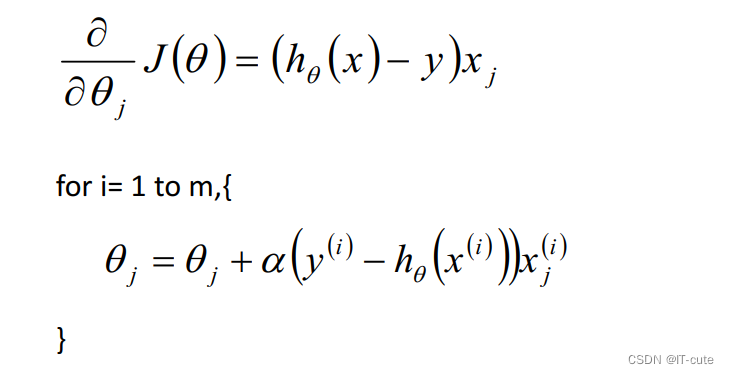
5.4 BGD和SGD算法比较
- SGD速度比BGD快(迭代次数少);
- SGD在某些情况下(全局存在多个相对最优解 / J(θ)不是一个二次),SGD有可能跳出某些小的局部最优解,所以不会比BGD坏;
- BGD一定能够得到一个局部最优解(在线性回归模型中一定是得到一个全局最优解),SGD由于随机性的存在可能导致最终结果比BGD的差;
- 注意:优先选择SGD;
5.5 小批量梯度下降法(MBGD)
如果即需要保证算法的训练过程比较快,又需要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。MBGD中不是每拿一个样本就更新一次梯度,而且拿b个样本(b一般为10)的平均梯度作为更新方向。
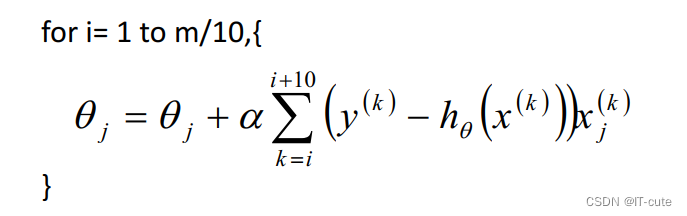
5.6 梯度下降法—调优策略
由于梯度下降法中负梯度方向作为变量的变化方向,所以有可能导致最终求解的值是局部最优解,所以在使用梯度下降的时候,一般需调优策略:
-
学习率的选择:学习率过大,表示每次迭代更新的时候变化比较大,有可能会跳过最优解;学习率过小,表示每次迭代更新的时候变化比较小,就会导致迭代速度过慢,很长时间都不能结束;
-
算法初始参数值的选择:初始值不同,最终获得的最小值也有可能不同,因为梯度下降法求解的是局部最优解,所以一般情况下,选择多次不同初始值运行算法,并最终返回损失函数最小情况下的结果值;
-
标准化:由于样本不同特征的取值范围不同,可能会导致在各个不同参数上送代速度不同,为了减少特征取值的影响,可以将特征进行标准化操作。
5.7 BGD,SGD,MBGD的区别
- 当样本量为m的时候,每次迭代BGD算法中对于参数值更新一次,SGD算法中对于参数值更新m次,MBGD算法中对于参数值更新m/n次,相对来讲SGD算法的更新速度最快;
- SGD算法中对于每个样本都需要更新参数值,当样本值不太正常的时候,就有可能会导致本次的参数更新会产生相反的影响,也就是说SGD算法的结果并不是完全收敛的,而是在收敛结果处波动的;
- SGD算法是每个样本都更新一次参数值,所以SGD算法特别适合样本数据量大的情况以及在线机器学习(Online ML)
6 梯度下降与最小二乘(正规方程)的区别
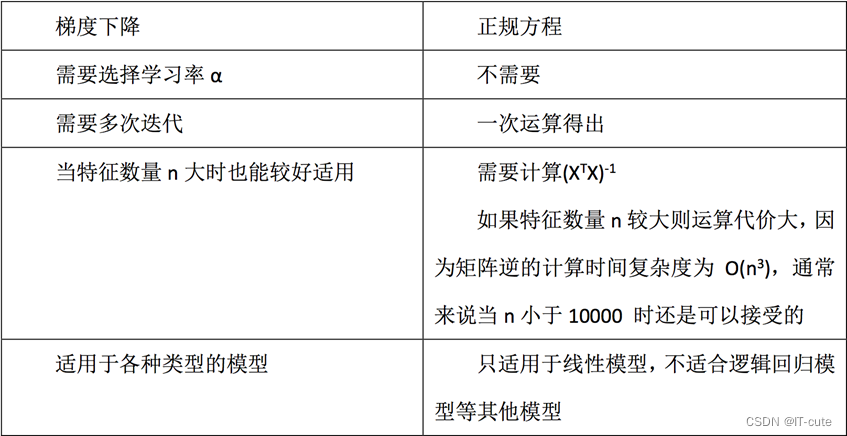
7 用法(梯度下降、坐标轴下降法)
- 只要且标函数是凸函数,就使用梯度下降—>普通的线性回归和L2-norm线性回归
- 坐标轴下降法—>L1-norm
8 线性回归的扩展
- 线性回归针对的是θ而言,对于样本本身而言,样本可以是非线性的
- 也就是说最终得到的函数f:x->y;函数f(x)可以是非线性的,比如:曲线等
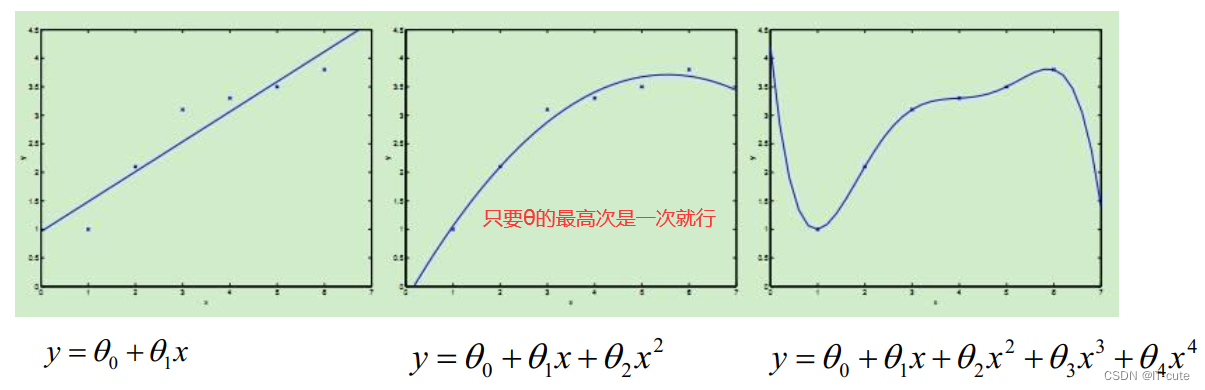
9 线性回归总结

10 局部加权回归—直观理解

10.1 局部加权回归—权重值设置
- w(i)是权重,它根据要预测的点与数据集中的点的距离来为数据集中的点赋权值。当某点离要预测的点越远,其权重越小,否则越大。常用值选择公式为:
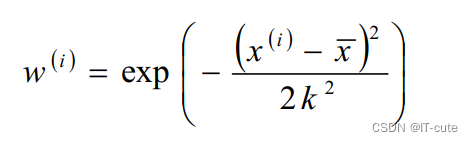
- 该函数称为指数衰减函数,其中k为波长参数,它控制了权值随距离下降的速率
- 注意:使用该方式主要应用到样本之间的相似性考虑,主要内容在SVM中再考虑(核函数)