lambda 函数是 C++ 中的匿名函数,可以内联定义并用作函数对象。 下面是定义 lambda 函数的一般语法:
[capture list] (parameter list) -> return type { function body }
lambda 语法的每个部分:
- `capture list`:这是一个可选的变量列表,lambda 函数可以从周围的上下文中捕获这些变量。 它指定 lambda 函数可以访问和修改哪些变量。
- `parameter list`:这是 lambda 函数采用的以逗号分隔的参数列表。
- `return type`:这是 lambda 函数的返回类型。 它是可选的,如果省略,则返回类型从函数体中的 return 语句推导出来。
- `function body`:这是 lambda 函数的主体。 它包含执行所需操作的代码。
以下是将两个整数相加并返回结果的 lambda 函数示例:
auto add = [](int a, int b) -> int {
return a + b;
};
在此示例中,lambda 函数被分配给变量“add”,它可以像任何其他函数对象一样使用。 我们可以用两个整数调用 add 函数,它会返回两个整数的和。
int sum = add(3, 5); // sum = 8
请注意,“auto”关键字用于推断 lambda 函数的类型,它是一个函数对象。 `-> int` 部分指定 lambda 函数的返回类型是整数。
示例:(leetcode)
1110. 删点成林
给出二叉树的根节点 root,树上每个节点都有一个不同的值。
如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。
返回森林中的每棵树。你可以按任意顺序组织答案。
示例 1:
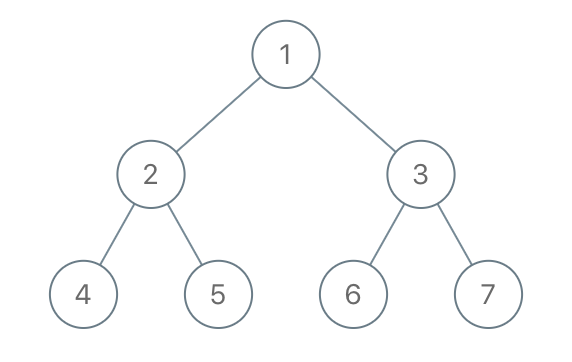
输入:root = [1,2,3,4,5,6,7], to_delete = [3,5] 输出:[[1,2,null,4],[6],[7]]
题解:
/* 思路
题目给定一棵树 root\textit{root}root,树的每个节点都有一个各不相同的值。并且给定一个数组 to_delete\textit{to\_delete}to_delete,包含需要删除的节点值。返回删除所有的 to_delete\textit{to\_delete}to_delete 中的节点后,剩余的树的集合。
可以利用深度优先搜索来遍历每一个节点,定义函数 dfs\textit{dfs}dfs,输入是参数是某个节点 node\textit{node}node 和这个节点是否为潜在的新的根节点 is_root\textit{is\_root}is_root。函数中,首先判断这个节点是否要被删除,如果是,那么它的两个子节点(如果有的话)便成为了潜在的根节点。如果这个节点的值不在 to_delete\textit{to\_delete}to_delete 中并且 is_root\textit{is\_root}is_root 为 true\textit{true}true,那么这个节点便成为了一个新的根节点,需要把它放入结果数组中。同时也要对它的两个子节点进行同样的操作。dfs\textit{dfs}dfs 的返回值为更新后的 node\textit{node}node。
对根节点调用一次 dfs\textit{dfs}dfs,返回新的根节点数组即可。 */
class Solution {
public:
vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
unordered_set<int> to_delete_set(to_delete.begin(), to_delete.end());
vector<TreeNode *> roots;
function<TreeNode *(TreeNode *, bool)> dfs = [&](TreeNode* node, bool is_root) -> TreeNode * {
if (node == nullptr) {
return nullptr;
}
bool deleted = to_delete_set.count(node->val) ? true : false;
node->left = dfs(node->left, deleted);
node->right = dfs(node->right, deleted);
if (deleted) {
return nullptr;
} else {
if (is_root) {
roots.emplace_back(node);
}
return node;
}
};
dfs(root, true);
return roots;
}
};