🍒🍒🍒欢迎关注🌈🌈🌈

📝个人主页：我爱Matlab

👍点赞➕评论➕收藏 == 养成习惯（一键三连）🌻🌻🌻

🍌希望大家多多支持🍓~一起加油 🤗

💬语录：将来的我一定会感谢现在奋斗的自己！

🍁🥬🕒摘要🕒🥬🍁

让我们来想一个特例，80座城市，分布在四个角上，仓库在正中间，总共有四辆车。那么路程最短的解很明显可以想象出是每辆车分别去访问一个角。

使用Matlab用模拟退火（SA）解决VRP问题。首先什么是VRP问题？

大家应该都知道旅行商问题（TSP，Traveling Salesman Problem），即求一个旅行家从一个仓库出发，通过沿途所有城市，再回到仓库所需要的最短路径。TSP问题中只有一个旅行商，那我们如何去解决有多个旅行商(车辆)同时送货的问题呢？

这就引出了VRP问题，即在TSP问题的基础上，加上两个限定条件：

• 有多个旅行商（车辆）同时送货。
• 每个旅行商（车辆）能携带的货物量（capacity）。

也就是说，TSP问题是VRP问题的一个特例（不考虑capacity并且只有一辆车的情况）。

✨🔎⚡运行结果⚡🔎✨

 

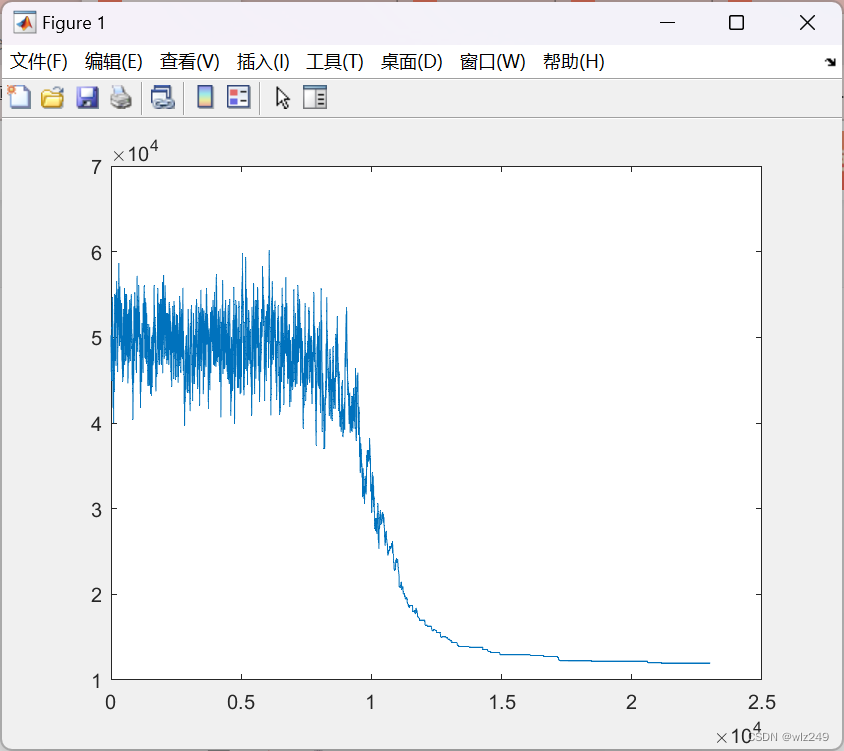
💂♨️👨‍🎓Matlab代码👨‍🎓♨️💂

clc;
clear;
close all;

T0 = 10000000 ; % initial temperature
r = 0.999 ; % temperature damping rate
Ts = 0.001 ; % stop temperature

model = initModel();

% initialization
while(1)
route = randomSol(model);
if(isFeasible(route,model)) 
    break; 
end
end

cost = calculateCost(route,model);
T = T0;
min = cost;

cnt = 1;

% SA
while(T > Ts)
    flag = '#';
    mode = randi([1 3]);
    newRoute = createNeibor(route,model,mode);
    newCost = calculateCost(newRoute,model);
    delta = newCost - cost;
    
    if(delta < 0)
        cost = newCost;
        route = newRoute;
        flag = '*';
    else
        p=exp(-delta/T);
        if rand <= p 
             cost = newCost;
             route = newRoute;
             flag = '^';
        end
    end
    
     if cost < min
         min = cost;
     end
     
     costArr(cnt) = cost;
     
    T = T*r; %  annealing
    disp([flag 'Iteration ' num2str(cnt) ': Best Cost = ' num2str(cost) ' T = ' num2str(T)]);
    cnt = cnt+1;
    
end
disp(min);
plot(costArr);

📜📢🌈参考文献🌈📢📜

"Improvement heuristics for the Vehicle Routing Problem based on Simulated Annealing" —— Alex Van Breedam