一、位图

1.1 位图概念

在计算机的底层，所有的数据都是一段段二进制代码，都只有两个状态0/1，有或无两种状态，而无数个两种状态构成了缤纷多彩的计算机系统。
而位图便是与这种储存方式极其相似的一种数据结构，一般用来记忆、储存、查找。
位图适用于海量数据，通常用来判断某个数据存在与否。
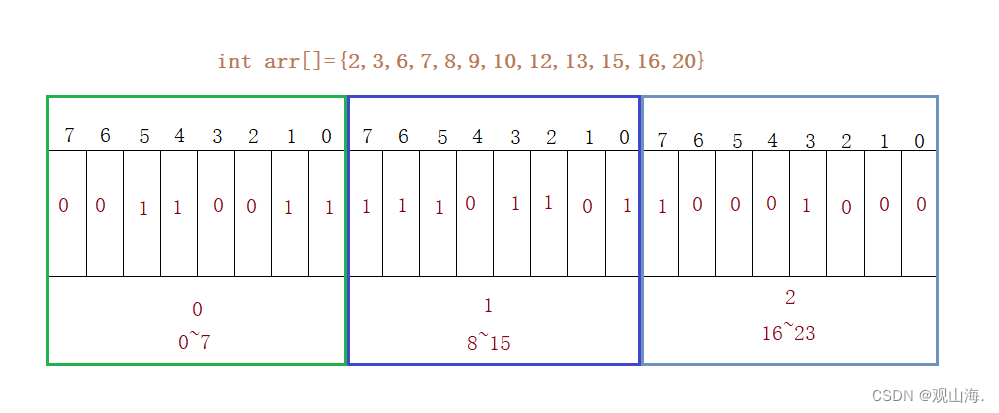
位图：
位图结构仅需要三个数，就可以存储24组信息。
在这里插入图片描述

题目：

1.给40亿个不重复的无符号整数，如何判断某一个具体的数是否在这40亿之中。

我们第一时间想到的是那种解法呢？

遍历查找。
排序，利用二分查找。
位图解决（位图的概念刚好符号这个题目的定义，有或者无）

1.2 位图实现

//初始开辟大小N
template<size_t N>
class bitset
{
public:
	bitset()
	{
		//开辟空间
		_bit.resize(N / 8 + 1, 0);
	}
	void set(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		//将x对应位置一
		_bit[i] |= (1 << j);
	}
	void reset(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		//将x对应位置零
		_bit[i] &= ~(1 << j);
	}
	bool find(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		//查找x对应位是否存在
		return _bit[i] &= (1 << j);
	}
private:
	vector<int> _bit;
	int _bitCount;
};

1.3 单位图的应用方面

快速查询某个数据是否存在。
排序+去重。
求两个巨数集合的交集、并集。
操作系统中磁盘标记号。

二、布隆过滤器

2.1 基本概念

布隆过滤器的提出是为了弥补单位图在某些方面的不足。
布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间。
布隆过滤器就好像一种多映射数据关系，数据的插入与查询等等功能都依托多种映射关系定位。

布隆过滤器映射图：
在这里插入图片描述
就像这样的种种映射关系，一个具体的数字对应位图中多位，来构成多级索引，存储查询。

具体hash关系：

存入张三
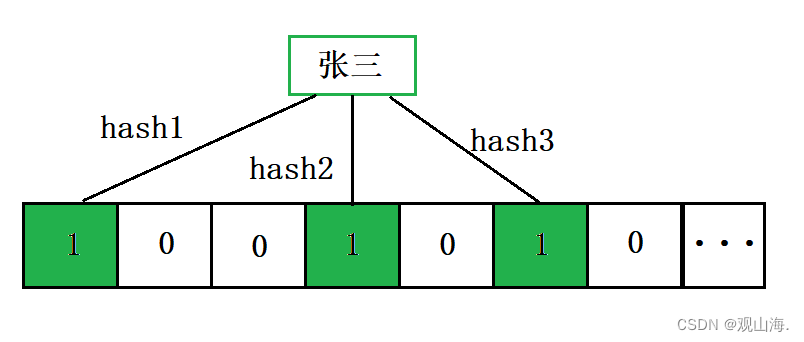
在这里插入图片描述
存入李四

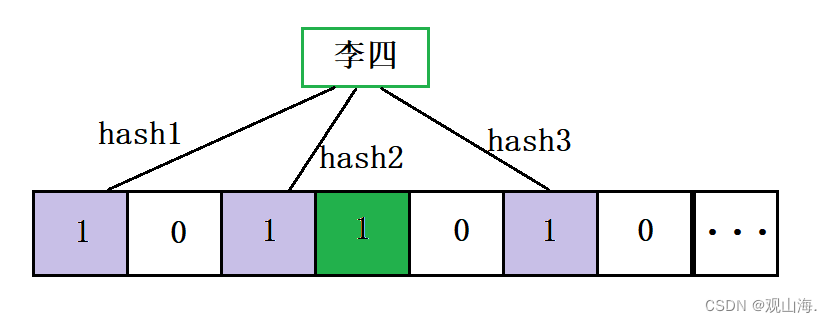
通过图片可以看到他们分别由三中hash关系映射，也有重合的值，但是不完全重合。

2.2 映射关系与代码

代码：

//都是很多权威的大佬研究出的位图中不易重合hash关系映射
//hash映射关系一
struct BKDRHash
{
	size_t operator()(const string& s)
	{
		size_t value = 0;
		for (auto ch : s)
		{
			value *= 31;
			value += ch;
		}
		return value;
	}
};
//hash映射关系二
struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
			}
		}
		return hash;
	}
};
//hash映射关系三
struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};

进入映射：

//不同的映射template
template<size_t N,
	size_t X = 5,
	class K = string,
	class HashFunc1 = BKDRHash,
	class HashFunc2 = APHash,
	class HashFunc3 = DJBHash>
	class BloomFilter
{
public:
	void Set(const K& key)
	{
		//空间
		size_t len = X * N;
		//计算三种hash关系值index
		size_t index1 = HashFunc1()(key) % len;
		size_t index2 = HashFunc2()(key) % len;
		size_t index3 = HashFunc3()(key) % len;
		//位图记录
		_bs.set(index1);
		_bs.set(index2);
		_bs.set(index3);
	}
	bool Test(const K& key)
	{
		//查找是否存在，单存在一定误判（极少）
		size_t len = X * N;
		size_t index1 = HashFunc1()(key) % len;
		if (_bs.test(index1) == false)
			return false;
		size_t index2 = HashFunc2()(key) % len;
		if (_bs.test(index2) == false)
			return false;
		size_t index3 = HashFunc3()(key) % len;
		if (_bs.test(index3) == false)
			return false;
		return true;  // 存在误判的
	}
	// 不支持删除，删除可能会影响其他值。
	void Reset(const K& key);
private:
	bitset<X* N> _bs;
};

2.3 布隆过滤器的查找与删除

删除：
首先布隆过滤器不支持删除，因为每个存入值并非一一对应关系，删除就预示着存在误删情况。
查找：
同时布隆过滤器的查找并非精确查找，有概率出现误差，布隆过滤器可以理解为一种粗略查找方式。
但是如果确定某一个数不存在于布隆过滤器中那就一定不在布隆过滤器中，但如果该数存在却又是一种不确定存在，因为哈希函数有一定程度的误判。