一、Logistic回归原理

1、Sigmoid函数作用

Logistic回归的原理是用逻辑函数把线性回归的结果(-∞,+∞)映射到(0,1)，下面介绍线性回归函数和逻辑函数。

• 线性回归函数
  线性回归函数的数学表达式:
  $$y={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2,+\dots +{\theta }_n{x}_n={\theta }^{T}x$$
  其中xi是自变量，y是因变量，y的值域为(-∞,+∞)，${\theta }_0$是常数项，${\theta }_i$是待求系数，不同的权重${\theta }_i$反映了自变量对因变量不同的贡献程度。
  对于一元一次方程: y=a+bx，这种只包括一个自变量和一个因变量的回归分析称为一元线性回归分析。
  对于二元一次方程: y= a+b1x1+b2x2，三元一次方程: y = a+b1x1+b2x2+b3x3，这种回归分析中包括两个或两个以上自变量的回归分析，称为多元线性回归分析。
  不管是一元线性回归分析还是多元线性回归分析，都是线性回归分析。

• Sigmoid函数
  函数表达式：
  $$g(z)=\frac{1}{1+e^{-z}}$$
  函数图像：
  
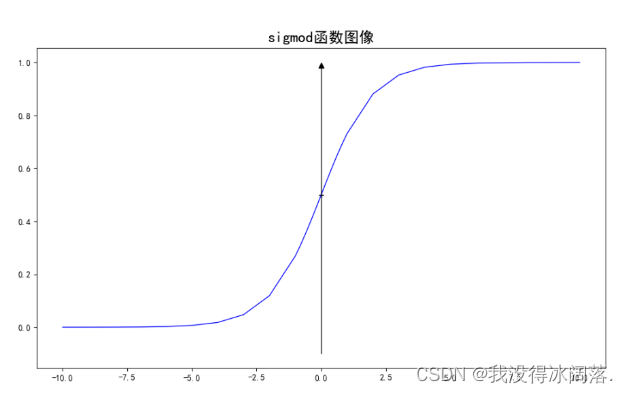
  从图像中可以看出，当z趋于-∞，g(z)趋于0，当z趋于+∞，g(z)趋于1，且函数的值阈为(0,1)。原理是当z趋于-∞，$e^{-z}$趋于∞，g(z)趋于0，当z趋于+∞，$e^{-z}$趋于0，g(z)趋于1。
  同时可以发现当z趋于5时，g(z)的值已经到0.99附近，z越大，g(z)越趋于1。所以这个函数很好描述我们日常生活中，平时碰到的概率。我们可能认为明天下雨的概率为0.3，天晴的概率为0.7。抛一枚硬币正面的概率为0.5，反面的概率也为0.5。概率也是介于0到1之间的一些数，很自然我们可以把sigmod函数的值域和概率联系起来。

2、用梯度下降法求解参数

梯度下降过程类似一个人下山过程：

• step1:明确自己现在所处的位置;
• step2:找到现在所处位置下降最快的方向;
• step3:沿着第二步找到的方向走一个步长，到达新的位置，且新位置低于刚才的位置;
• step4:判断是否下山，如果还没有到最低点继续步骤—，如果已经到最低点，则停止。

从上面的分析知，用梯度下降法求解参数最重要的是找到下降最快的方向和确定要走的步长。
那么什么是函数下降最快的方向?
如果学过一元函数的导数，应该知道导数的几何意义是某点切线的斜率。除此之外导数还可以表示函数在该点的变化率，导数越大，表示函数在该点的变化越大。

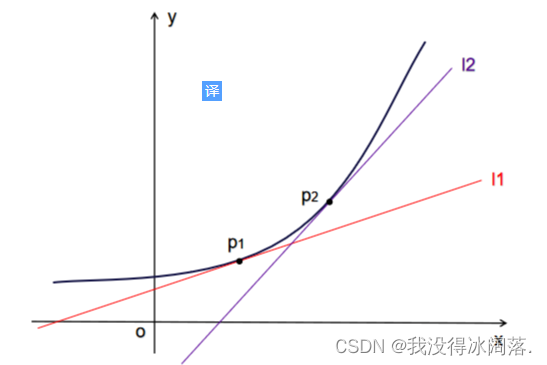
从图中可以发现p2点的斜率大于p1点的斜率，即p2点的导数大于p1点的导数。对于多维向量
$$x=(x_1,x_2,...,x_n)$$
它的导数叫做梯度(偏导数)，当求某个变量的导数时，把其它变量视为常量，对整个函数求导，也就是分别对于它的每个分量求导数，即
$$x^{{}^{\prime }}=(x_1^{{}^{\prime }},x_2^{{}^{\prime }},...,x_n^{{}^{\prime }})$$
对于函数的某个特定点，它的梯度就表示从该点出发，函数值变化最为迅猛的方向。至此梯度下降法求解参数的方向已经找到，那就是函数的梯度方向。

二、利用Logistic回归分类

1、数据预处理

1. 获取数据集
   我的数据集是获取用户个人信息（年龄、教育情况、工龄、地址、收入、负债率、银行卡负债等情况），利用这些信息，最后判断用户是否违约。
   
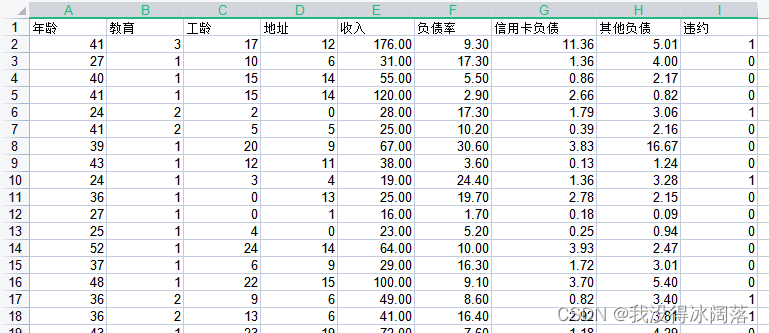
   预处理时，先将用户信息存入一个二维数组中，其返回值data_arr 为数据特征，label_arr是每个数据对应标签 ：

def load_data_set(fileName):
    data_arr = []
    label_arr = []
    f = open(fileName, 'r')
    for line in f.readlines():
        line_arr = line.strip().split()
        data_arr.append([np.float(line_arr[0]), 
                            np.float(line_arr[1]),
                            np.float(line_arr[2]),
                            np.float(line_arr[3]),
                            np.float(line_arr[4]),
                            np.float(line_arr[5]),
                            np.float(line_arr[6]),
                            np.float(line_arr[7])])
        label_arr.append(int(line_arr[8]))
    data_arr = maxminnorm(data_arr)
    return data_arr, label_arr
data_arr, class_labels = load_data_set()

在预处理时要注意如果有的数据太大，要将数据归一化，如果不归一化会导致数据溢出。根据sigmoid函数
$$g(z)=\frac{1}{1+e^{-z}}$$当z过大时，$e^{-z}$数值是很大的，所以要将器归一化处理，根据归一化公式： $$x_i=\frac{x_i-min(x)}{max(x)-min(x)}$$根据公式可以将数据全部保证在0-1之间，并且不丢失数据代表的特征。带入到sigmoid函数后，就不会有数据溢出的异常了。

def maxminnorm(array):
    array = np.array(array)
    maxcols=array.max(axis=0)
    mincols=array.min(axis=0)
    data_shape = array.shape
    data_rows = data_shape[0]
    data_cols = data_shape[1]
    t=np.empty((data_rows,data_cols))
    for i in range(data_cols):
        t[:,i]=(array[:,i]-mincols[i])/(maxcols[i]-mincols[i])
    return t

2、利用梯度上升计算回归系数

• 梯度上升模型
  梯度上升法，其实就是因为使用了极大似然估计，传入的就是一个普通的数组param data_arr，当然你传入一个二维的ndarray也行。class_labels 是类别标签，它是一个的行向量。为了便于矩阵计算，需要将该行向量转换为列向量，做法是将原向量转置，再将它赋值给label_mat。

def grad_ascent(data_arr, class_labels):
    data_mat = np.mat(data_arr)
    # 变成矩阵之后进行转置
    label_mat = np.mat(class_labels).transpose()
    # m->数据量，样本数 n->特征数
    m, n = np.shape(data_mat)
    # 学习率，learning rate
    alpha = 0.001
    # 最大迭代次数
    max_cycles = 500
    # 生成一个长度和特征数相同的矩阵
    # weights 代表回归系数， 此处的 ones((n,1)) 创建一个长度和特征数相同的矩阵，其中的数全部都是 1
    weights = np.ones((n, 1))
    for k in range(max_cycles):
        h = sigmoid(data_mat * weights)
        error = label_mat - h
        weights = weights + alpha * data_mat.transpose() * error
    return weights

• 随机梯度上升算法：
  梯度上升算法在更新回归系数是都要遍历整个数据集，如果处理的样本数和标签数太多，那计算的复杂度就太大了。如果一次只用一个样本点来更新回归系数，这种方法叫做随机梯度上升算法。随机梯度上升算法和梯度上升算法区别有：（1）后者的变量和误差都是向量，而前者全是数值；（2）前者没有矩阵转换过程，所有变量都是numpy数组。

def stoc_grad_ascent0(data_mat, class_labels):
    m, n = np.shape(data_mat)
    alpha = 0.01
    weights = np.ones(n)
    for i in range(m):
        # sum(data_mat[i]*weights)为了求 f(x)的值， f(x)=a1*x1+b2*x2+..+nn*xn,
        # 此处求出的 h 是一个具体的数值，而不是一个矩阵
        h = sigmoid(sum(data_mat[i] * weights))
        error = class_labels[i] - h
        weights = weights + alpha * error * data_mat[i]
    return weights

• 改进随机梯度上升算法：
  相对于随机梯度上升算法，这个算法改进了几个方面：（1）aplha在每次迭代的时候都会调整，这会缓解数据波动。另外，虽然aplha会随着迭代次数不断减少，但永远不会减少到0；（2）通过随机选取样本更新回归系数，这种方法减少波动；（3）可以修改默认的迭代次数，第三个参数可以将迭代次数传入，没有默认为150次。

def stoc_grad_ascent1(data_mat, class_labels, num_iter=150):
    m, n = np.shape(data_mat)
    weights = np.ones(n)
    for j in range(num_iter):
        # 这里必须要用list，不然后面的del没法使用
        data_index = list(range(m))
        for i in range(m):
            # i和j的不断增大，导致alpha的值不断减少，但是不为0
            alpha = 4 / (1.0 + j + i) + 0.01
            # 随机产生一个 0～len()之间的一个值
            # random.uniform(x, y) 方法将随机生成下一个实数，它在[x,y]范围内,x是这个范围内的最小值，y是这个范围内的最大值。
            rand_index = int(np.random.uniform(0, len(data_index)))
            h = sigmoid(np.sum(data_mat[data_index[rand_index]] * weights))
            error = class_labels[data_index[rand_index]] - h
            weights = weights + alpha * error * data_mat[data_index[rand_index]]
            del(data_index[rand_index])
    return weights

3、训练和验证

• 最终分类函数
  根据回归系数和特征向量来计算 Sigmoid 的值，大于0.5函数返回1，否则返回0

def classify_vector(in_x, weights):
    # print(np.sum(in_x * weights))
    prob = sigmoid(np.sum(in_x * weights))
    if prob > 0.5:
        return 1.0
    return 0.0

• 训练模型

def colic_test():
    f_train = open('data/loandata.txt', 'r')
    f_test = open('data/loandata_test.txt', 'r')
    training_set = []
    training_labels = []
    # trainingSet 中存储训练数据集的特征，trainingLabels 存储训练数据集的样本对应的分类标签
    for line in f_train.readlines():
        curr_line = line.strip().split('\t')
        if len(curr_line) == 1:
            continue    # 这里如果就一个空的元素，则跳过本次循环
        line_arr = [float(curr_line[i]) for i in range(8)]
        training_set.append(line_arr)
        training_labels.append(float(curr_line[8]))
    # 使用 改进后的 随机梯度下降算法 求得在此数据集上的最佳回归系数 trainWeights
    train_weights0 = grad_ascent(np.array(training_set), training_labels)
    train_weights1 = stoc_grad_ascent0(np.array(training_set), training_labels)
    train_weights2 = stoc_grad_ascent1(np.array(training_set), training_labels)
    error_count0 = 0
    error_count1 = 0
    error_count2 = 0
    num_test_vec = 0.0
    # 读取 测试数据集 进行测试，计算分类错误的样本条数和最终的错误率
    for line in f_test.readlines():
        num_test_vec += 1
        curr_line = line.strip().split('\t')
        if len(curr_line) == 1: 
            continue    # 这里如果就一个空的元素，则跳过本次循环
        line_arr = [float(curr_line[i]) for i in range(8)]
        if int(classify_vector(np.array(line_arr), train_weights0)) != int(curr_line[8]):
            error_count0 += 1
        if int(classify_vector(np.array(line_arr), train_weights1)) != int(curr_line[8]):
            error_count1 += 1
        if int(classify_vector(np.array(line_arr), train_weights2)) != int(curr_line[8]):
            error_count2 += 1
    right_rate = 1 - (error_count0 / num_test_vec)
    print('梯度下降法正确率：{}'.format(right_rate))
    right_rate = 1 - (error_count1 / num_test_vec)
    print('随机梯度下降法正确率：{}'.format(right_rate))
    right_rate = 1 - (error_count2 / num_test_vec)
    print('改进随机梯度下降法正确率：{}'.format(right_rate))
    return 

运行结果：

总结

• 在进行数据预处理时注意归一化
  数据集中，如果有相当一部分数据值太大，经过sigmoid函数计算导致溢出。归一化处理后，所有数据都在0与1之间，并且能够保留数据代表的特征。不进行归一化处理，对sigmoid函数优化也能解决这个问题。
• 梯度下降算法优势
  在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。
• 改进的随机梯度上升算法
  相对于随机梯度上升算法，这个算法改进了几个方面：（1）aplha在每次迭代的时候都会调整，这会缓解数据波动。另外，虽然aplha会随着迭代次数不断减少，但永远不会减少到0；（2）通过随机选取样本更新回归系数，这种方法减少波动；（3）可以修改默认的迭代次数，第三个参数可以将迭代次数传入，没有默认为150次。