第一节：线性表的顺序表示

线性表

1. 定义

由n(n>=0)个相同类型的元素组成的有序集合。

L=(a1,a2,……,ai-1,ai,ai+1,……,an)

• 线性表中元素个数n，称为线性表的长度。当n=0时，为空表。
• a1是唯一的“第一个”数据元素，an是唯一的“最后一个”数据元素。
• ai-1为ai的直接前驱，ai+1为ai的直接后继。

2. 特点

• 表中元素的个数是有限的。
• 表中元素的数据类型都相同。意味着每一个元素占用相同大小的空间。
• 表中元素具有逻辑上的顺序性，在序列中各元素排序有其先后顺序。

线性表的顺序表示

1. 顺序表

逻辑上相邻的两个元素在物理位置上也相邻。

顺序表的定义：

#define MaxSize 50  // 定义线性表的长度
typedef struct{
    ElemType data[MaxSize]; // 顺序表的元素
    int len;   // 顺序表的当前长度
}SqList;  // 顺序表的类型定义

2. 优缺点比较

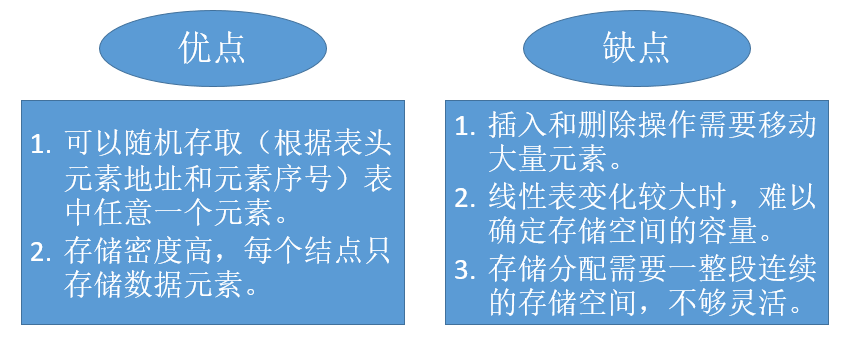
3. 插入操作

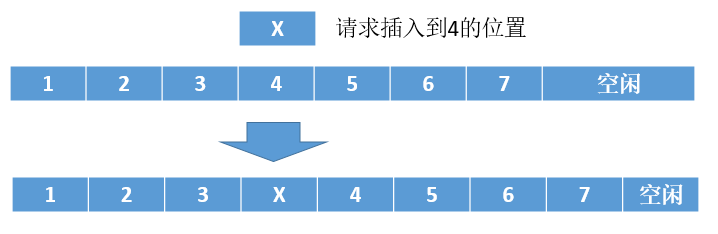
分析：

最好情况：在表尾插入元素，不需要移动元素，时间复杂度为O(1)。

最坏情况：在表头插入元素，所有元素依次后移，时间复杂度为O(n)。

平均情况：在插入位置概率均等的情况下，平均移动元素的次数为n/2，时间复杂度为O(n)。

代码片段

// 判断插入位置i是否合法（满足1<=i<=len+1）
// 判断存储空间是否已满（即插入X后是否会超出数组长度）
for(int j=L.len;j>=i;j--){
    L.data[j]=L.data[j-1]; // 将最后一个元素到第i个元素依次后移一位
}
L.data[i-1]=x;  // 空出的位置i除放入x
L.len++;  // 线性表长度加1

说明：我们在实际的操作中下标是从0开始的，但是说的第几个元素时从1开始的。第i个元素，下标实际为i-1。

4. 删除操作

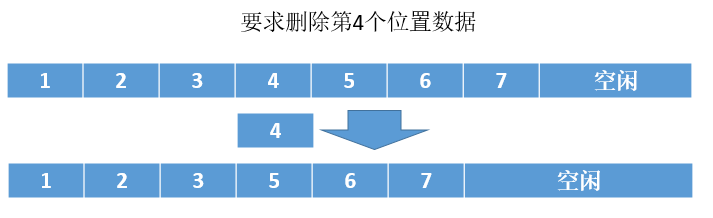
分析：

最好情况：删除表尾元素，不需要移动任何元素，时间复杂度为O(1)。

最坏情况：删除表头元素，之后的所有元素依次前移，时间复杂度为O(n)。

平均情况：在删除位置概率均等的情况下，平均移动元素的次数为(n-1)/2，时间复杂度为O(n)。

代码片段

// 判断删除位置i是否合法（满足1<=i<=len）
e=L.data[i-1];  // 将被删除的元素赋值给e
for(int j=i;j<L.len;j++){
    L.data[j-1]=L.data[j];  // 将删除位置后的元素依次前移
}
L.len--;  // 线性表长度减1

说明：我们在实际的操作中下标是从0开始的，但是说的第几个元素时从1开始的。第i个元素，下标实际为i-1。

5. 动态分配

#define InitSize 100  // 表长度的初始定义
typedef struct{
    ElemType *data;  // 指示动态分配数组的指针
    int MaxSize,length;  // 数组的最大容量和当前个数
}SeqList;  // 动态分配数组顺序表的类型定义

C的初始动态分配语句为：

L.data=(ElemType*)malloc(sizeof(ElemType)*InitSize);

C++的初始动态分配语句为：

L.data=new ElemType[InitSize];

代码示例

#include <stdio.h>

#define MaxSize 50
typedef int ElemType;
// 静态分配
typedef struct {
    ElemType data[MaxSize];
    int len;  // 当前顺序表中元素个数
}SqList;

// 插入
// i表示插入的位置，从1开始，e要插入的元素
bool ListInsert(SqList &L,int i,ElemType e){
    if(i<1 || i>L.len+1){  // 判断插入位置是否合法
        return false;
    }
    if(L.len>=MaxSize){  // 判断存储空间是否已满
        return false;
    }
    for(int j=L.len;j>=i;j--){ // 移动顺序表中的元素
        L.data[j]=L.data[j-1];
    }
    L.data[i-1]=e;
    L.len+=1; // 添加一个元素，顺序表元素加1
    return true;
}

// 删除
// i表示删除的位置，从1开始。使用元素e的引用的目的是拿出对应的值
bool ListDel(SqList &L,int i,ElemType &e){
    if(i<1 || i>L.len){ // 判断删除的位置是否合法
        return false;
    }
    e=L.data[i-1]; // 获取顺序表中对应的元素，赋值给e
    for (int j=i;j<L.len;j++) {
        L.data[j-1]=L.data[j];
    }
    L.len-=1; // 删除一个元素，顺序表长度减1
    return true;
}

// 查找
// 查找成功，返回位置，位置从1开始，查找失败，返回0。e表示要查找的元素，这里不考虑重复元素
int ListFind(SqList L,ElemType e){
    for(int i=0;i<L.len;i++){
        if(L.data[i]==e){
            return i+1;  // 加1就是元素在顺序表中的位置
        }
    }
    return 0;
}

// 修改
// i表示修改的位置，e表示修改后的值
bool ListUpdate(SqList &L,int i,ElemType e){
    if(i<1 || i>L.len){ // 判断修改的位置是否合法
        return false;
    }
    L.data[i-1]=e;
    return true;
}

// 打印线性表
void PrintList(SqList L){
    for(int i=0;i<L.len;i++){
        printf("%3d",L.data[i]);
    }
    printf("\n");
}
int main() {
    printf("init Linear table\n");
    SqList L; // 顺序表的名称
    bool ret;
    L.data[0]=1;
    L.data[1]=2;
    L.data[2]=3;
    L.len=3;  // 总计3个元素
    printf("insert Linear table element\n");
    ret=ListInsert(L,2,50);
    if(ret){
        printf("success\n");
        PrintList(L);
    } else{
        printf("failed\n");
    }
    printf("delete Linear table element\n");
    ElemType del;
    ret= ListDel(L,1,del);
    if(ret){
        printf("success\n");
        PrintList(L);
    } else{
        printf("failed\n");
    }
    printf("find Linear table element\n");
    int result;
    result=ListFind(L,2);
    if(result != 0){
        printf("success\n");
        printf("position is %d\n",result);  // 打印元素位置
    } else{
        printf("failed\n");
    }
    printf("update Linear table element\n");
    ret= ListUpdate(L,2,18);
    if(ret){
        printf("success\n");
        PrintList(L);
    } else{
        printf("failed\n");
    }
    return 0;
}

F:\Computer\Project\practice\10\10.1-linear_table\cmake-build-debug\10_1_linear_table.exe
init Linear table
insert Linear table element
success
  1 50  2  3
delete Linear table element
success
 50  2  3
find Linear table element
success
position is 2
update Linear table element
success
 50 18  3

进程已结束，退出代码为 0

第二节：线性表的链式表示

单链表

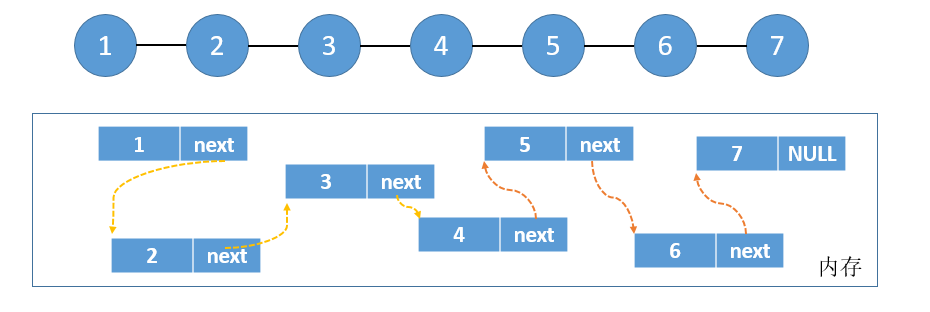
逻辑上相邻的两个元素在物理位置上不相邻。

单链表结点的定义：

typedef struct LNode{ // 单链表结点类型
    ElemType data;  // 数据域
    struct LNode *next;  // 指针域
}LNode,*LinkList;

头指针：链表中第一个节点的存储位置，用来标识单链表。

头结点：在单链表第一个节点之前附加的一个结点，为了操作上的方便。

若链表有头结点，则头指针永远指向头结点，不论链表是否为空，头指针均不为空，头指针是链表的必须元素，它标识一个链表。

头结点是为了操作的方便而设立的，其数据域一般为空，或者存放链表的长度。有头结点后，对在第一结点前插入和删除第一结点的操作就统一了，不需要频繁重置头指针。但头结点不是必须的。

优缺点对比

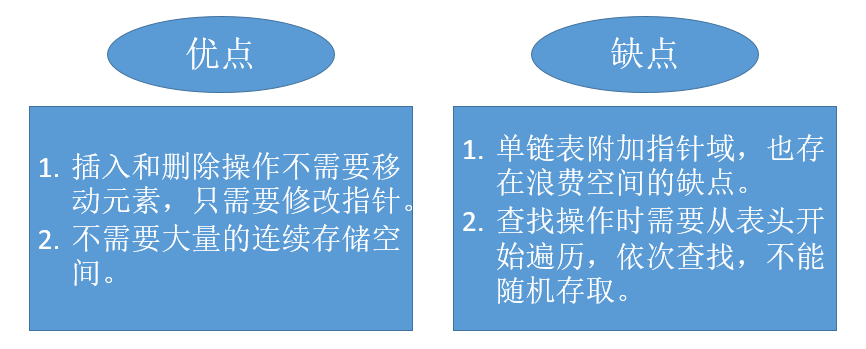
插入操作

创建新结点

q=(LNode*)malloc(sizeof(LNode))
q->data=x;

头插入和中间插入

q->next=p->next;
p->next=q;

尾插入

p->next=q;
q->next=NULL;

说明：q是新插入的元素。p是指针指向的元素。

删除操作

p=GetElem(L,i-1); // 查找删除位置的前驱结点
p->next=q->next;
free(q);

说明：q是要删除的元素，p是指针指向的元素。删除完后要释放空间。

代码示例

按序号查找结点值的算法如下：

LNode *p=L->next;
int j=1;
while(p && j<i){
    p=p->next;
    j++;
}
return p;

按值查找结点的算法如下：

LNode *p=L->next;
while(p!=NULL && p->data!=e){
    p=p->next;
}
return p;

说明：L是头指针，用来指向头结点。