有效的井字游戏

难度：中等

给你一个字符串数组 $board$ 表示井字游戏的棋盘。当且仅当在井字游戏过程中，棋盘有可能达到 $board$ 所显示的状态时，才返回 $true$ 。

井字游戏的棋盘是一个 3 x 3 数组，由字符 ' '，'X' 和 'O' 组成。字符 ' ' 代表一个空位。

以下是井字游戏的规则：

• 玩家轮流将字符放入空位（' '）中。
• 玩家 1 总是放字符 'X' ，而玩家 2 总是放字符 'O' 。
• 'X' 和 'O' 只允许放置在空位中，不允许对已放有字符的位置进行填充。
• 当有 3 个相同（且非空）的字符填充任何行、列或对角线时，游戏结束。
• 当所有位置非空时，也算为游戏结束。
• 如果游戏结束，玩家不允许再放置字符。

示例 1：

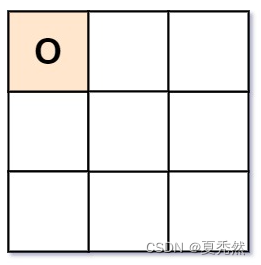
输入：board = ["O  ","   ","   "]
输出：false
解释：玩家 1 总是放字符 "X" 。

示例 2：

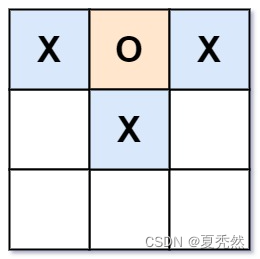
输入：board = ["XOX"," X ","   "]
输出：false
解释：玩家应该轮流放字符。

示例 3:

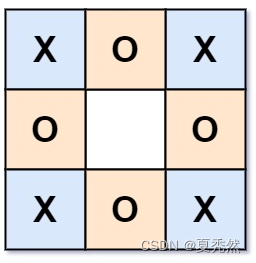
输入：board = ["XOX","O O","XOX"]
输出：true

分类讨论

思路：
题目要求判断当前游戏板是否生效，我们思考游戏板生效的规则：

• 玩家轮流将字符放入空位 $\text{" "}$ 中。第一个玩家总是放字符 $\text{"X"}$，且第二个玩家总是放字符 $\text{"O"}$。因为第一个玩家总是先手，这就要求游戏板中字符 $\text{"X"}$ 的数量一定是大于等于字符 $\text{"O"}$ 的数量。
• $\text{"X"}$ 和 $\text{"O"}$ 只允许放置在空位中，不允许对已放有字符的位置进行填充。
• 当有 $3$ 个相同（且非空）的字符填充任何行、列或对角线时，游戏结束。当所有位置非空时，也算为游戏结束。如果游戏结束，玩家不允许再放置字符，不可能能出现二者同时获胜的情况，因此游戏板上不可能同时出现 $3$ 个 $\text{"X"}$ 在一行和 $3$ 个 $\text{"O"}$ 在另一行。
• 获胜的玩家一定是在自己放棋后赢得比赛，赢得比赛后，立马停止放置字符。
  • 如果第一个玩家获胜，由于第一个玩家是先手，则次数游戏板中 $\text{"X"}$ 的数量比 $\text{"O"}$ 的数量多 $1$。
  • 如果第二个玩家获胜，则 $\text{"X"}$ 的数量与 $\text{"O"}$ 的数量相同。

以上条件包含了游戏板生效的全部情况，可以通过反证法验证上面分类条件的正确性。在合法的游戏板，只能有 $3$ 种结果合法，要么没有任何玩家赢，要么玩家一赢，要么玩家二赢。我们可以通过检查两种棋的数量关系即可验证是否有效，同时我们要检测是否存在两个玩家同时赢这种非法情况。

算法实现细节如下:

• 首先统计游戏板上 $\text{"X"}$ 和 $\text{"O"}$ 的数量并记录在 $\text{xCount}$ 和 $\text{oCount}$ 中，如果不满足 $\text{xCount}\ge \text{oCount}$，则此时为非法，直接返回 $\text{false}$。
• 然后我们检查是否有玩家是否获胜，我们检查在棋盘的 $3$ 行，$3$ 列和 $2$ 条对角线上是否有该玩家的连续 $3$ 枚棋子。我们首先检测玩家一是否获胜，如果玩家一获胜,则检查 $\text{xCount}$ 是否等于 $\text{oCount}+1$；我们继续检测玩家二是否获胜，如果玩家二获胜，则检查 $\text{xCount}$ 是否等于 $\text{oCount}$。
• 对于特殊情况如果两个玩家都获胜，是否可以检测出该非法情况？如果同时满足两个玩家都获胜，则 $\text{"X"}$ 和 $\text{"O"}$ 数量的合法的组合可能为 $(3,3),(4,3),(4,4),(5,4)$，对于 $(3,3),(4,4)$ 不满足玩家一获胜的检测条件，对于 $(4,3),(5,4)$ 满足玩家一获胜的检测条件但不满足玩家二的获胜条件。

时间复杂度： $O(C)$，由于此题给定的棋盘大小为常数 $C=9$，因此时间复杂度为常数。
空间复杂度： $O(1)$。

class Solution:
    def win(self, char, board):
        return any(board[0][i] == char and board[1][i] == char and board[2][i] == char or
                   board[i][0] == char and board[i][1] == char and board[i][2] == char for i in range(3)) or \
                   board[0][0] == char and board[1][1] == char and board[2][2] == char or \
                   board[2][0] == char and board[1][1] == char and board[0][2] == char
    def validTicTacToe(self, board: List[str]) -> bool:
        ocount = sum(row.count("O") for row in board)
        xcount = sum(row.count("X") for row in board)
        return not (xcount - ocount not in [0, 1] or
                   xcount - ocount != 0 and self.win('O', board) or
                   xcount - ocount != 1 and self.win('X', board))

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/valid-tic-tac-toe-state